基于簇负荷特性曲线的“聚类-回归”电力大用户短期负荷预测

任 勇， 曾 鸣

(1.华北电力大学 经济与管理学院 北京 102206;2.贵州电网有限责任公司， 贵州 贵阳 550002)

0 引 言

近年来，随着我国电力行业的不断发展与革新[1-5]，电力用户用电模式日趋多元化与智能化[6]，为用户提供更好的用电服务是构建泛在电力物联网的核心内容[7-9]。电力大用户一般是指钢铁、矿石、冶炼、商业等高耗能产业用户，对电力大用户进行负荷预测具有重大理论和现实意义：从用户的角度而言，目前很多厂矿企业不仅仅在线路入厂处装设电能计量装置，在车间内部也有电能监测计量装置[10]，可以实现设备能耗、电流、功率因数等的实时监控，企业内部形成电能管理系统，负荷预测可以帮助大用户高效管理企业用电情况、淘汰旧设备、合理安排生产计划；从电力公司的角度而言，在工业区和商业区负荷中，占比较高的大用户负荷波动会显著影响变电站以及附近区域的总体负荷状况[11-13]，对大用户进行准确的负荷预测可以有效预防大用户负荷波动对电网带来的冲击，及早对网架结构进行针对性的优化，提高供电可靠性。同时，电力负荷预测对于泛在电力物联网中用户用电感知起到支撑的作用[14]。

学者们对大用户用电特性及负荷特性展开了深入研究，文献[15]讨论了区块链技术在大用户直购电方面的应用，并从市场准入、交易、结算和物理约束4个方面阐述了应用细则；文献[16]从多个角度对大用户直购电展开分析，给出了在国内推广大用户直购电的制度设计与建议；文献[17]分析了考虑风电消纳的大用户用电负荷特征；类似地，文献[18,19]分析了消纳风电的大用户在电力系统调度中的模型构建。

负荷预测是一个历久弥新的课题，文献[20,21]以综述的形式较全面地总结了传统的负荷预测方法，比如：时间序列法、相似日法、灰色预测法、专家系统法等；近年来，基于机器学习算法的新兴负荷预测方法受到越来越多的关注，文献[22]中提出了一种基于逻辑回归(logistic regression, LR)的配网负荷预测预警方法，文献[23]中提出了基于改进的支持向量机回归(support vector machine regression, SVR)的短期负荷预测方法，文献[24]提出了基于内存运算平台spark的L2-Boosting回归方法，在负荷预测方面取得了良好效果，文献[25,26]中分别在两种平台上利用分布式文件存储系统(HDFS)对海量数据进行存储和运算，通过对决策树(Cart)算法进行集成(ensemble)，实现了并行随机森林算法(random forest, RF)。

这些机器学习算法的共同特点是属于浅层学习(shallow learning)模型[27]，即模型在结构上可以看成带有一层隐藏层(hidden layer)节点，比如SVR、Boosting，或者没有隐藏层节点，比如LR。浅层模型的局限在于有限样本下对复杂函数的表示能力不足，容易产生过拟合，模型泛化能力差。深度学习(deep learning)可以弥补这些不足，深度神经网络含有多个隐藏层，特征学习能力强，在相同训练集下，深度学习可以比浅层学习得到“更有用”的特征[28]，由于含有多个隐藏层，所以可以用较少的参数表示复杂函数，通过深层非线性网络实现对复杂函数的逼近。

文献[29]提出了一种基于进化深度学习特征提取模型的短期负荷预测方法，比传统负荷预测方法有更高负荷预测精度。文献[30]将深度长短时记忆网络应用于超短期负荷预测的场景，并通过参数优化寻求最适合该网络的超参数。文献[31]提出了一种自适应深度信念网络，并应用于220 kV变电站出线负荷预测；文献[32]则将频域分解与深度学习方法相结合，并对光伏电站出力进行了预测。

本文在总结前人工作的基础上提出了一种基于簇负荷特性曲线的“聚类-回归”电力大用户短期负荷预测方法。该方法首先对电力大用户按照用电特征聚类，用电特征相似的用户聚为一簇，提出了“簇负荷特性曲线”的概念来描述簇内用户的用电水平，最后将不同簇的簇负荷曲线作为总负荷的属性因子来训练深度神经网络模型模型。在TensorFlow深度学习框架下实现了“聚类-回归”模型，通过我国西南某省电力大用户的实际用电数据设计实验，验证了“聚类-回归”模型的准确性和有效性。

1 “聚类-回归”短期负荷预测模型

下面介绍基于簇负荷特性曲线的“聚类-回归”电力大用户短期负荷预测方法。

1.1 分布式TensorFlow框架

TensorFlow是谷歌(Google)公司开源的深度学习计算框架，该框架很好地支持包括深度学习在内的多种算法[33]。

TensorFlow分为单机模式和分布式模式两种，单机模式指客户端(client)、管理节点(driver)、工作节点(worker)均在一台机器的同一进程中，client是TensorFlow中的重要组成部分，client通过session接口与driver和多个worker相连，每个worker又与多个硬件设备相连并管理CPU或者GPU，driver则负责所有worker按流程执行计算图(computation graph)；分布式模式则允许client、driver、worker在不同机器的进程中，由集群调度系统统一管理。本项目组采用的是TensorFlow的分布式模式。

1.2 基于簇负荷特性曲线的“聚类-回归”电力大用户短期负荷预测模型

本文提出的基于簇负荷特性曲线的“聚类-回归”电力大用户短期负荷预测模型流程如图1所示。

1.2.1 数据预处理

数据清洗与预处理的目的是筛去坏数据与明显错误的数据、补全缺失数据，同时对样本数据进行归一化，便于程序处理。待处理的部分原始数据如表1所示。表格中的总、峰、平、谷分别表示对应用户在一天之内的总有功电量，高峰时段有功电量，平常时段有功电量，以及低谷时间有功电量。无功表示无功电量，最大功率表示一天内出现的最大有功负荷，倍率表示实际数据与通过互感器采集数据之间的比率。

表1 大用户用电特征数据样例Tab.1 Samples of power consumption characteristic data of large users

在对大用户进行用电特征聚类时考虑的属性有总电量、峰电量、平电量、谷电量以及最大功率。为了方便程序处理，增加不同用户之间的可比较性，对上述原始数据进行了归一化处理处理，得到更加直观体现用电特征的4个属性属性：峰总比、平总比、谷总比、负荷率。定义如式(1)～式(4)所示：

(1)

(2)

(3)

(4)

式中：r1为峰总比；r2为谷总比；r3为平总比；η为负荷率；Loverall为总电量；Lpeak为峰电量；Lvalley为谷电量；Lflat为平电量；Pmax为最大功率。

1.2.2 电力大用户聚类

根据式(1)～式(4)四个属性对用户进行聚类。可采用的聚类算法有多种，k均值聚类(k-means)是最为经典的一种方法，如表2所示。

表2 k-means算法Tab.2 K-means algorithm

初始聚类中心可以通过随机选择或者人工指派来实现。通过tf.constant()函数把数据转换为常量tensor，tf.random_shuffle()函数对数据随机化，tf.slice()函数可以从原始数据中抽取部分维度来研究。tf.Variable()函数将初始聚类中心从常量转化为变量。

接下来需要计算样本到聚类中心的距离，距离的度量一般有：

(1)n维空间中两个点x和y之间的欧氏距离(Euclidean distance)，表达式如下：

(5)

式中：n为空间的维数；xk和yk分别为x和y的第k个属性(第k个分量)。

(2)将欧氏距离推广，可以得到更为一般的明科夫斯基距离(Minkowski distance):

(6)

式中：r为参数，通过对r的不同取值，可以得到不同的范数意义下的距离：

r=1时的距离称为曼哈顿距离(Manhattan distance)或者汉明距离(Hamming distance)，此时的距离表示为x和y之间的L1范数：

(7)

r=2时为数学上的L2范数，同式(5)；

r=∞时，为无穷范数距离(L∞-distance)，为样本属性之间的最大的距离，表示为式(8)：

(8)

以欧式距离为例，在TensorFlow中通过tf.expand_dims()函数扩充变量维度，tf.sub()函数实现变量的减法，tf.square()函数实现对分量平方。tf.reduce_sum()函数计算样本点到聚类中心距离之和，tf.argmin()函数返回距离值最小的聚类中心的标号。

聚类的目标即聚类中心不发生变化，或者变化很小，可以用SSE (sum of the squared error, SSE)来衡量，通过计算每个数据点到聚类中心的欧氏距离，迭代计算误差的平方和，SSE越小，聚类效果越好，SSE计算式如下：

(9)

(10)

式中：x为样本；Ci为第i个簇；ci为簇Ci的质心；mi为第i个簇中样本的数目；K为簇的个数，dist(ci,x)为对应的聚类中心ci与相应的簇内的样本x的距离。对于簇Ci，采用tf.equal()函数标记样本点是否属于该簇， tf.gather()函数按标记抽取属于该簇的样本，tf.reduce_mean()函数计算簇Ci的新的聚类中心ci。不断迭代，直到满足收敛条件。

1.2.3 簇负荷特性曲线

通过对电力大用户聚类，得到表征簇内用户用电水平的簇负荷曲线，为下一步构建负荷预测模型做准备，用电特征类似的用户聚为一个簇，经过多次实验，对于本项目中的数据，簇的个数取20。对于簇Ci中的ni个用户，根据式(11)，可得到C条簇负荷曲线。

(11)

式中：Load(i)是簇Ci的簇负荷曲线向量，96维，簇负荷曲线向量元素为lj，lj为簇Ci所包含的用户在第j时刻的负荷均值。

簇负荷曲线表征了用电特征类似的一类用户的负荷水平。采用k-means算法得到的簇负荷曲线如图2所示。

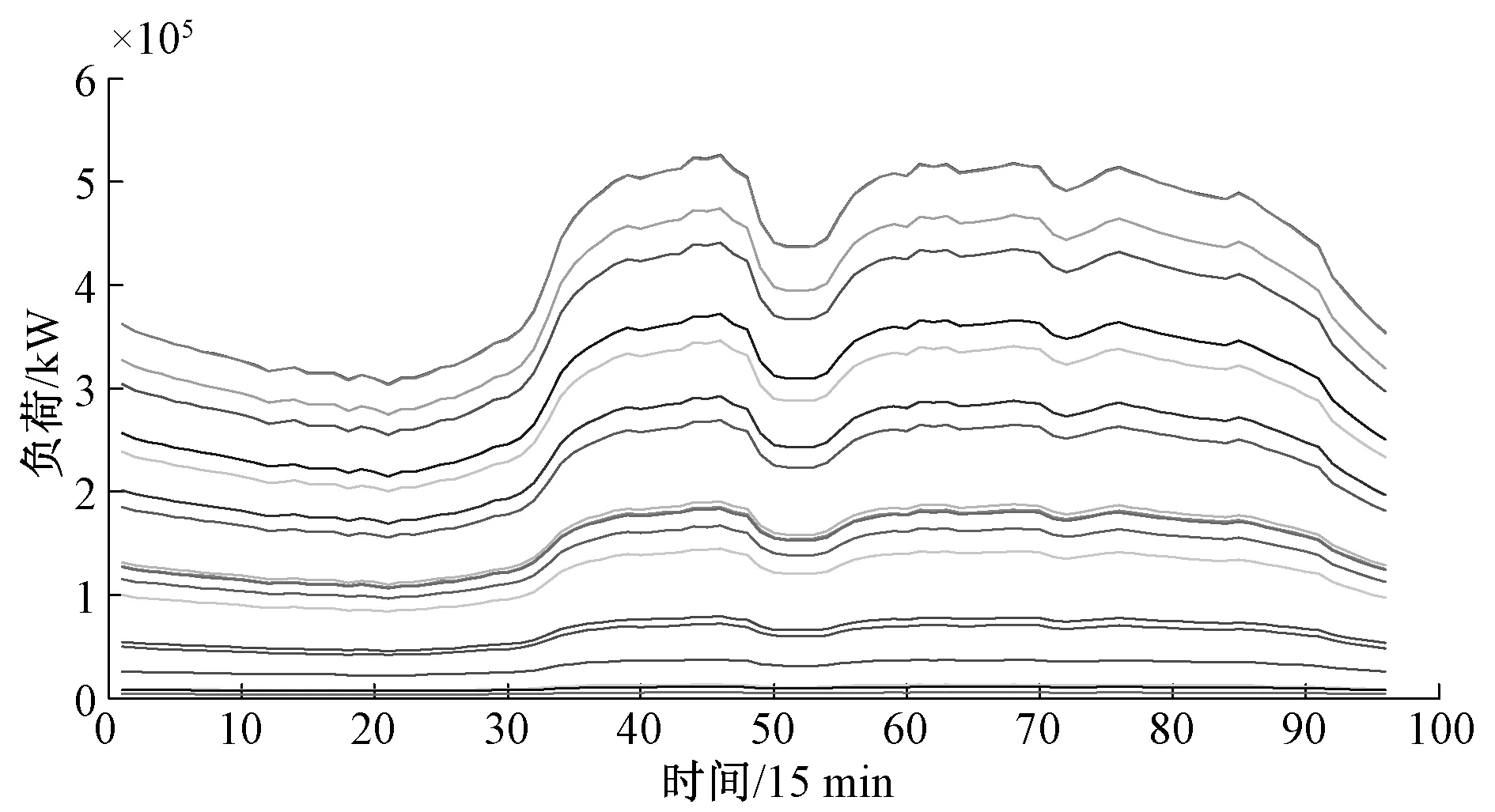
图2 区域大用户的簇负荷曲线Fig.2 Cluster load curve of regional large users

1.2.4 回归预测

回归预测的算法也有多种，本文以TensorFlow框架下长短期记忆网络(long short term memory, LSTM)为例来进行回归预测。

长短期记忆网络属于循环神经网络(recurrent neural network,RNN)的一种。如图3所示，循环神经网络在每一个时刻都会有一个输入xt，结合循环神经网络当前的状态At，得到输出ht。而当前的状态At是上一时刻的状态At-1和当前的输入xt共同作用决定的，这种结构很适合解决与时间序列相关的问题。

图3 RNN网络结构框图Fig.3 RNN network structure diagram

然而太长的时间序列会导致当前节点对历史节点的感知能力不足，出现梯度消散(vanish of gradient)问题。同时，当前预测和所需信息之间的跨度长短不一，这种长期依赖(long-term dependencies)问题是传统循环神经网络不能解决的。

LSTM对经典循环神经网络做了改进，通过引入“遗忘门”，让信息有选择性地影响RNN中每个时刻的状态，如图4所示。“遗忘门”与“输入门”是LSTM的核心结构，遗忘门通过当前的输入xt和上一时刻的输出ht-1，对上一时刻状态ct-1中的元素设置权重，权重取值范围从0到1。如式(12)所示。

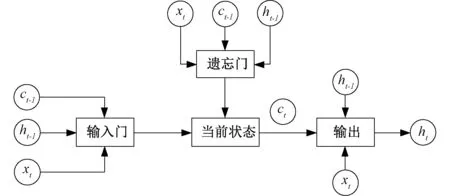
图4 LSTM网络结构框图Fig.4 LSTM network structure diagram

f1=σ(Wf·[ht-1,xt]+bf)

(12)

式中：Wf为遗忘门的权重矩阵；bf为偏置项，[ht-1,xt]为遗忘门的输入向量；σ为sigmoid函数。新状态的补充由“输入门”完成，输入门根据，ht-1决定ct-1状态的哪些部分写入当前时刻的状态ct中去。如式(13)所示。

it=σ(Wi·[ht-1,xt]+bi)

(13)

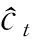
(14)

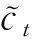
(15)

类似地，输出门表示如式(16)所示。

ot=σ(Wo·[ht-1,xt]+bo)

(16)

而LSTM最终的输出ht是由输出门与单元状态共同决定的，如式(17)所示。

ht=ot·tanh(ct)

(17)

TensorFlow中可以直接调用函数tf.nn.rnn()实现LSTM。结合前一步得到的簇负荷特性曲线作为实际负荷的属性因子就可以训练模型，进而进行负荷预测。

2 算例分析

2.1 实验平台搭建

课题组搭建了基于TensorFlow框架的分布式电力大数据平台，如图5所示，采用4台ThinkServer TD350服务器作为worker节点，1台ThinkServer TD350服务器作为driver节点。Worker节点机器配置了双核CPU，主频2.94 GHz，内存16G，硬盘1TB，操作系统为Linux Ubuntu 16.04 desktop；driver节点配置了4核CPU，主频2.60 GHz，内存32 GB，硬盘10TB，操作系统为Linux Ubuntu 16.04 desktop。集群开发用到的开源软件版本如下：Hadoop 2.7.3，Spark 2.0.1，jdk 1.8，Scala 2.11.8，Python 2.7。

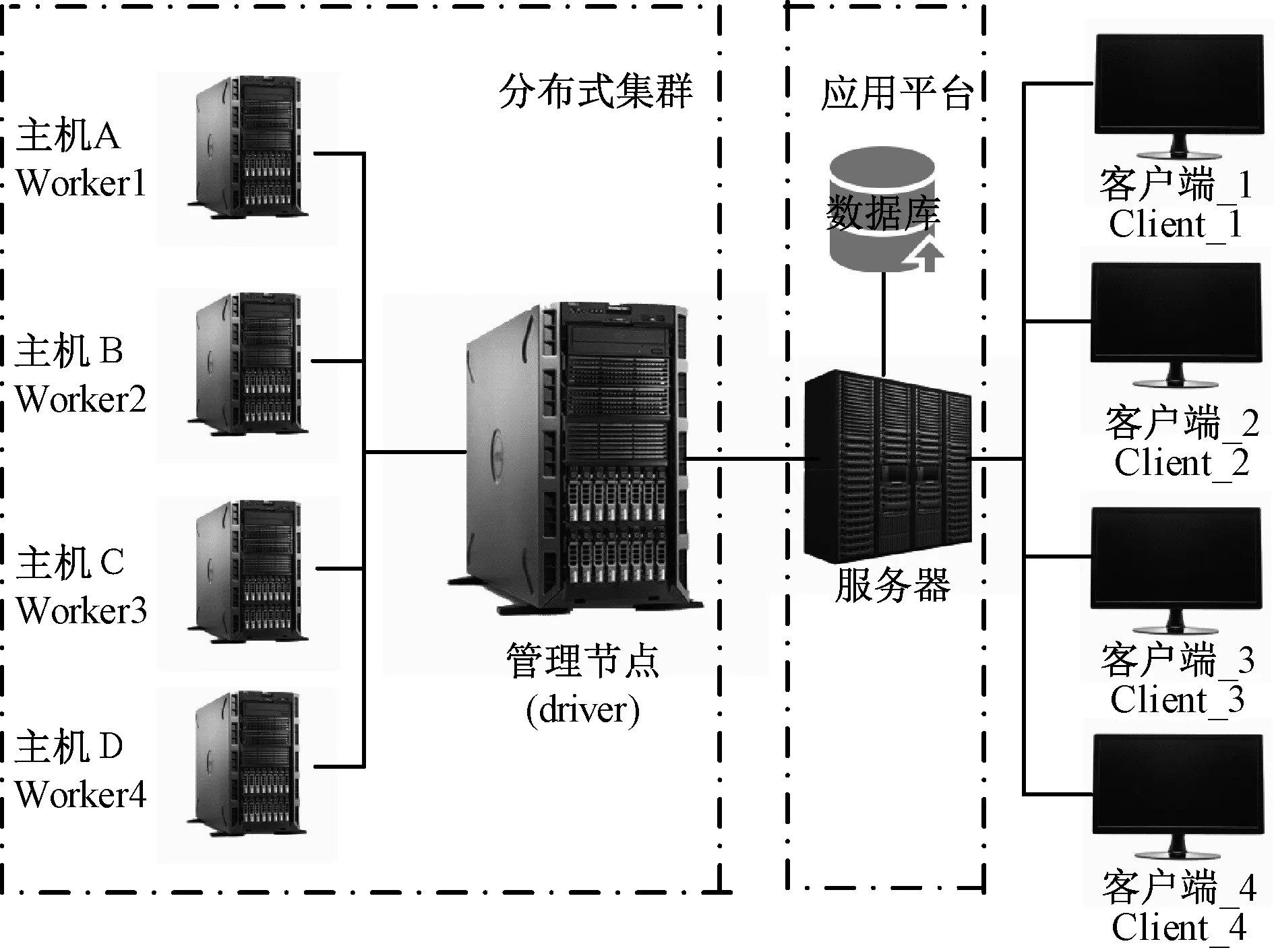
图5 分布式集群拓扑Fig.5 Distributed cluster topology

2.2 实验数据介绍

实验所用的“大用户用电特征数据”以及“区域负荷数据”均来自我国西部某电力公司，“区域负荷数据”记录了每15 min的区域用户负荷值(kW)，数据由计量自动化系统自动采集。预测误差的评价采用了平均百分误差(mean absolute percentage error, MAPE)和均方根误差(root-mean-square error, RMSE)，计算公式如下:

(18)

(19)

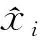
2.3 实验设计与分析

2.3.1 实验1：考察“聚类-回归”负荷预测模型的准确性

将本文提出的“聚类-回归”负荷预测模型与传统的不经过“聚类”直接“回归”的负荷预测模型进行预测结果比较。其中，“聚类-回归”模型的聚类阶段采用kmeans算法，回归阶段采用LSTM算法。将kmeans-LSTM方法与传统的LSTM回归预测方法进行比较。以研究区域的2016年7月1日至2017年6月30日的负荷数据作为训练集，对2017年7月1日的负荷数据进行预测。预测结果如图6所示。

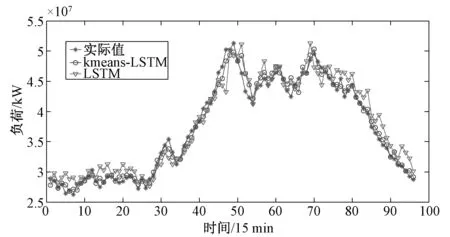
图6 “聚类-回归”模型与传统模型预测精度比较Fig.6 Comparison of prediction accuracy between “clustering regression” model and traditional model

按照式(18)、(19)计算两种方法的MAPE与RMSE如表3所示。

表3 “聚类-回归”模型与传统模型预测误差统计Tab.3 Prediction error statistics of cluster regression model and traditional model

图7为两种方法在每个计量点的百分误差曲线。

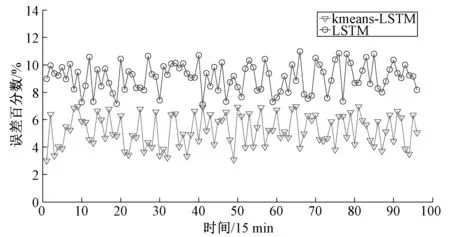
图7 “聚类-回归”模型与传统模型百分误差比较Fig.7 Percentage error comparison between “clustering regression” model and traditional model

通过图6、图7以及表3的误差统计可以看出“聚类-回归”负荷预测模型比传统的直接回归预测模型有更高的负荷预测精度。“聚类-回归”模型中通过聚类将区域内用电特征类似的用户聚为一簇，得到表征簇内用户一般化用电水平的“簇负荷特性曲线”(如图2)，不同的簇负荷曲特性线代表了该研究区域负荷的不同组成成分，将簇负荷特性曲线作为负荷预测分析的属性因子，就是从更细粒化的角度分析区域负荷的构成，从而在负荷预测中将区域内用户的用电特征均有所体现，达到进一步提高负荷预测精度的目的。

2.3.2 实验2：“聚类-回归”模型(kmeans-LSTM)的参数优化

深度学习模型中参数的设置对模型训练的有效性和重构误差率(reconstruction error rate, RER)影响很大，下面针对对影响“聚类-回归”模型(kmeans-LSTM)的三个主要参数进行优化。

(1)学习率调整

合适的学习率策略可以显著提高深度学习模型的收敛速度，缩短模型的训练时间。为了对比不同学习策略下kmeans-LSTM模型的性能，本文选择了4种常见的学习策略进行实验，即常数型、AdaMix、AdaGrad和RMSProp。通过对比不同学习率策略下模型的RER和模型迭代时间，得到最适合本文模型的学习策略。在相同的迭代次数下，RER越小算法收敛效果越好，RER计算如式(20)所示。

(20)

式中：RMSE(l)为第l组实验数据集的均方根误差。

模型RER比较如图8所示，可以看出，不同策略下kmeans-LSTM模型RER随迭代次数的增加而减小，逐步趋于稳定。在整个迭代过程中，模型学习策略采用常数型、AdaGrad型和RMSProp型的RER相对接近，AdaMix型的重构误差曲线在迭代次数为150次后完全优于另外3种；模型学习策略采用常数型、AdaGrad型、RMSProp型的最终RER分别为8.67、8.64、8.73，而模型学习策略采用AadMix型RER为8.27。实验结果表明AdaMix型学习策略相比其它3种策略收敛效果更好。

图8 不同学习率策略的重构误差对比Fig.8 Comparison of reconstruction errors of different learning rate strategies

kmeans-LSTM模型采用4种学习策略迭代550次所耗时间如表4所示。

表4 “聚类-回归”模型(kmeans-LSTM)在不同学习策略下的迭代时间Tab.4 Iteration time of “clustering regression” model (k-means LSTM) under different learning strategies

模型采用常数型学习率的迭代时间最短，之后依次是AdaMix型，AdaGrad型和RMSProp型。相同迭代次数下，模型采用AadMix型学习率比采用常数型学习率的运算时间更长，但从图8可看出两种学习率方法达到相同的收敛效果时，基于常数型学习率的模型需要迭代更多的次数。

AdaMix型学习率调整策略在充分考虑模型参数特点的基础上，为权重设计了更能反映模型运行状态的学习率，为偏置设计了收敛速度好且计算量较小的幂指数函数，使得模型中不同类型的参数能够依据自身的状态实现快速收敛。综合考虑重构误差率和模型迭代时间，选择AadMix型作为kmeans-LSTM模型的学习率策略。

(2)激活函数

激活函数的引入可以有效解决RNN中梯度消散问题，提高模型鲁棒性。不同的激活函数为模型提供不同的选择空间，对模型学习能力的提升也不同。

本次实验针对kmeans-LSTM模型选用了3种常见的激活函数做对比：sigmoid函数、ReLU(rectified linear unit)函数、softplus函数。考察在不同激活函数下kmeans-LSTM模型负荷预测的平均准确度(mean accuracy, mAcc)，表5、如式(21)所示。

表5 不同激活函数下负荷预测平均准确度Tab.5 Average accuracy of load forecasting under different activation functions

(21)

式中各符号的意义同式(18)。

从表5中可以看出，kmeans-LSTM模型采用softplus激活函数时mAcc最高，且迭代时间最短，优于基于sigmoid函数和ReLU函数的模型。这是因为对于softplus类型的激活函数，其导函数有相对更宽广的定义域取到较大函数值，且softplus的导函数较ReLU的导函数更为平滑。因此相比ReLU函数和sigmoid函数，softplus函数可以为神经网络提供更大的可选择空间，有效地提高模型学习能力。

(3)dropout参数

dropout参数的设置可以有效抑制神经网络训练的过拟合。dropout的原理是在模型训练时，以一定的概率让某个神经元失活，在TensorFlow中通过tf.nn.dropout()函数实现。目前学术界对dropout的取值方法并无定论，具体到本文模型，采用遍历的方法选取最优值。

本文尝试了10种不同的dropout比例，实验结果如图9所示。

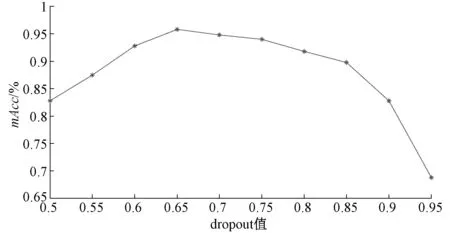
图9 不同dropout参数下负荷预测平均准确度Fig.9 Average accuracy of load forecasting under different dropout parameters

当dropout参数从0.5增大至0.95，mAcc呈现了先增加后减小的变化趋势，在dropout取0.67时mAcc获得最大值0.958。

2.3.3 实验3：“聚类-回归”模型在分布式环境下与单机环境下的压力测试

考虑到“聚类-回归”模型应用于分布式集群环境，故设计一组压力实验，考察随着实验数据的递增，kmeans-LSTM分别在分布式环境下和单机环境下运行，处理相同规模的样本所消耗的时间。

分布式集群的配置如2.1节所述，运行kmeans-LSTM的单机配置了双核CPU，主频2.94 GHz，内存4G。两种环境下每次训练相同的数据集，统计两种环境下kmeans-LSTM在每个数据集上的运行时间。

实验结果如表6和图10所示。其中在单机环境下处理950 MB数据时机器出现内存溢出错误。

从表6和图10可以看出，当数据集规模较小时(小于750 MB)单机模型优势明显，分布式集群消耗时间较长，这是因为集群中driver给worker分配任务、设备调配需要消耗一定的时间，而这部分时间消耗在单机中是不需要的。随着数据量的增加，大于550 MB后分布式环境下模型的运行时间趋于稳定；而单机模型随着数据量增加所消耗时间成倍增长，从图10可以看出，在数据量为750 MB时两种环境下消耗时间基本持平，数据量为850 MB时，kmeans-LSTM在单机环境下运行时间超过分布式环境下运行的时间，当数据量大于950 MB时，单机环境已无法正常进行运算。

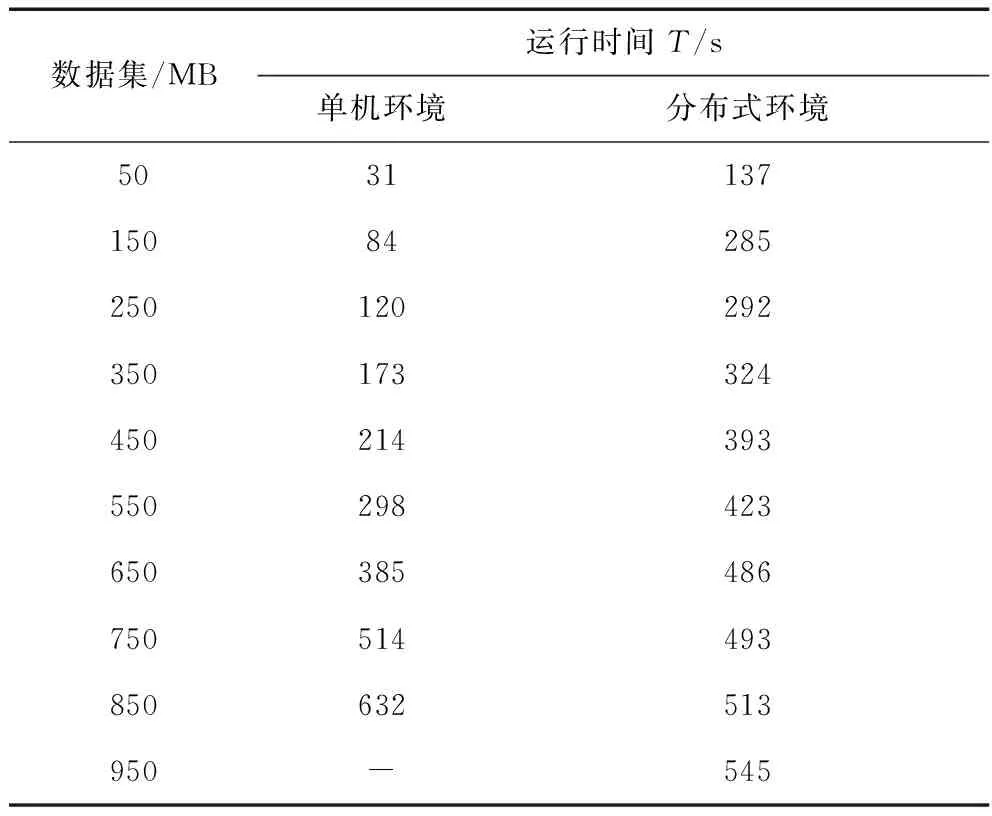
表6 模型在分布式环境与单机环境的运行时间Tab.6 Running time of model in distributed environment and single machine environment

图10 “聚类-回归”负荷预测模型在分布式环境与单机环境运行时间对比Fig.10 Comparison of running time of “cluster regression” load forecasting model in distributed environment and single machine environment

由此可见，本文提出的“聚类-回归”负荷预测模型可以很好地适应分布式环境，随着数据量的递增，分布式环境下模型运行优势明显。

3 结 论

本文在总结前人工作的基础上提出了一种基于簇负荷特性曲线分析的“聚类-回归”电力大用户短期负荷预测方法。首先通过聚类的方法对区域用户负荷进行细粒度的分析，将用电特征类似的用户聚为一簇，提出了代表簇内用户一般化用电水平的“簇负荷特性曲线”的概念，将簇负荷特性曲线作为区域负荷属性因子建立模型进行负荷预测。以实际数据设计实验，得到如下结论：

(1)在聚类阶段采用kmeans算法，回归阶段采用LSTM算法，在TensorFlow深度学习框架下实现了“聚类-回归”(kmeans-LSTM)模型。本文所提方法与传统的不经聚类，直接回归预测的LSTM方法相比，在MAPE、RMSE两项误差统计指标占优，验证了本文所提方法的准确性；

(2)针对本文的“聚类-回归”模型(kmeans-LSTM)进行了参数优化。AdaMix型学习率调整策略对权重与偏置的设置更为合理，模型参数能够实现较快收敛，通过实验验证了模型采用softplus型激活函数可以得到更高的负荷预测平均准确度，具体到本文模型，dropout参数值设置为0.67时，可以得到最大的负荷预测平均准确度0.958；

(3)在分布式环境下对“聚类-回归”模型进行了阶梯数据集压力测试，随着数据量的增加，“聚类-回归”模型在大规模数据集上运算性能稳定。与单机方法相比，分布式环境下的“聚类-回归”负荷预测模型能够更好地适应当前电力大数据环境，验证了本文所提方法的有效性。