变压器双层多线声源等效模型的建立与研究

郭兆枫， 倪园， 陈传敏， 张建功

(1.华北电力大学 环境科学与工程学院 河北省燃煤电站烟气多污染物协同控制重点实验室，河北 保定 071003； 2.华北电力大学 区域能源系统优化教育部重点实验室，北京 102206； 3.中国电力科学研究院有限公司，湖北 武汉 430074)

0 引 言

随着国民经济水平的提高，全社会用电量持续增加。特高压变电站的建设随之增多，从而引发的噪声污染问题也越来越显现[1, 2]。目前，造成工程投运后噪声超标问题的主要原因，就是无法有效在规划设计阶段准确的预测噪声[3-13]。使用SoundPLAN等商业噪声预测软件对变电站的声环境进行预测计算是目前常用的方法，但其有着建模过程过于程序化，无法有效进行干涉衍射计算，无法针对变电站的具体情况进行相应修正的缺点。周亚琪[14]等人对某变压器噪声信号进行全相快速傅里叶变换(fast Fourier transform，FFT)频谱分析，得到其频域特性以100 Hz为基频，并在基频处噪声声压级达到峰值，再结合变电站各参数，建立声衰减模型，可以较准确的计算出变电站厂界的噪声分布。但由于无法进行干涉计算，因此距离衰减断面5～25 m范围内的中近场噪声分布无法有效预测。Cai Xuan[15]等人通过将110 kV带隔声的室外变压器的每个表面等效于9个点声源，在LMS virtual.lab软件中建立了一个变压器多点等效声模型，对场界噪声的预测小于1.5 dB。但每个变压器需要设置36个点声源，建模与计算效率不高且依然无法解决干涉问题，导致中近场噪声的预测依然存在误差。Wang Rui[16]等人提出了一种基于惠更斯原理的等效源方法。通过构建多点声源模型，模拟实际电容器的声学特性，并重建原始声场。通过物理测试和仿真比较了所提模型与边界元法(BEM)模型的正确性。以上文章都无法对干涉进行计算，成为制约变电站噪声精准预测的一个技术难点。

为解决上述问题，本文使用COMSOL有限元软件，应用声学偏微分方程，从物理本质上对声源建模[17-20]。考虑到之前多使用的点声源、体声源指向性不明显，提出使用双层多线声源的建模方法。该模型能够较好地解决变压器结构不对称和辐射噪声分布不均匀而使得噪声模型难以等效的问题。同时由于是基于物理方程进行建模，因此噪声的干涉性可以得到良好的计算，该模型可为下一步变电站的规划设计与噪声控制提供新思路与方法依据。

1 理 论

声音在传播过程中符合质量守恒定律、绝热压缩定律、牛顿第二定律，可联立上述定律推导出声波波动方程。在空气域中，取边长为dx、dy、dz的平行六面体的媒质中取一微小的体积元，设这一平行六面体媒质的平均密度为ρ，中心点为A(x，y，z)，A沿X轴的速度为Vx，压强为P。又由于在理想的媒质中是不存在切向力的，只有由静压强和质量力所产生的表面作用力。由此，根据声的传播满足牛顿第二定律这一规律，微元体在X方向上的平衡微分方程为

(1)

由质量守恒定律可知，体积元内的质量变化等于单位时间中流入体积元质量与流出体积元质量的差。由此可得到的连续方程如下：

(2)

当声波经过这一体积元时，该体积元内的密度、温度、压强这三个物理量都会发生变化。而这三个物理量所发生的变化其规律可由热力学状态方程描述。在声波的传播过程中一般认为是绝热的，与温度无关，压强仅仅是密度的函数[21]。因为在声波的传播过程中，媒质还来不及与相邻部分发生热交换。因此可以推算出声扰动引起的密度和压强的微小增量之间的关系式[22]：(其中，下角标s表示该过程是绝热过程。由于密度和压强的改变方位一致，所以dP/dρ恒大于0)

(3)

由于声波的各物理量随时间的改变率都很小，因此可以将上述几个方程进行简化，其中ρ=ρ0+ρ′第一二项分别为静态密度和密度增量。对运动方程的简化有：由于在欧拉方程中，质点的速度是时间和坐标的函数，同时，坐标也是时间的函数[23]。其质点的加速度中，一部分是当地的加速度。当地加速度是空间中某一固定点因为时间的改变而导致的速度的改变。略去二级以上的微量便可得到简化后的运动方程[4]：

(4)

连续性方程的化简有：将ρ=ρ0+ρ′代入原方程并略去二级以上的微量便可得到简化后的连续性方程：

(5)

物态方程的化简有：因为压强的微分为声压P，密度的微分为密度增量ρ′。由此得到化简后的物态方程：

(6)

由化简后的运动方程(4)、连续性方程(5)、物态方程(6)即可得到理想媒质中小振幅声波的波动方程：

(7)

从一维推广到三维，此时在直角坐标系中小振幅声波的三维波动方程为

(8)

有限元与边界元都是一种数值计算方法，两者都需要对模型进行网格划分后求解。两者的物理内涵均为基于数学差分法的思想，通过形函数，按不同的划分方式计算不同数量的微元体结点，其平均值即为微元体的值。以划分为二维四边形为例，则任一点的位移都可通过所在单元的结点位移插值表示：

(9)

不同的是，有限元是在全部域空间内划分网格，而边界元只在定义域的边界上划分网格，用满足波动方程的函数去逼近边界条件。所以在处理相同的模型时，边界元的网格数量往往少于有限元，运算量也会相应减少。但是边界元由于计算的线性方程组的系数矩阵是满矩阵，在处理复杂模型时会出现无法收敛的情况。因此本文使用有限元处理复杂模型，增加收敛性，使用边界元处理外部空气域部分，减少网格数量，增加运算效率。再通过对有限元和边界元的耦合，建立了一种兼顾精度与效率的变压器双层多线声源等效模型。

2 模型建立方法

常规的变压器声源模型建立方法为在软件中定义一个点声源或正方体声源代替变压器[24-29]，这样的建立方法指向性较差，无法准确预测噪声的传播。

为了更准确建立声源模型，本文首先对某变电站共有2组特高压变压器进行现场测试，每组分为A、B、C三相，各相之间通过防火墙进行隔离，且每相安装有8台冷却风扇。声压级测量布点在I组变压器三相四周，距离设备立面1 m，高1.5 m。冷却风扇及测点位置详见图1所示。

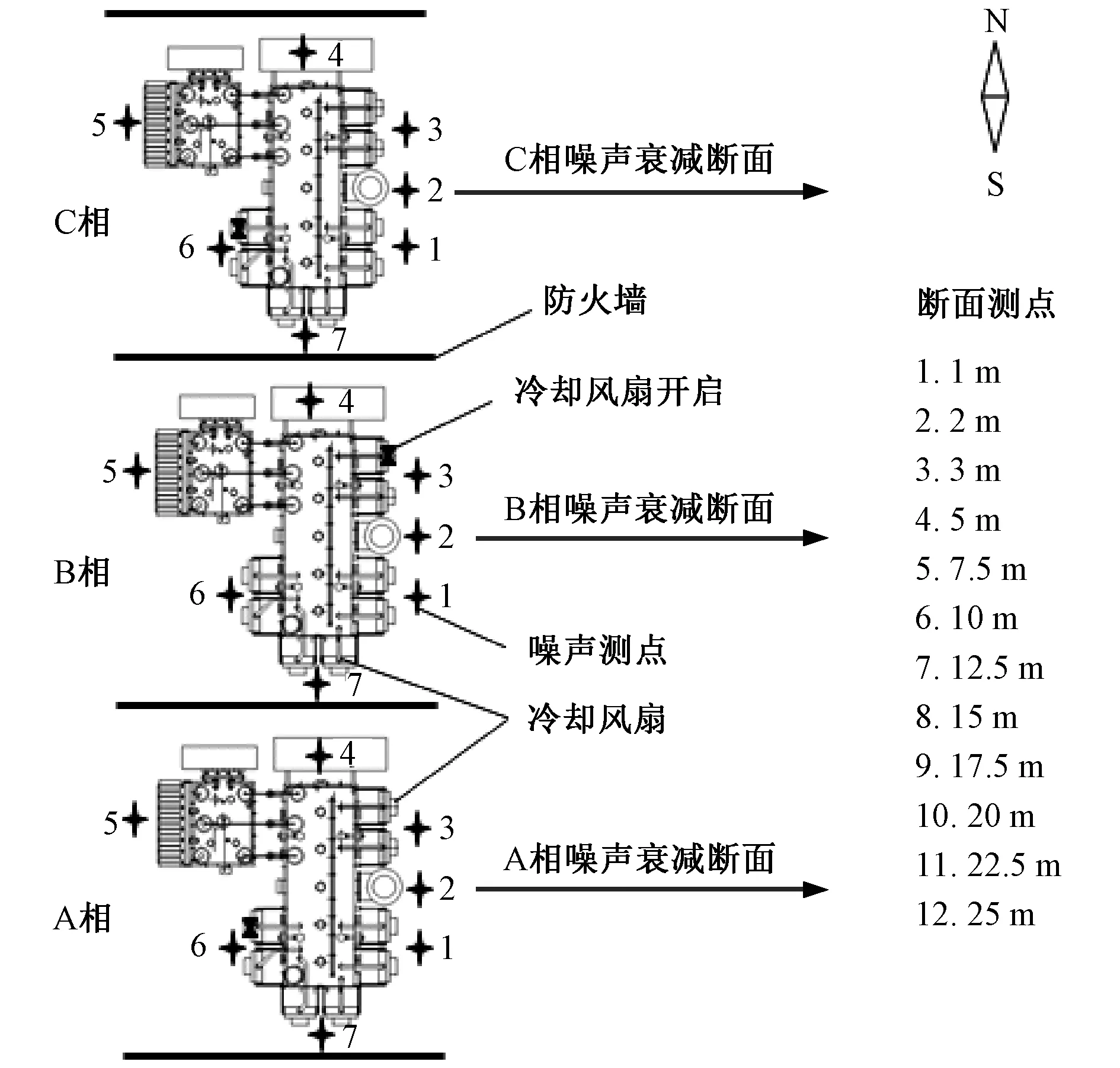
图1 某变电站I组变压器噪声声压级测量布点示意图Fig.1 Schematic diagram of measuring noise sound pressure level of group I transformer in a substation

变电站I组变压器噪声声压级水平如表1所示。

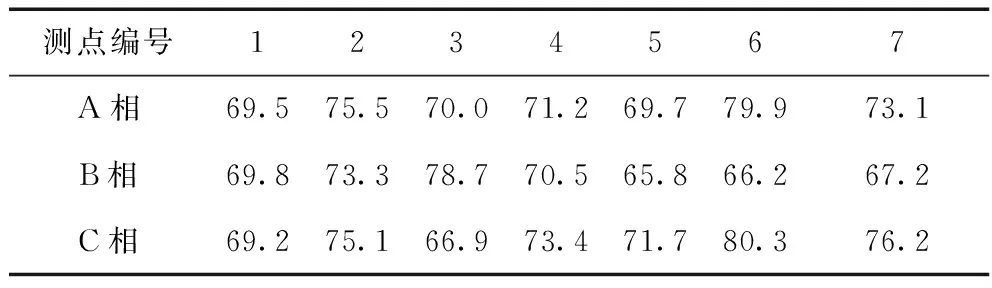
表1 变电站I组变压器噪声等效声级 Tab.1 Equivalent noise level of group I transformer noise in substation dB (A)

测量过程中，变压器正常运行，功率负荷稳定在单组变压器2 000 MW左右，每相变压器仅有一台冷却风扇处于工作状态。由表1可知，距离变压器立面1 m处，噪声最大值为80.3 dB(A)，出现在工作风扇附近；最小值为66.2 dB(A)，远离工作风扇位置。变压器三相的结构和布置相同，但因工作风扇位置不同，相同测点位置的噪声值相差较大。如，A相和C相的工作风扇靠近6号测点，B相工作风扇靠近3号测点，而A相和C相6号测点位置噪声大于B相约14 dB。可知，变压器近场噪声声压级大小受风扇位置影响较大。因此，变压器噪声声压级测量时，需要对变压器四周进行布点，而且需明确工作风扇的位置。

变电站变压器噪声衰减测量布点在I组主变无防火墙的东侧开放边，测点高度1.5 m，从距离变压器发射面1 m处开始布点，前3点的间距为1 m，5 m之后每2.5 m布一点。所得噪声衰减曲线见图2所示。

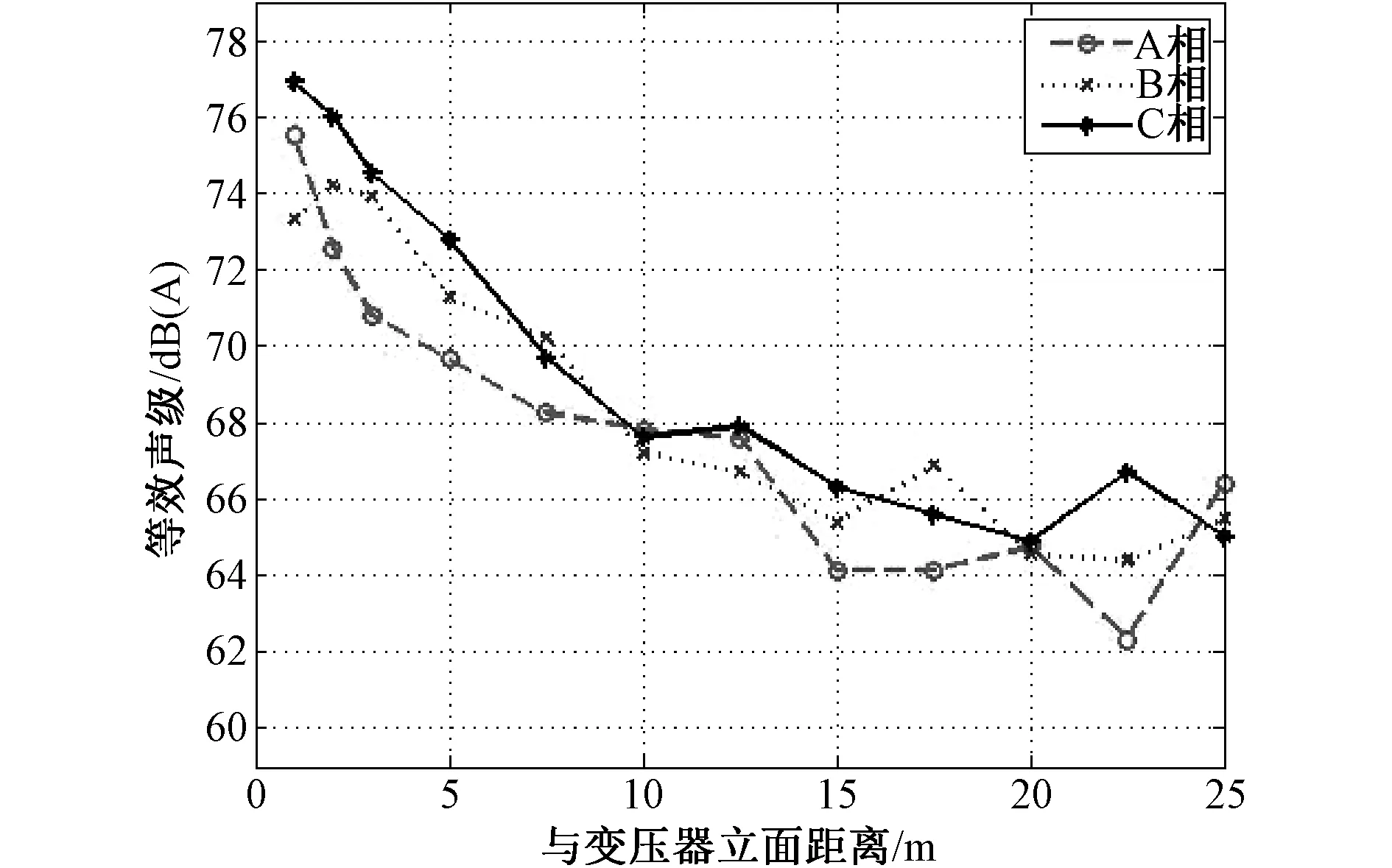
图2 某变电站I组变压器噪声衰减曲线Fig.2 Noise attenuation curve of group I transformer in a substation

由图2可知，变压器各相噪声随距离增加而衰减，衰减趋势基本一致。水平距离10 m内，噪声衰减较快，平均衰减量约1 dB/m；10 m外，噪声衰减较小，外延15 m衰减值约3 dB。另外，距离变压器25 m处，噪声值维持65 dB(A)，且衰减曲线平缓。可知，特高压变压器噪声随距离衰减较小。

使用声级计实测的噪声频谱数据如图3所示，可发现变电站噪声特性明显，峰值频率为100 Hz。

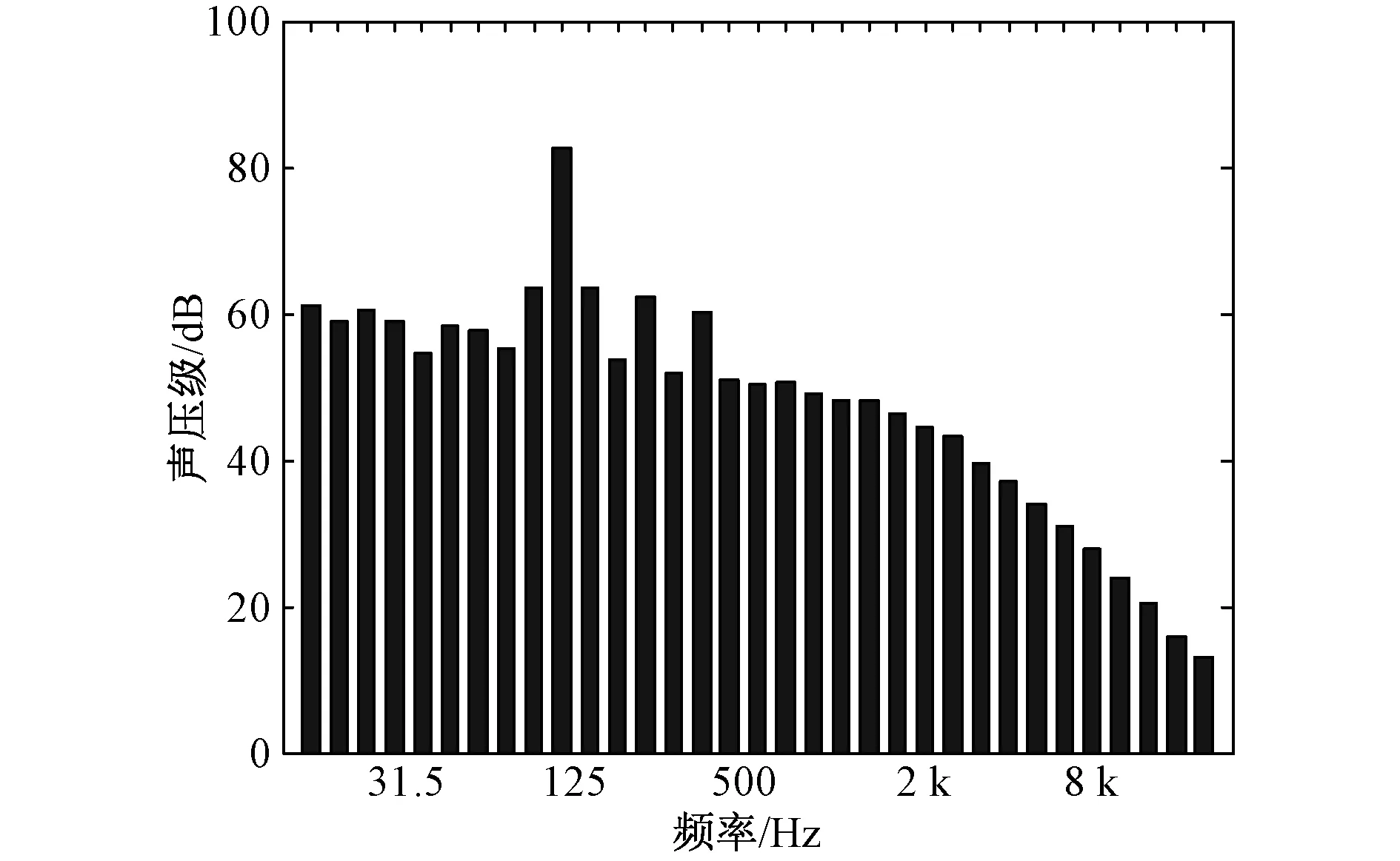
图3 实测变电站噪声频谱图Fig.3 Measured noise spectrum of a substation

根据现场测试情况，本文提出一种双层多线声源法建立变压器声源等效模型。按照现场测试的衰减最大距离，定义了以变压器外边界为起点，分别向x、-x、y、-y和z五个方向延伸25 m的范围为边界元大小。根据《ISO 9613-2∶1996声学-户外传播时声音的衰减-第2部分：一般计算方法》，此时地面可设置为刚性地面。其模型图及边界元范围如图4所示。

图4 模型图及边界元范围Fig.4 Model diagram and boundary element range

仿照变压器的真实结构，同时又要方便定义声源。变压器模型的结构由6块长3 m，宽2.5 m，高1.5 m的长方体，3块长2.5 m，宽2.5 m，高1.5 m的长方体，3块长3 m，宽2 m，高1.5 m的长方体和3块长3 m，宽1 m，高1.5 m的长方体组成，共计15块长方体。双层多线声源分别取模型高度1/3处及2/3处分段环绕一周设置，频率设置为变电站的主频100 Hz。将实测的A、B、C三相的声压级计算出算数平均值，之后再根据(10)、(11)式将实测声压级换算成声功率定义线声源，换算后的等效线声源声功率见表2，其中线声源编号与测点编号相对应。其模型及双层多线声源设置如图5所示。

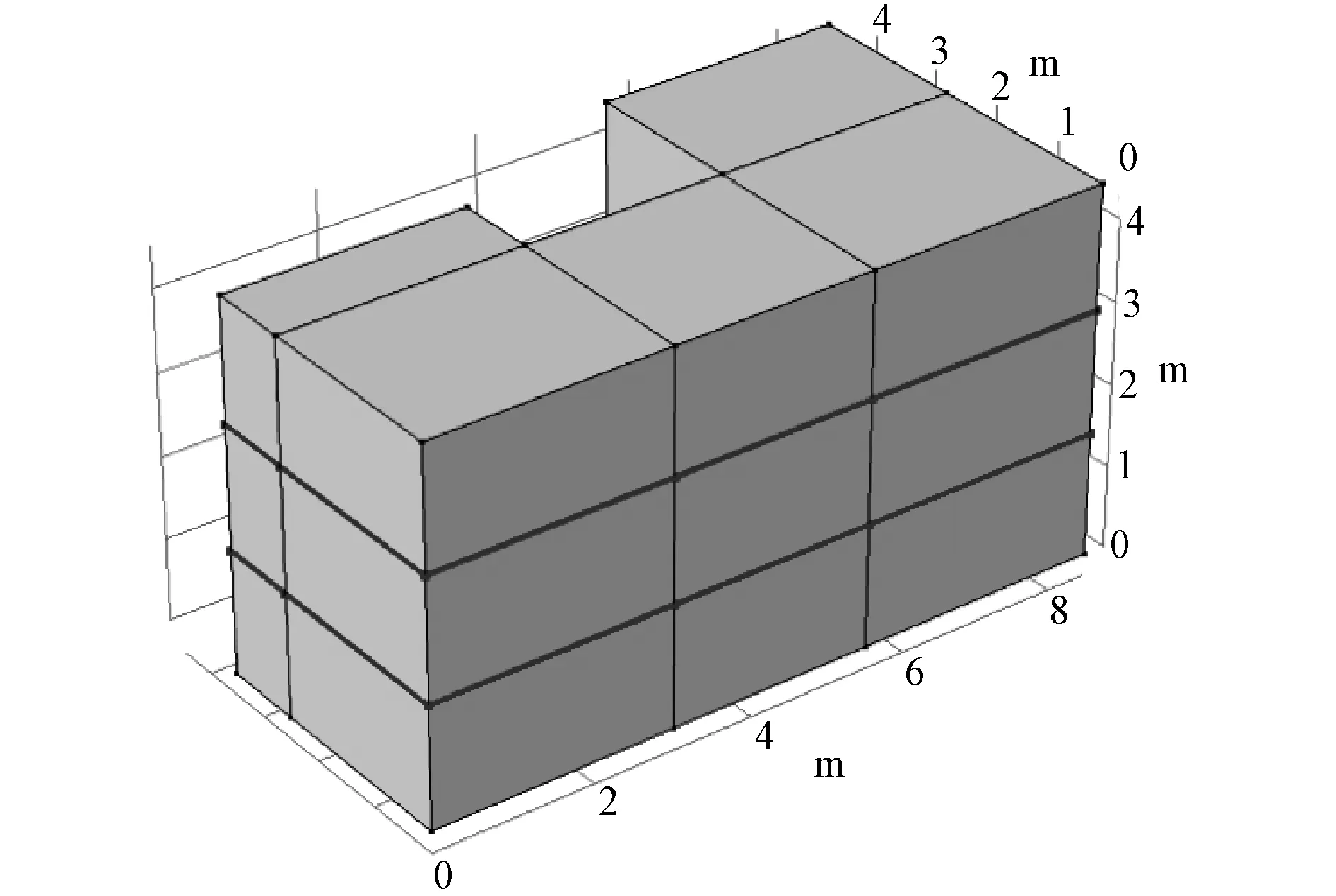
图5 模型及双层多线声源Fig.5 Model and double-layer multi-line sound source

表2 等效线声源声功率(均方根)Tab.2 Sound power of equivalent line sound source (root mean square) (W)

LP=LW-10lg(4πr2)

(10)

LW=10lg(W/W0)

(11)

式中：LP为声压级；LW为声功率级；r为声压测点距声源距离，本文为4 m。W为声功率；W0为基准声功率，大小为10-12W。

为了跟实测数据比对，从x=3 m，y=-1 m，z=1.5 m处开始，在y=-1 m、-2 m和-3 m分别布点。之后从y=5 m开始，每隔2.5 m布一点直到y=-25 m处停止，共计布点12处。

3 结果与讨论

通过有限元-边界元耦合仿真，得到变压器声压级双切面云图和声压双切面云图如图6、图7所示。通过声压级双切面云图可以明显观察到变电站噪声的传播具有指向性，在y轴的正负方向及x轴负方向皆有明显花瓣型声密集区，如图中黄色部分。在密集区俩侧则为声疏区，如图中蓝色部分。通过声压云图可以明显看到，声波的干涉效应在有限元-边界元耦合的方法下得到很好的体现。证明本文所用方法可以解决SoundPLAN等商业噪声预测软件无法解决的干涉现象。

图6 变压器声压级双切面云图Fig.6 Double cut cloud of transformer sound pressure level

图7 变压器声压双切面云图Fig.7 Double cut cloud of transformer sound pressure

根据在COMSOL中的布点，做出仿真噪声衰减曲线与实测声压级平均衰减对比图，以及仿真与实测噪声差值如图8、9所示。

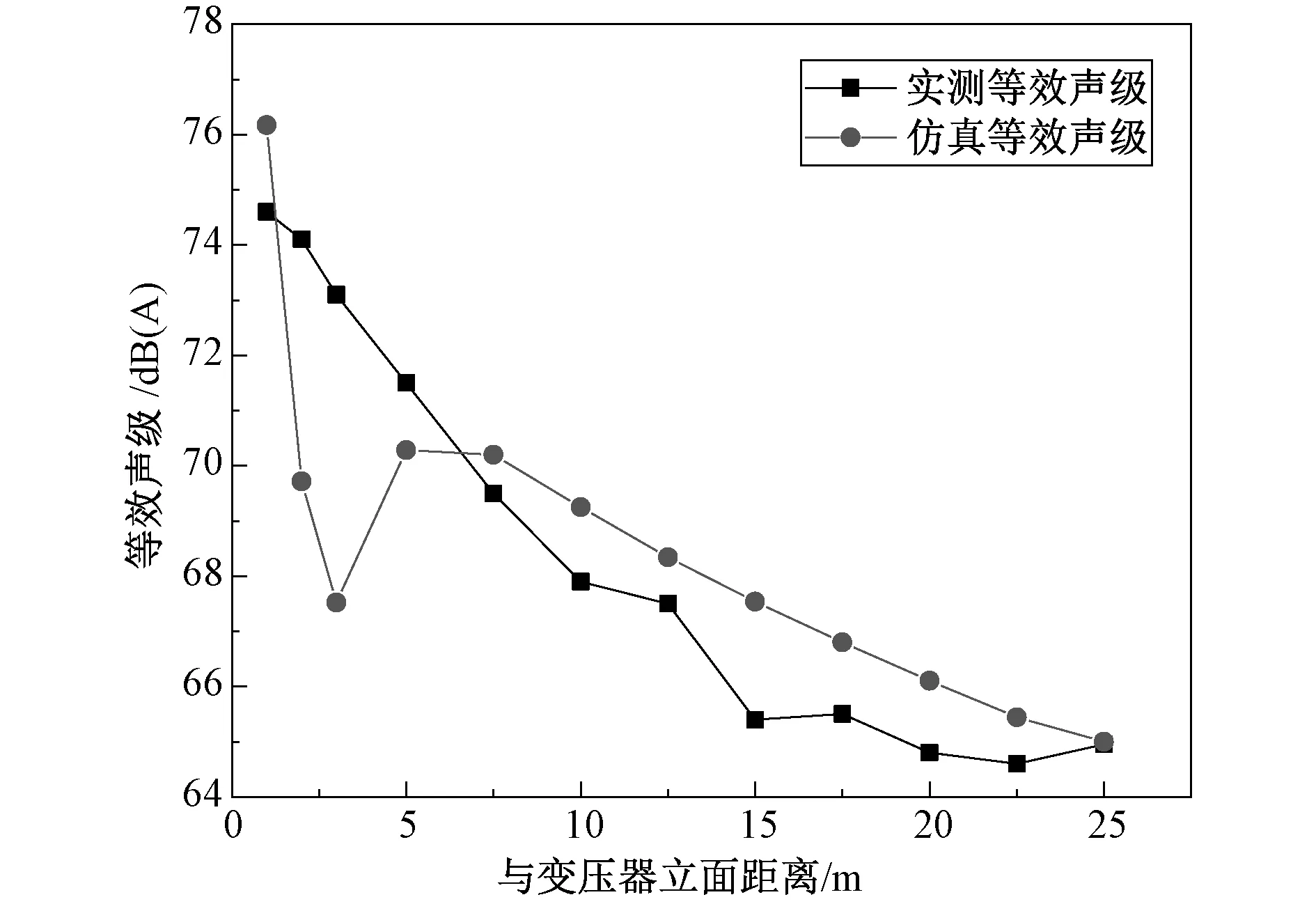
图8 仿真与实测噪声衰减对比图Fig.8 Comparison of simulated and measured noise attenuation

通过与实测数据比对，可发现在距离变压器立面距离5 m之后仿真数据与实测平均数据的误差基本控制在3 dB以内。在起点处，仿真数据相比实测数据可见明显下降，呈现出一个波谷。分析原因为仿真声源为100 Hz单频声，在距离变压器立面距离3 m之内，线声源之间发生了明显的干涉现象，导致声压级在某些坐标的下降。而在5 m之后，其衰减相比变电站复杂频谱的噪声更加平缓，因为真实的变压器噪声不仅有本体的低频噪声，还有风机的中高频噪声，且还存在背景声场的影响。因此，仿真数据和真实测量值出现一定差异。同时，由于高频声相对低频声随距离的衰减更大，这就导致随着距离的增加，仿真数据和实测数据的差值逐渐缩小，在25 m处的差值仅为0.05 dB。

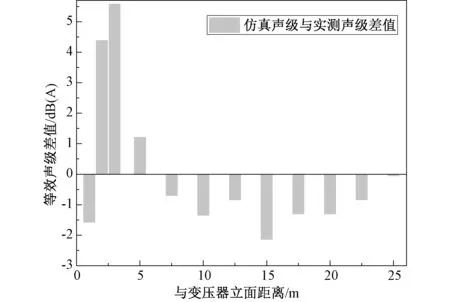
图9 仿真与实测噪声差值Fig.9 Difference between simulated and measured noise

4 结 论

通过对变压器噪声实测，可以发现噪声主要集中在100 Hz及其谐频处。由于频率较低，因此随着距离变化的衰减较小。通过有限元-边界元耦合理论，建立了变压器双层多线声源等效声源模型。通过对模型进行数值仿真，可以明显观察到变电站噪声的传播的指向性，在y轴的正负方向及x轴负方向皆有明显花瓣型声密集区。同时，声波的干涉效应在有限元-边界元耦合的方法下得到很好的体现。证明本文所用方法可以解决SoundPLAN等商业噪声预测软件无法解决的干涉现象。通过与实测数据比对，可发现在距离变压器立面距离5 m之外，仿真噪声衰减数据与实测噪声衰减平均数据的误差基本控制在3 dB以内，较精准的预测了变压器噪声传播与衰减，验证了本文所建模型的有效性及高精度性，可为今后特高压输变电工程的精细化设计提供理论依据和方法指导。