形态小波与模糊熵在齿轮故障分类中应用
2020-10-12张志刚姚练红
丁 伟,张志刚,姚练红,黄 捷
(1.重庆电子工程职业学院 智能制造与汽车学院, 重庆 401331; 2.重庆理工大学 汽车零部件先进制造技术教育部重点实验室, 重庆 400054;3.重庆青山工业有限责任公司 技术中心, 重庆 402761)
变速器作为装甲车辆传动系统关键总成之一,其齿轮故障往往会引起变速器整箱失效,从而导致整个传动系统无法正常工作。然而,由于变速器结构复杂,激励源多,变速器齿轮故障信息常常被淹没于强噪声信号。因此,研究强噪声环境下变速器齿轮故障识别与分类方法已经成为变速器故障诊断的研究重点。研究表明,发生故障的变速器齿轮振动信号特征具有典型的非平稳性和非线性,所以,研究变速器齿轮故障信号的有效提取与分类方法尤为关键[1-3]。Huang等[4]在齿轮箱故障诊断中提取了频谱归一化幅值。Crabtree等[5]从多特征参数角度对齿轮箱早期故障进行了检测。Zimroz等[6]提取了齿轮箱的瞬时转速。唐新安等[7]借助时域统计指标实现齿轮箱故障的初步诊断。胡茑庆等[8]提出基于希尔伯特-黄谱的啮频邻域内能量特征来检测行星齿轮箱太阳轮断齿故障。模糊熵作为一种新型非线性方法,用来对采样序列的维数发生变化时衡量其产生新模式概率大小的方法,所具有的物理意义与样本熵相似。而且由于模糊熵采用指数函数代替单位阶跃函数[9],指数函数所具有的连续性让采样序列计算得到的模糊熵值呈现出跟随参数变化能连续的平滑变化的趋势[10-12]。但是在进行特征参数提取前,由于原始采样信号会受到各种噪声的干扰,因此选择合适的降噪方法对原始信号进行降噪预处理,对后续提取反映故障的特征参数将起到积极的作用。
形态小波作为一类非线性小波,既保持了数学形态学的形态特性,又继承了传统小波的多分辨率特点,具有较好的抗噪性能和良好的细节保留特性。Goutsias等[13-14]采用数学形态算子代替传统小波的线性算子,构造了形态小波(morphological wavelet)。文献[15]采用形态小波对转子信号进行了降噪处理取得了较好的效果。因此,本文在深入研究形态小波和模糊熵的基础上,提出基于形态小波和模糊熵的齿轮故障分类方法,对齿轮不同工况下的振动信号首先进行形态小波降噪预处理,然后提取模糊熵,同时为了便于比较,对原始信号提取模糊熵,结果表明模糊熵有较好故障分类能力。
1 形态小波的基本原理
形态小波是在数学形态学的基础上,采用数学形态学中的算子对传统线性小波的非线性扩展。数学形态学及其相关算子的内容可以参见文献[15],在此不再叙述。下面基于对偶小波分解和非对偶小波分解[13-14]基本概念定义形态小波。
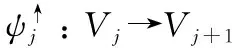

图1 对偶小波分解示意图
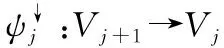
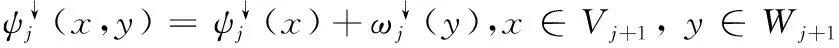
(1)
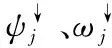

图2 非对偶小波分解示意图
由于Haar小波结构简单和形态特点[14],所以采用非对偶小波分解方案构造形态Haar小波如下:
(2)
(3)
(4)
(5)
式中: “∨”—形态膨胀算子(极大值);“∧”—形态腐蚀算子(极小值)。
当式(2)中信号分析算子采用腐蚀运算时,则式(2)~(5)构造的形态Haar小波为具有腐蚀算子的形态Haar小波;反之,用形态膨胀算子代替式(2)~(5)中形态腐蚀算子,则可构造具有膨胀算子的形态Haar小波。本文研究中采用具有膨胀算子的形态Haar小波对变速器齿轮故障信号进行降噪预处理。
2 模糊熵的定义
假设齿轮故障信号的原始时间序列为:[x(n)]=x(1),x(2),…,x(N),总共得到N个采样点,则齿轮故障信号的采样序列模糊熵[10-12]可按照下列步骤得到:
1) 将齿轮故障信号的采样时间序列按照采样序号组成一组m维的向量。
2) 定义不同向量Xm(i)与Xm(j)之间距离d[Xm(i),Xm(j)](i≠j)为两个向量对应元素中计算所得最大差值。
4) 定义函数
(6)
5) 以此类推,将维数增加到m+1,重复步骤(1)~(4),可得
(7)
6) 齿轮故障信号的时间序列模糊熵为
(8)
当N为有限数时,式(8)可表达为
FuzzyEn(m,r,N)=InΦm(r)-InΦm+1(r)
(9)
式中:m为模式维数;r为相似容限;N为数据长度。
3 形态小波与模糊熵的齿轮故障分类原理
当变速器齿轮存在裂纹、断齿等故障时将产生冲击特征,由于冲击成分存在,导致变速器齿轮振动信号时域上表现出一定形态特征。运用形态Haar小波对齿轮振动信号进行降噪预处理,进一步计算降噪处理后的齿轮振动信号模糊熵,通过对比变速器齿轮不同类型故障信号的模糊熵差异进行齿轮故障识别与分类。
图3给出了形态小波与模糊熵齿轮故障分类的计算流程,齿轮故障分类的具体步骤如下:
1) 采用形态Haar小波对齿轮故障信号分解,可得第1层、第2层、…、第J层的近似信号和细节信号;
2) 将第1层、第2层、…、第J层的细节信号进行软阈值降噪处理;
3) 运用各层降噪处理后的小波细节系数进行重构故障信号;
4) 计算重构故障信号的模糊熵,依据齿轮故障信号模糊熵值对齿轮故障状态有效分类。
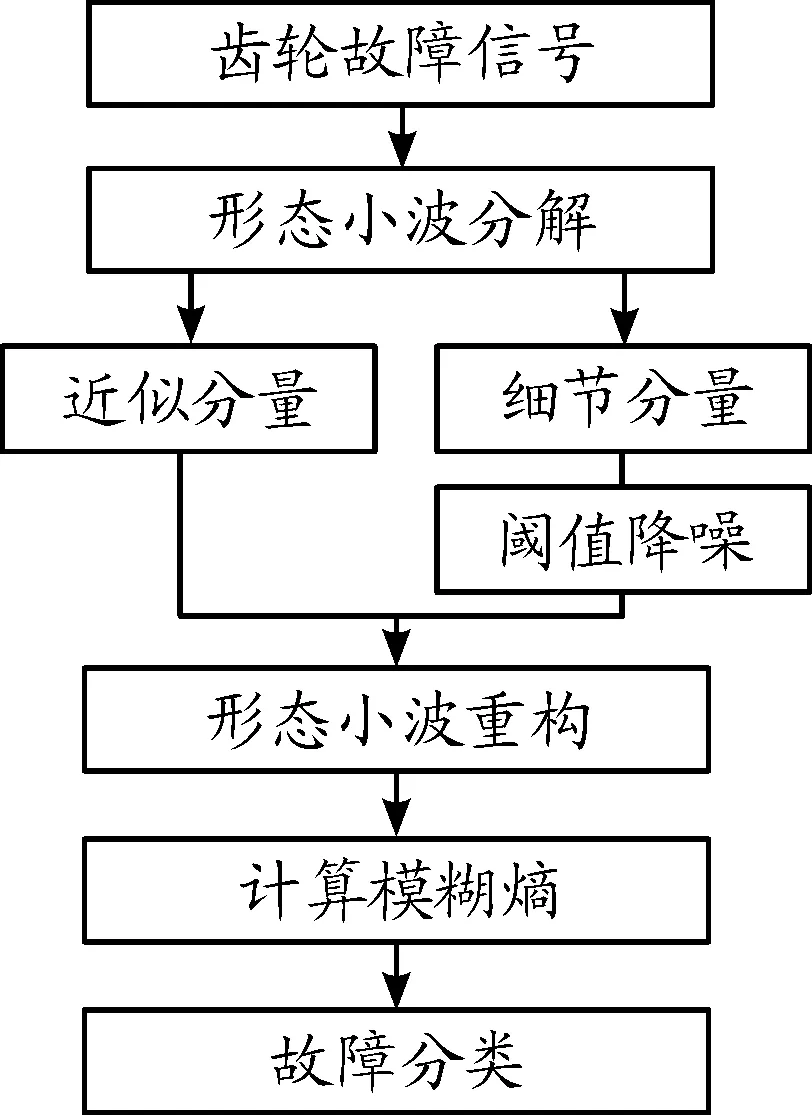
图3 齿轮故障分类流程框图
4 实例分析
为了验证模糊熵在变速器齿轮故障分类中优越性,基于齿轮故障试验台,分别测得齿轮正常、齿面轻度磨损、齿面中度磨损和断齿等四种常见工况的振动信号。被试齿轮转频为fr=23.6 Hz,啮合频率为fz=686 Hz,振动信号的采样频率为16 384 Hz。通过更换有缺陷的齿轮,可模拟各类齿轮故障。首先引入形态Haar小波对原始采样信号进行降噪预处理,然后对降噪后的各种工况振动信号计算其模糊熵。限于篇幅,以齿轮正常信号为例,图4给出了齿轮正常信号的形态Haar小波降噪前后时域波形及其频谱。将各工况齿轮振动信号进行形态Haar小波分解,选取分解层为3层,将分解得到的各层细节信号经软阈值降噪处理,再进行信号重构得降噪后的各工况齿轮振动信号。
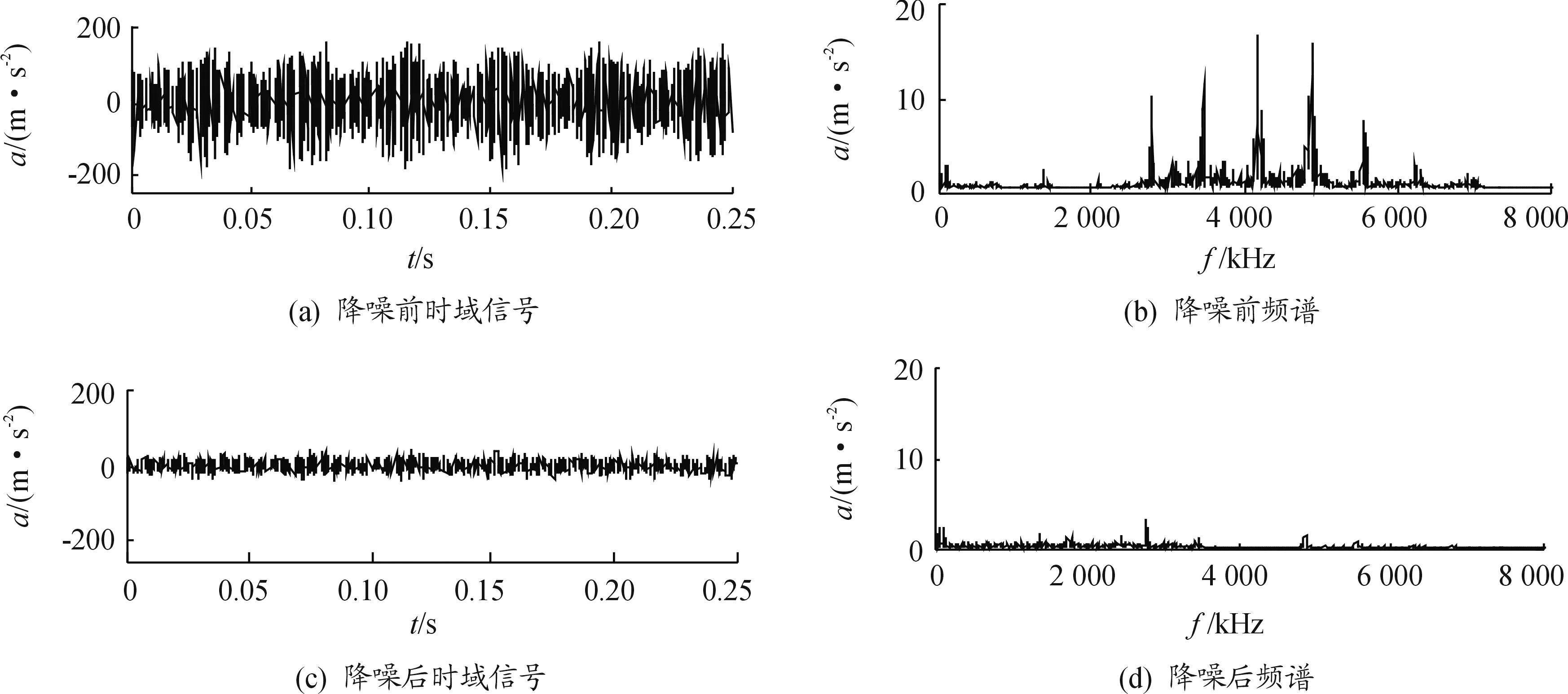
图4 齿轮正常信号形态Haar小波降噪前后时域波形及频谱曲线
对比齿轮正常信号降噪前后频谱,可知齿轮正常信号经过形态Haar小波进行降噪处理后,原信号中所含高频噪声得到了较好抑制,这对于齿轮振动信号进行后续特征参数计算具有重要意义。
文中选取模糊熵为故障信号特征参数,计算齿轮4种不同工况信号的模糊熵,文中选取m=2,r=0.2 Std。限于篇幅,图5给出了每种工况10组采样数据的模糊熵。“•”代表齿轮正常工况信号的模糊熵;“○”代表齿面轻度磨损工况信号的模糊熵;“+”代表齿面中度磨损工况信号的模糊熵;“x”代表齿轮断齿工况信号的模糊熵(以下皆同)。
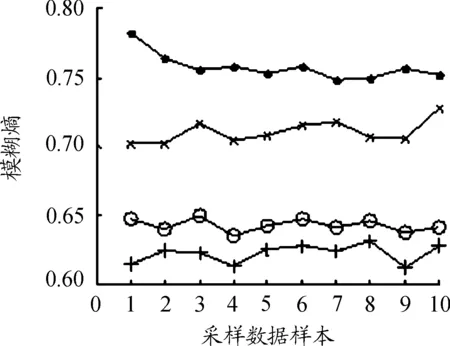
图5 齿轮4种工况的模糊熵曲线
由图5可知,齿轮在不同的故障状态下提取得到的模糊熵呈现出明显的区别,而且模糊熵值分布比较平缓,所表现出的不同工况的分类效果较好。从图中还可以看出,齿轮正常工况信号的模糊熵值最大,说明其采样数据的随机性最大。而齿面轻度磨损在振动信号监测中最不易观察到,因此其所表现出的故障特征最不明显,而采用模糊熵作为特征参数,齿面中度磨损与轻度磨损在图中得到了很好的区分。基于以上良好的分类能力,模糊熵可以用来区分齿轮不同故障模式下的振动信号。
为便于对比,图6给出上述四工况齿轮原始振动信号的模糊熵。对比图5、图6可知,除了正常信号的模糊熵值能明显区分外,其余3种工况计算得到的模糊熵存在严重交叉,无法有效区别齿轮的故障类别。

图6 齿轮4种工况数据未降噪前的模糊熵
文献[16]也类似采用本文所使用的齿轮故障数据,该文献采用顺序形态滤波进行齿轮故障信号降噪处理,通过提取降噪信号的奇异熵进行齿轮故障分类识别。通过对比该文献中降噪处理后的不同工况信号奇异熵的分布情况,和本文中采用形态小波降噪处理后的信号模糊熵分布情况可知,该文献降噪后提取的不同工况的奇异熵值差异小,虽然也能对信号进行分类,但效果不如本文降噪后提取的模糊熵效果明显,这也显示了本文所提出方法的有效性。
5 结论
1) 由于原始故障信号噪声干扰,直接用于计算模糊熵值存在交叉,无法有效识别故障类别。采用形态小波降噪后,原始信号中噪声信息得到了较好抑制,所计算出的模糊熵能有效用于区分不同故障类别。
2) 基于齿轮故障试验台实测齿轮不同工况信号进行了模糊熵计算和故障分类,为装甲车辆变速器齿轮故障状态识别与分类提供了一种新途径。
