静载拉伸过程的磁声发射特性仿真与实验研究

曾文钧,李志农,沈功田,闻庆松,沈永娜

(1.南昌航空大学 无损检测技术教育部重点实验室, 南昌 330063；2.中国特种设备检测研究院， 北京 100029)

磁声发射检测技术是在声发射技术和磁巴克豪森效应的基础上发展起来的一种磁性无损检测技术[1]。它指的是铁磁性材料在磁化的过程中，由于磁畴壁的不可逆运动，在产生巴克豪森跳跃的同时释放一种弹性应力波，同时伴随着磁致伸缩效应而产生的一种声发射现象。材料的磁致伸缩应变而产生的弹性波[2]。相较于磁巴克豪森技术只能检测构件表面或近表面(<1 mm)应力状况，磁声发射技术不仅能够弥补其检测深度上的不足(最大可达10 mm)[3]，而且具有灵敏度高、测量数据更稳定，可以对整个结构进行评价等优点。

磁声发射现象最早由Lord[4]于1974年发现的，观察到镍在被磁化的时候会产生大量的声发射信号，而且该信号仅在对应于磁滞回线陡峭处的磁场范围内产生。该声发射信号主要是由于材料微观层面上的体积的不连续变化引起的，并且可以通过压电传感器检测到。目前，对于用磁声发射方法来表征铁磁性材料应力变形程度和微观组织变化已经有了较多的相关研究。徐约黄等[5-6]以45钢、硅钢片以及纯铁试样为材料，研究了在不同拉应力下的磁声发射信号，发现这些材料的磁声发射信号都随试样受拉应力的增大而单调下降。穆向荣[7]、Augustyniak[8-9]、Piorowski[10]等研究了塑性变形对磁声发射的影响，发现磁声发射信号随变形量的增加而呈现出规律性的变化。Sullivan等[11]用磁声发射法来表征铁素体不锈钢(AISI430)的微观结构变化与应力变形状态之间的关系，提出了一种基于磁声发射绝对能量波形的定量检测方法。经MBN和XRD法验证结果表明在塑性变形区随位错密度增加和位错胞的形成，磁声发射的绝对能量成明显下降趋势，为铁磁性构件的疲劳损伤评估奠定了基础。本文以Q235钢为研究对象，通过有限元的方法，分析了不同拉伸载荷构件的应力分布，利用基于能量守恒的励磁耦合模型对试件磁场进行了仿真研究，并通过实验对静载拉伸下的磁声发射特性进行了深入的研究。

1 励磁耦合模型的建立

根据铁磁学的相关研究[12-15]可知,当铁磁性试件受到外加应力大小为σ的载荷时候，其内部产生的应力能为：

2λ[111]cosθ1cosθ2+cosθ3cosθ2+cosθ1cosθ3]

(1)

式中，λ[100]、λ[111]为材料的各向磁致伸缩系数；θ1、θ2、θ3分别为单晶轴与不同磁化方向的夹角。假设材料的磁致伸缩为各向同性，则有λ[100]=λ[111]=λσ。于是式(1)可以简化为：

(2)

式中，θ为等效应力与磁化方向的夹角。当进行单轴拉伸时，应力方向与磁化方向平行，此时，cosθ=1，于是式(2)可以化简为：

(3)

根据电磁场理论可知[16]，

(4)

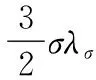
(5)

将式(4)和式(5)相结合并化简可以得到式(6)：

(6)

式中，Bm为饱和磁感应强度;λm为饱和磁致伸缩系数，为不受外力时材料的初始相对磁导率，三者的取值均与材料本身有关。μσ为应力σ作用下材料的相对磁导率。通过式(6)可知构件在不同的应力下，可得到相对应的磁导率。

2 仿真与讨论

仿真模拟的对象是长280 mm，宽60 mm，厚8 mm的Q235钢板。利用多物理场仿真软件COMSOL建立C芯励磁的三维实体模型，并定义好试件的弹性模量、泊松比、屈服强度等材料参数，各材料参数值如表1所示。三维模型采用四面体单元网格划分，最终的网格划分如图1所示。

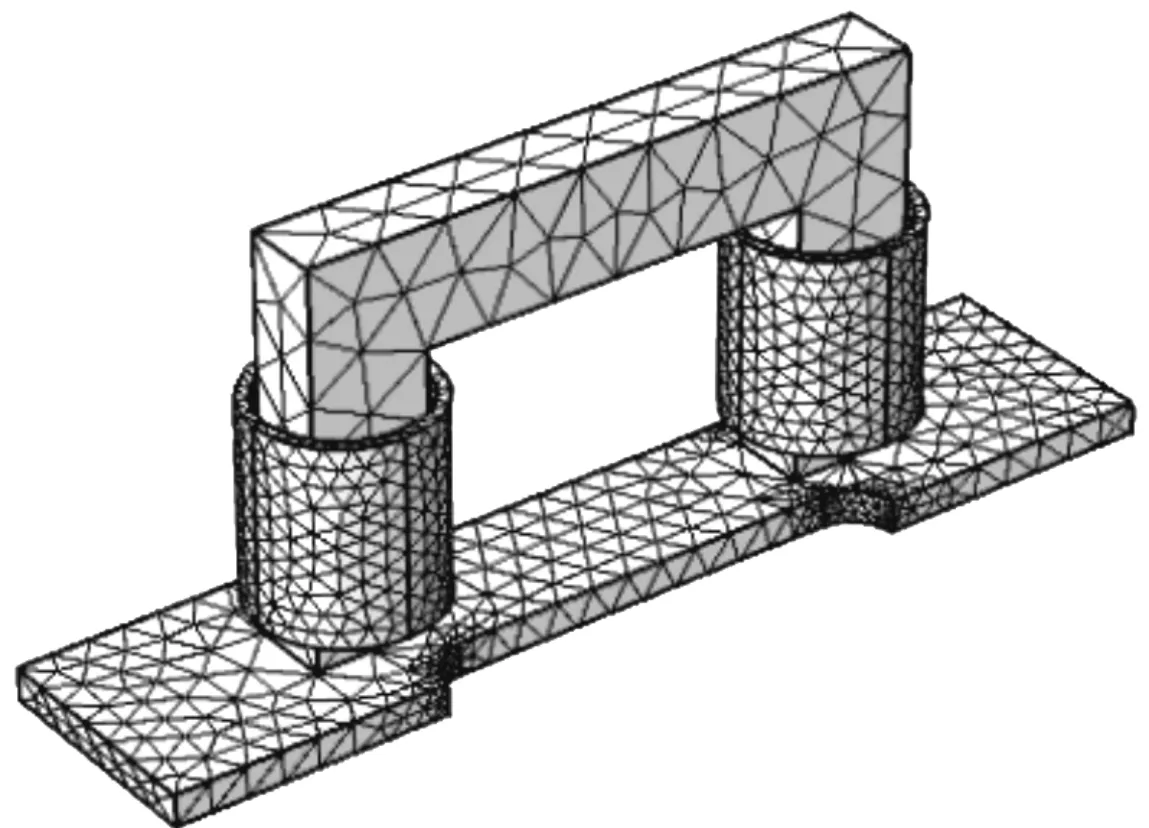
图1 网格划分

表1 Q235 钢主要参数

为了提高计算精度和收敛性，将试件和线圈部分采用局部精细网格划分，这样可以有效地提高网格划分的可靠性。首先做固体力学仿真，将试件沿长度方向的一端进行固定约束，另一端施加水平拉应力。采用稳态研究，可以计算并得到不同的拉伸载荷下的试件的应力分布云图。

在弹性阶段范围内，本文预设了10组应力值，代入式(6)计算可以得到这10组应力值所对应的磁导率的数值，具体数值见表2。如图2(a)到图2(d)所示，分别是40 MPa、100 MPa、160 MPa以及220 MPa拉伸应力下的应力分布云图。从图中可以很明显地看出，中间区域由于受力面积小，故而受到的应力值大于两端的应力值，且应力主要集中在试件的4个圆角处。随着载荷从40 MPa逐渐增大到220 MPa，试件所承受的应力也逐渐增大。当拉伸应力达到220 MPa。

表2 弹性阶段不同应力所对应的磁导率

图2 不同载荷下的应力分布云图

可以从图2(d)中看出，圆角处的最大应力值甚至接近500 MPa，远超过了Q235材料的屈服强度，此时将产生局部塑性变形。图3是从一个圆角端点到另一个圆角端点的有效塑性应变的定义路径。各点的有效塑性应变的值如图4所示，当拉应力大于120 MPa的时候，可以看到有效塑性应变开始累加，并且随着拉应力的增大，累积的有效塑性应变也会越大。当累积的塑性应变达到一定的值的时候，那么试件就可能会发生断裂。因此，试件的中间部分可能会先于别处发生断裂。

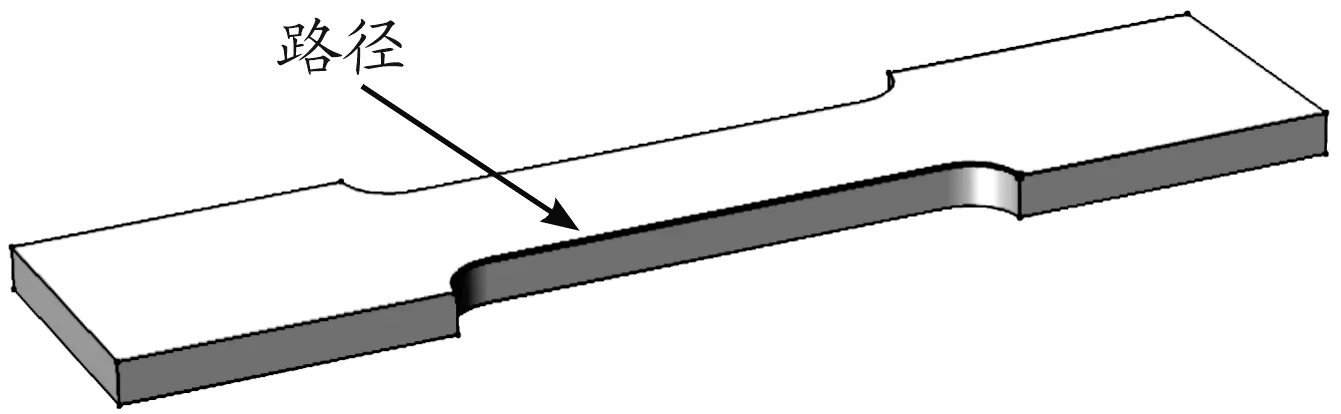
图3 有效塑性应变的定义路径

1.应力为220 MPa; 2.应力为120 MPa; 3.应力为30 MPa

接着，对试件做静磁学模拟。设置空气和试件磁学材料属性，其中空气单元的相对磁导率设置为1，Q235的初始相对磁导率μσ、饱和磁感应强度Bm、磁饱和磁滞伸缩系数λm和矫顽力He来自前期磁化试验测得[18]。根据建立的基于能量守恒的应力-磁导率模型对试件磁导率进行网格单元的循环赋值，并给初级线圈通上峰值为4 V，频率为50 Hz的正弦交流电，模拟忽略C芯和试样之间的任何空间的漏磁效应。图5表示了在没有外部拉伸应力时，在不同时段的试件上的感应电场的方向。其中，图5(a)表示了时间为40 ms时线圈在试件上产生的感应电场方向，是逆时针方向，图5(b)表示了时间为80 ms时线圈在试件上产生的感应电场方向，呈现出顺时针方向。

图5 不同时段的试件上的感应电场的方向和大小

从图6(a)到图6(b)可以看出，时间从42.5 ms到80 ms，磁场的感应电场方向发生了偏转，这和图5相对应。图7是不同时刻试件上下表面两个点的感应电流密度的大小，可以看到越靠近试件表面处的感应电流越大。

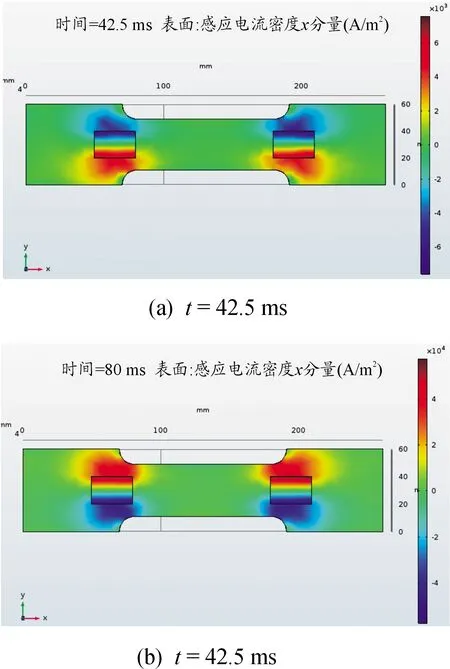
图6 不同时刻的各点的感应电流密度x分量

1.上表面; 2.下表面

根据应力-磁导率的模型，给试件循环附加上由于应力作用而变化的磁导率。通过软件计算得到在试件上由于磁导率的改变而耗散的功率。如图8所示，随着应力的增大，试件上的耗散的功率不断增大，根据能量守恒，试件在磁化的过程中，损耗的能量越大，那么释放的能量变少，磁声发射能量也就越低。

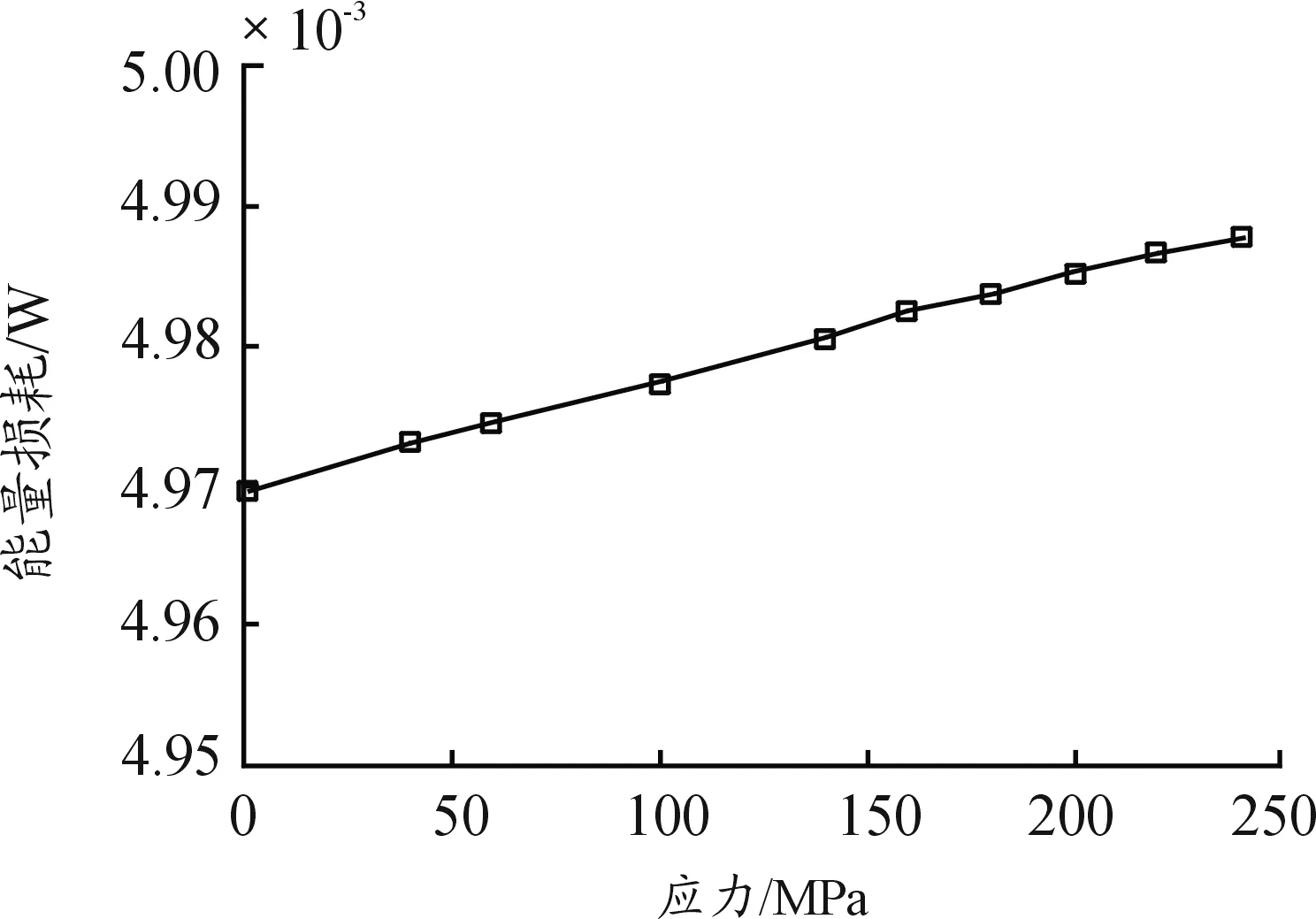
图8 应力-能量损耗曲线

3 实验

实验选取厚度为8 mm的Q235钢作为实验材料，静载拉伸实验采用日本津岛电子万能材料试验机AG-25TA，采用夹头位移速率恒定的加载方式，加载速率为0.3 mm/min。在试样夹持之后未加载应力之前对试样进行MAE测试。分别在励磁频率为10 Hz和50 Hz，输出正弦电压幅值为1～3 V条件下，磁场方向平行于轴向时，采集MAE数据。为了取得多组数据样本。对试样在弹性应力范围(0～240 MPa)进行3次加载、卸载，加载过程中每个20 MPa保载，并进行MAE数据采集。对试件在各应力状态下进行MAE检测时，采用正弦波电压对试样进行励磁并采集信号。

采用正弦波励磁时，MAE信号特征参数随弹性应力的变化如图9～图12。由图可知，随着应力的增大，磁声发射信号的均方根电压和包络面积单调下降。当励磁频率相同时，随着励磁电压的增大，尽管在同一应力水平下，磁声发射信号的绝对值不断增大，但是磁声发射的均方根电压-应力的关系曲线却几乎平行，说明磁声发射信号的变化速率不受励磁电压的影响。当应力由20 MPa增大至240 MPa，励磁频率为10 Hz时，磁声发射信号均方根电压的变化率为36%左右，励磁频率为50 Hz时，则为40%左右。因此当励磁频率为50 Hz时，磁声发射信号均方根电压对应的更为敏感。磁声发射信号包络面积的变化规律则与均方根电压相似。

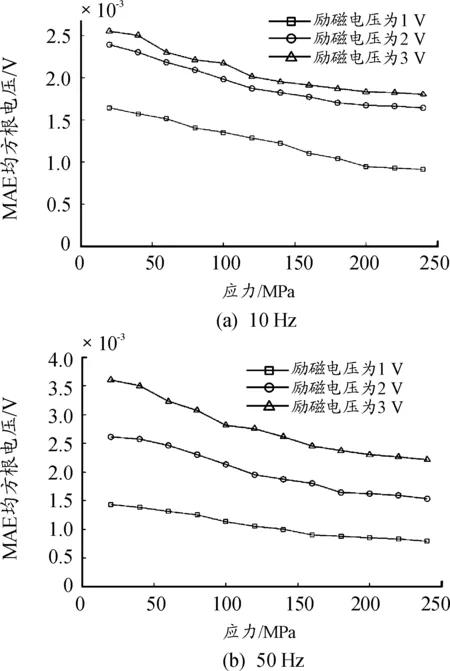
图9 不同励磁频率下，MAE均方根电压-应力曲线

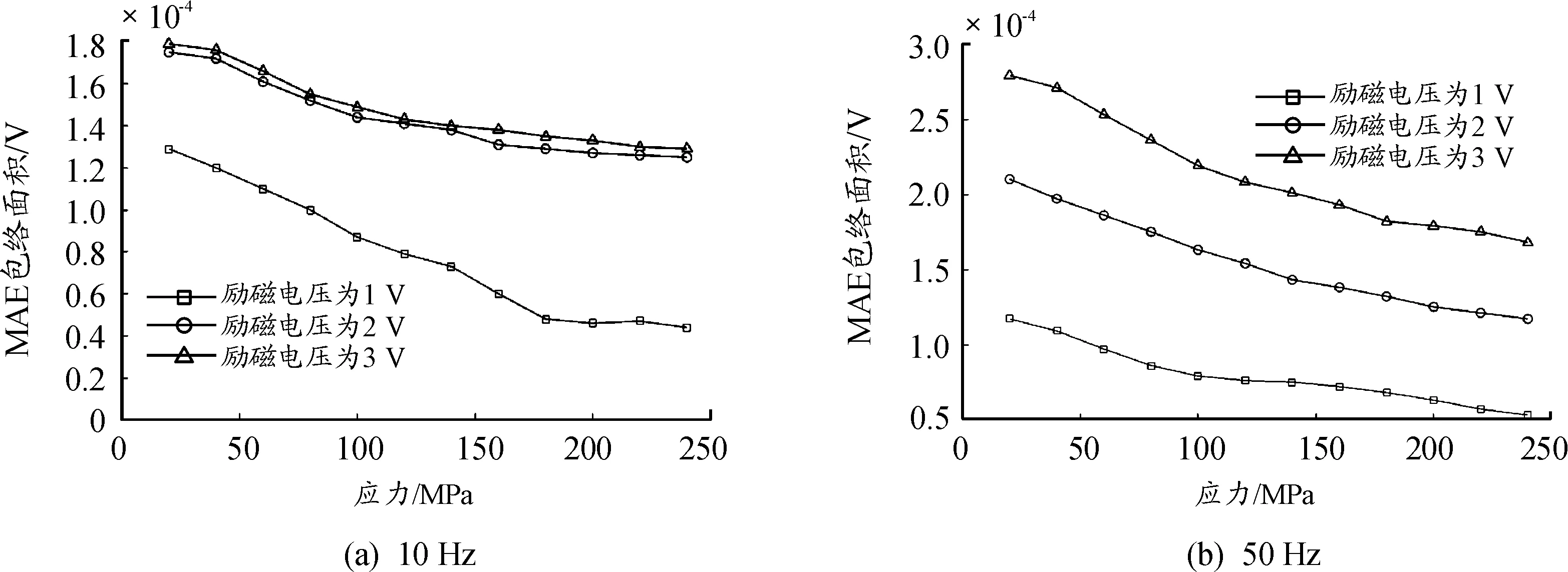
图10 不同励磁频率下，MAE包络面积-应力曲线

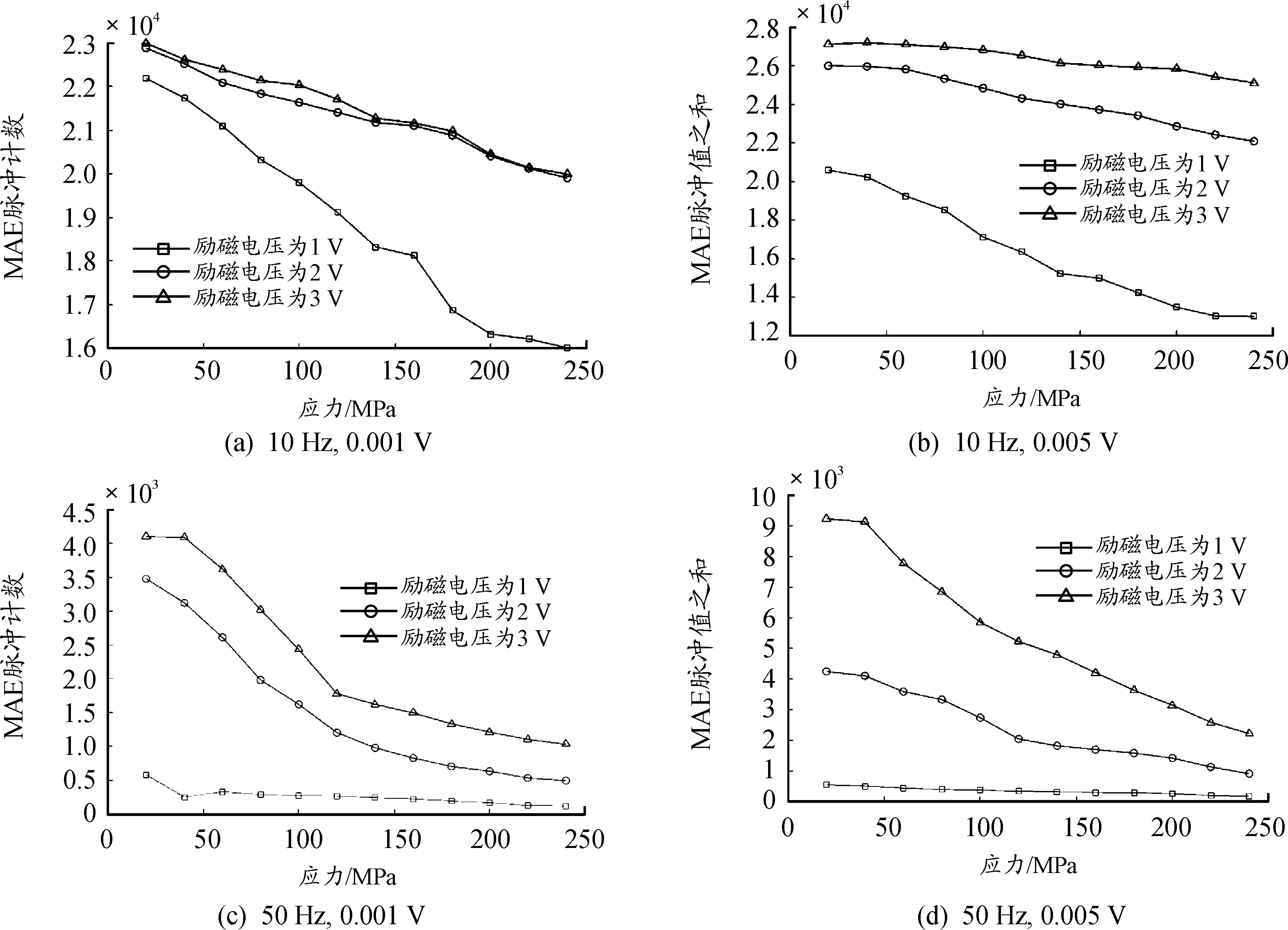
图11 不同励磁频率及门槛值电压时，MAE的脉冲计数-应力曲线

图12 不同励磁频率及门槛值电压时，MAE的脉冲值之和-应力曲线

随着应力的增大，MAE的脉冲计数和脉冲值之和逐渐单调下降。对于磁声发射的脉冲计数，其应力的变化不仅与频率、励磁电压相关，还受门槛值的影响。当门槛值较高时，励磁电压越高，脉冲计数随应力的变化速率越大。励磁电压高于2 V时，脉冲计数随应力的变化速率几乎保持不变，但是脉冲计数值仍然继续增大。

对于脉冲计数之和，当门槛值较低时，在各个励磁电压下其变化速率几乎相同，不受励磁电压的影响。然而当励磁频率为10 Hz，励磁电压大于1 V时，同一应力状态时，随着励磁电压的增大，脉冲计数几乎保持不变。励磁频率为10 Hz、门槛值0.001 V时，脉冲计数随应力的最大变化率为28%左右(励磁电压为1.0 V)，脉冲值之和的最大变化率为38%左右；门槛值为0.0005 V时，脉冲计数的变化率为80%左右，脉冲值之和变化率为80%左右。励磁频率为50 Hz，门槛值0.001 V时，脉冲计数随应力的最大变化率为35%左右(励磁电压1 V)，脉冲值之和的最大变化率为40%左右；门槛值为0.005 V时，脉冲计数的变化率为70%，脉冲值之和的变化率为80%左右。由此可知，当门槛值为0.005 V，励磁电压为3 V时，脉冲计数和脉冲值之和对应力的变化更为敏感。

然而，当固定励磁频率不变，励磁电压大于1 V的时候，随着应力的增大，MAE信号的包络形状逐渐发生变化。如图13所示，随着应力的增大，尽管MAE信号强度降低，但是MAE包络的对称性增加，双峰逐渐明显。

图12 励磁频率为10 Hz,励磁电压为3 V时，不同应力下的MAE信号波形

4 结论

1) 基于能量守恒的力-磁耦合模型分析Q235静载拉伸下的电磁信号变化规律；外加的拉伸力使试件受力面积小的部分出现最大应力。当应力大于试件的屈服强度时，出现局部塑性变形，这种重复的塑性应变驱动疲劳裂纹的产生，从而使试件断裂。

2) 基于应力-磁导率模型，可以得到试件在不同应力状态下的磁导率。通过对试件进行磁导率的循环赋值，可以模拟试件的应力状态，随着应力的增大，消耗的功率也逐渐增大，此时导致释放的MAE能量变小。

3) 实验表明，在弹性范围内，随着应力的增大，正弦波励磁得到的MAE信号的均方根电压、包络面积、脉冲计数以及脉冲值之和均显著下降，但驼峰形信号的双峰特征更加显著。