多股簧非典型损伤建模研究
2020-10-12丁传俊吴永国
丁传俊,尹 强,高 焓,吴永国
(长安工业集团公司, 重庆 400023)
多股簧是由多股钢丝拧成钢索绕制而成的圆柱螺旋弹簧。和普通单股弹簧相比,多股簧抗冲击性能好、吸振能力强、具有较大的刚度和非线性阻尼、寿命长,常被用作小口径自动武器的缓冲复进簧。由于多股簧主要承受冲击载荷,多次循环使用后其性能将会发生变化,因此开展多股簧性能变化特性研究对自动武器的科学使用和故障预测具有重要意义。
在多次循环载荷作用下,多股簧的性能退化和损伤会引起弹簧静、动态力学性能的改变,从而影响相关机构的动力学特性[1-2]。雷松[3]研究了多股簧的扭动微动磨损机制,认为随着扭动循环次数的增加,钢丝间的接触应力和剪切应力均会增大,其中剪切应力增大的更为明显,从而导致更大的簧丝磨损量;张明明[4]使用气锤对多股簧进行了连续冲击试验,发现连续冲击400次后多股簧加载后半段和卸载前半段的静态刚度分别增大了18%和28.2%;田志峰[5]对某35 mm高炮的复进簧进行了多轮射击考核试验,试验结束后发现该多股簧自由长度的平均缩短量为37.5 mm (-6%),静压至某高度时弹簧回弹力的平均衰退量为55.75 N (-8%)。虽然以上研究取得了较好的成果,但当前并没有适用于多股簧性能变化的模型可用,迫切需要一种基于试验数据的性能计算模型或评估方法。
本研究基于某小口径自动炮拨弹板簧的静、动态测试数据,对比和分析了该多股簧使用4 000次前后的静、动态响应特性,并尝试性地定义多股簧的性能退化和非典型损伤;其次,通过提出多股簧非典型损伤量的分离办法,在使用Slip-Lock损伤单元的同时,提出非典型归一化迟滞模型的一般性构造方法并发展了两种损伤单元模型;通过使用参数辨识方法对损伤模型进行参数求解,本研究发现基于BWBN模型的Slip-Lock损伤单元模型和本研究构造的10参数损伤单元模型精度较高,而简化的5参数损伤单元模型参数较少,比较适合于工程上的应用。
1 静、动态试验结果分析
静态和动态试验分别使用万能拉压试验机和动态疲劳试验机进行测试。两根性质相同的多股簧被安装在上、下夹持件(板)之间(含有预压量),并穿过各自的导杆以防止在加载过程中发生弯曲;下夹持件(板)在试验过程中保持固定,上夹持件(板)通过试验机夹头(横梁)施加位移;多股簧的变形量为上夹头(板)的位移,恢复力通过试验机上的传感器测得;为了降低加载过程中摩擦力的影响,导杆在测试前清洗并涂上轻质润滑油。受实验条件限制,本研究中静态和动态试验的最大加载速度分别为:0.8 mm/s和214.9 mm/s。
图1即为测试结果,其中的n为循环加载次数。从静态测试结果(图1(a))中可以看出,4 000次使用前后弹簧的静态刚度差别不大,但弹簧在加载换向的部分区域里出现了损伤点,在损伤点之后,弹簧的静态刚度没有变化,但恢复力有一定的下降;动态响应曲线显示,多次发射后不仅多股簧刚度、响应曲线包络面积(耗能)发生了变化,而且损伤点更加明显。表1对发生变化的动态响应特性进行了对比:多股簧加载时的线性刚度有所增加,卸载时的线性刚度增大一倍以上;多股簧回弹力明显下降、响应曲线包络面积增大;加载减速和卸载减速时的损伤点比较明显,损伤点A、B两处恢复力的下降量分别为15.8 N和10.1 N,经过损伤点后响应曲线出现了恢复力的损伤区域。

图1 多股簧试验曲线

表1 发射4 000次前后的多股簧动态响应特性
基于以上试验结果的分析,本研究拟定义多股簧的“性能退化”为多股簧回弹力下降、迟滞耗能增大;由于多股簧多次加载后的表现有别于建筑结构的损伤表现,因此本研究拟定义多股簧的“非典型损伤”为多股簧振动换向前后出现的恢复力突变(即出现损伤点)。
许多实验和分析表明[2-4],多股簧性能退化的主要原因是随着循环使用次数的增加,钢丝之间的间隙区域减少,实际摩擦接触区域增大,因此导致弹簧响应曲线包络面积增大、回弹力下降;同时由于持续的加工硬化和塑性变形,多股簧的自由长度和弹簧螺距均会减小,而弹簧的非线性渐硬特性随射弹数增加而增强。
2 非线性响应模型
2.1 归一化Bouc-Wen迟滞模型
Bouc-Wen模型及其修正模型作为一种光滑的现象模型可以很好地反映多股簧的动态非线性特性。精简参数后的归一化Bouc-Wen迟滞模型[6]为:
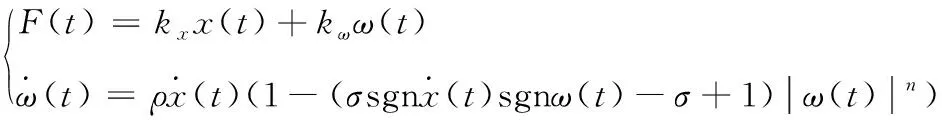
(1)
式中:F(t)为弹簧的恢复力;x、t分别为位移和时间;kx、kω分别为屈服后刚度系数和迟滞部分初始刚度;ω为纯迟滞部分,对于任意的x和t,都有|ω(t)|≤1;ρ、σ、n为控制纯迟滞部分ω(t)曲线形状的迟滞三参数。
2.2 修正的归一化Bouc-Wen迟滞模型
为了获得多股簧系统的非对称响应曲线,Zhao等[7]提出使用非线性刚度系数和非线性放大因子来代替归一化模型中的线性屈服后刚度系数和迟滞部分初始刚度,两者均用多项式表示:

(2)
式中:FE和FA分别是恢复力的非线性弹性部分和非线性放大部分;kEi和kAi分别是非线性刚度系数和非线性放大因子,N是多项式的阶数,一般取2阶或3阶。
从而得到可以描述多股簧动态响应的修正归一化Bouc-Wen迟滞模型(简称BW模型):

(3)
对于归一化Bouc-Wen模型,由内部损耗引起的纯迟滞部分ω(t)是有界的,且稳定在[-1,1]范围内,同时Zhao等[7]已经证明当输入量x关于0对称时,纯迟滞部分在ω-x平面内关于原点对称。图2(a)即为本文基于式(3)所预测的多股簧恢复力,图2(b)为与其对应的迟滞环。
3 损伤量的提取和损伤模型的构造
3.1 损伤量的提取过程
研究发现,多股簧性能退化后,其非线性弹性系数和非线性放大因子均会有较大改变,而纯迟滞部分参数变化较小,因此在最初的计算中,可以用无损伤多股簧的迟滞三参数来研究多股簧的损伤,当初步获得损伤单元的基本参数后可以使用迭代算法再进行参数的总体优化。损伤模型参数识别之前需要分离出损伤量,具体过程可以分为两步:第一,基于试验结果和识别算法,应用无损伤多股簧BW模型计算纯迟滞部分ω0(t),其结果如图2(b)所示;第二,基于损伤弹簧的试验数据分离出受损的纯迟滞部分ω(t),然后和无损伤的迟滞量相减得到损伤单元Δω(t)。

图2 多股簧的响应曲线和预测的归一化迟滞环
产生无损伤的迟滞环比较简单,这里将着重叙述提取损伤单元的第二步。由第二节所述的BW模型特性可知,当多股簧变形量足够大时,迟滞环中远离两端的部分将为±1,即为“有界区”,因此“有界区”内远离损伤点的纯迟滞部分可以写为:
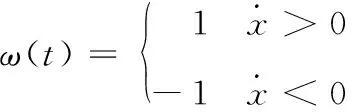
(4)
“有界区”内远离损伤点的恢复力为:
(5)
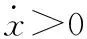
由于实际测量数据为一组离散的测量值,因此将式(5)写成离散形式:
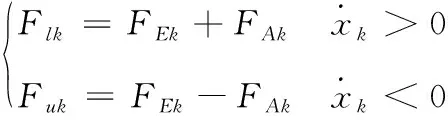
(6)
式中,下标k为一组测量数据中的第k个数据点。
远离损伤点且处于有界区域内的Fu和Fl如图3所示。
则远离损伤点的非线性弹性系数kE、非线性放大因子kA可以通过构建以下线性最小二乘优化问题求解:
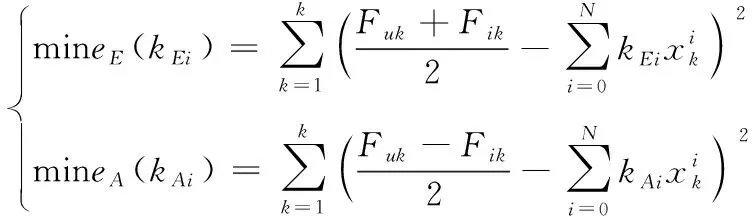
(7)
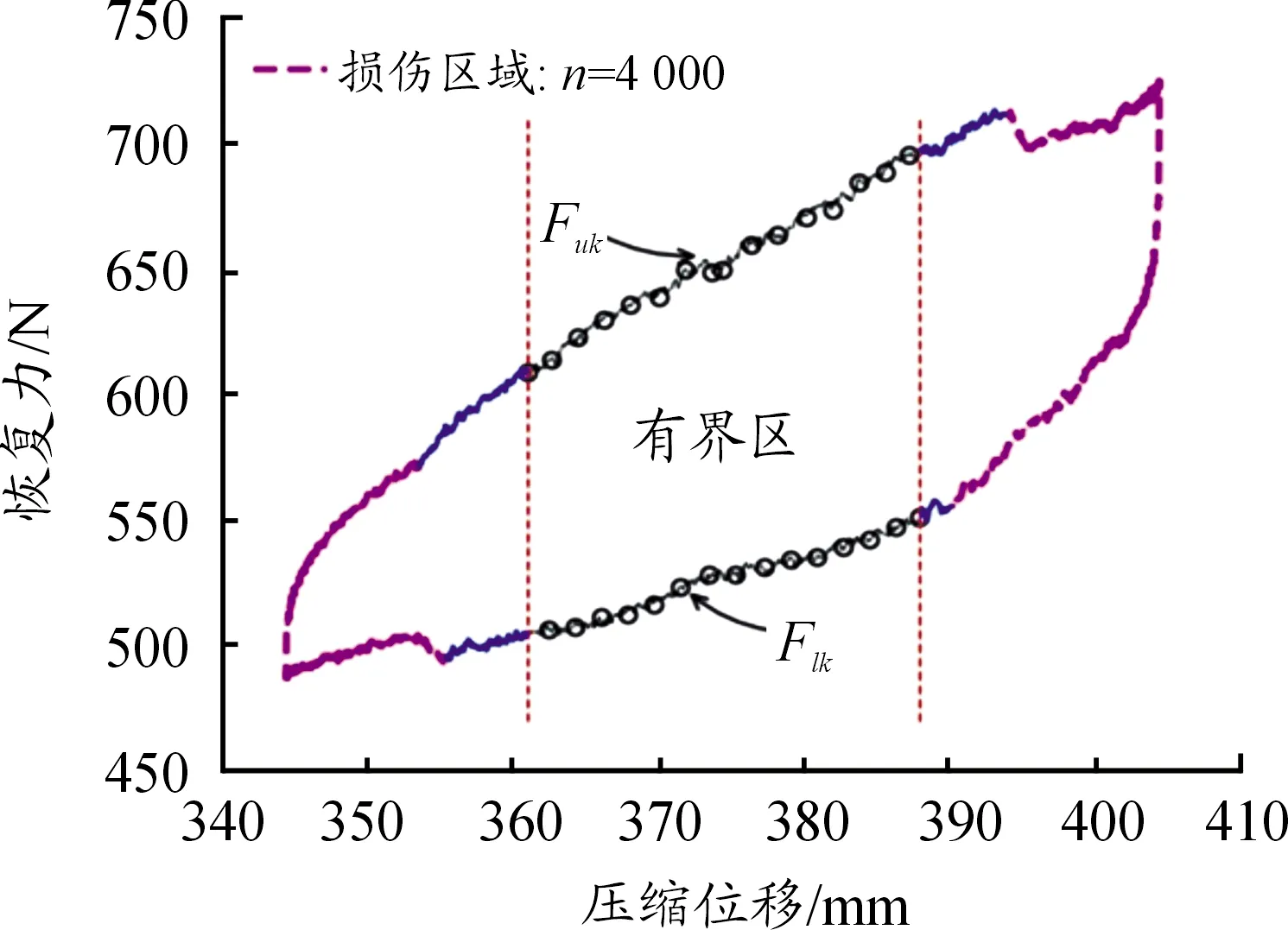
图3 多股簧响应曲线
最终,基于受损多股簧的测试数据将纯迟滞部分提取为:
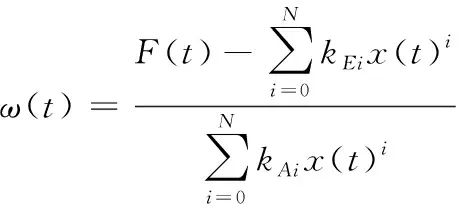
(8)
为了方便编程求解,将式(8)改写为离散形式:
(9)
图4即为上述过程提取出来的纯迟滞部分和损伤单元。从其中可以看出,和无损纯迟环相比,受损后的迟滞环也存在着两个明显的损伤点,这和多股簧恢复力曲线的表现是一致的。

图4 损伤前后迟滞量曲线
将无损伤的迟滞量和受损的迟滞量相减得到损伤单元:
Δω(t)=ω0(t)-ω(t)
(10)
如图4所示,损伤单元在一定区域内其值基本为0,而在加载和卸载的两端其取值范围是(-1,1);在多股簧加载减速和卸载减速时,损伤量存在突变。基于以上分析,本文总结损伤单元的两个特性:第一,当输入量x关于0对称时,基于归一化BW模型的损伤单元是关于原点对称的;第二,损伤单元Δω(t)的取值范围是(-1,1),且损伤量的变化与多股簧加载位移、速度有关。
3.2 Slip-Lock损伤单元
当建筑物受制于循环加载的非弹性变形时,结构的刚度和强度将会发生退化。Baber和Noori基于BW模型提出了BWBN模型[8],作为一种广义迟滞模型,BWBN模型增加了滑移-锁定单元(Slip-Lock element)用来模拟捏拢效应,其中捏拢滞回系统的迟滞量可以分解为两部分,一部分由光滑变形部分x1(t)控制,另一部分通过Slip-Lock单元的变形x2(t) 控制。
描述捏拢效应迟滞部分的微分模型为:
(11)
式中:A、β、γ、n分别为控制迟滞形状的基本参数;s、σ分别用来控制损伤滑移区间的长度和迟滞量的峰值。总体来说,Slip-Lock损伤单元的控制参数有6个,分别为:A、β、γ、n、s、σ,详尽的控制参数意义和敏感性排序可以参考文献[9]。
为了方便求解,可以将上面的耦合方程改写:
(12)
3.3 光滑损伤单元模型及其简化模型

常用的迟滞算子有双曲正弦函数、双曲正切函数和指数函数等,其表达式为:

(13)
式中:aj、bj、nj均为迟滞算子的系数。因此总体而言,对于任意非典型迟滞响应的纯迟滞部分,其微分模型可以表示为:
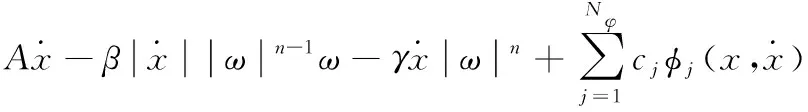
(14)
式中:cj和Nφ分别为所添加滞回算子的系数和个数。有必要说明的是,通过组合一定数量的滞回算子和确定相关的系数,这种方法所构造的迟滞模型介于参数化模型和非参数化模型之间[13-14],其原因在于这种方法所确定的模型参数没有清晰的物理意义且参数数量取决于计算所要求的精度。例如,本研究在模拟多股簧损伤单元时组合了式(13)中的3个算子,一共10个参数(简称10P损伤单元模型),其式如下:
(15)
根据文献[13]中所述的关于欠参数模型和过参数模型评价标准,假如上述模型中的某个参数趋于零,则可以将该部分算子去掉并形成简化模型。
4 损伤单元的参数识别过程与分析
4.1 参数识别过程
多股簧BW模型和损伤单元模型的参数识别问题可以归结为非线性优化问题,常见的求解方法有滤波算法、粒子云算法、差分演化算法、最小二乘法、人工神经网络算法等。反向差分演进算法(ODE)作为差分演进算法的改进算法,具有较强的寻优能力和较高的求解效率,比较适合于当前中等维度的多股簧参数识别问题。
当多股簧系统采用三阶刚度系数时,BW模型待求解参数向量p为:
p=[kE0,kE1,kE2,kE3,kA0,
kA1,kA2,kA3,ρ,σ,n]
(16)
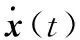
(17)
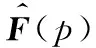
损伤单元的参数求解过程和上面类似,使用Slip-Lock单元和10P损伤单元时的待求解参数向量分别为:
pSL=[A,B,γ,n,s,σ]
(18)
p10P=[A,B,γ,n,c1,n1,c2,a2,c3,a3]
(19)
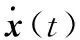
设置种群大小为5倍的求解参数数量,交叉率Cr=0.5,最大允许迭代次数Gmax=5 000,迭代终止条件为成本函数的最大最小值之差小于1.0E-6,算法框架采用Rahnamayan等[14]所介绍的抗噪声ODE框架,反向操作的跳转率Jr=0.3。
4.2 参数辨识结果分析
迭代收敛之后,分别使用Slip-Lock单元和10P损伤单元参数来预测多股簧的损伤量和力/位移响应,其结果如图5和图6所示。观察二者的力/位移响应曲线,可以看出,除了无法很好地捕捉恢复力突变外,以上两个损伤单元模型均能很好地匹配试验结果。虽然Slip-Lock模型参数生成的损伤单元可以捕捉到损伤量的突变,但在位移的加载和卸载换向处,Slip-Lock损伤单元曲线过渡不光滑、存在尖角(右下角),而且所预测损伤量的中段直线部分稍稍有些倾斜,不为0,这和实际情况是不符的;构造的10P损伤模型作为一个光滑的模型,能在各个区段内很好地符合试验结果,但10P损伤单元不对称,这显然是试验数据本身的不对称性造成的。
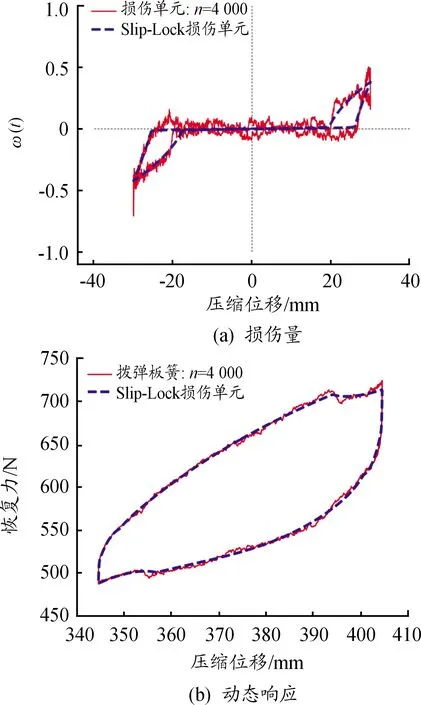
图5 Slip-Lock单元的预测曲线
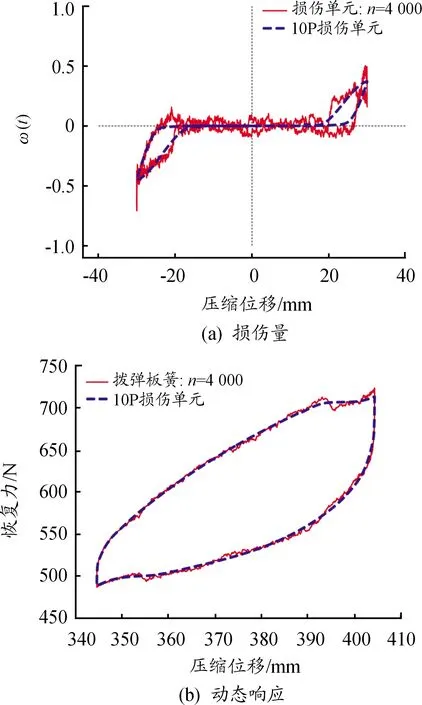
图6 10P损伤模型的预测曲线
通过多次计算并查看10P损伤模型所辨识出来的多组参数,发现有些组参数中的部分参数差别较小、部分算子系数趋于0,这说明10P损伤单元是一个参数过定义模型。比如,当A和γ的值相近时,n的值会趋于0;如果设定n1=2时,c3和a3的值将会趋于0。鉴于此,本研究基于10P损伤模型给出5P简化损伤模型:

(21)
基于5P模型的参数辨识结果如图7所示,可以看出简化模型作为一个对称模型,除了不能很好地捕捉损伤量的突变之外,在其他的各个区段都能很好地匹配试验曲线,这一点也体现在所预测的力/位移曲线上。

图7 5P简化损伤模型的预测曲线
采用以上各种模型的参数辨识结果如表2所示。直接使用修正归一化BW模型对受损多股簧的响应曲线进行参数辨识并不能获得理想的结果,这凸显了构造损伤单元模型的意义。

表2 4种模型的预测精度
5 结论
1) 多股簧在多次循环使用后,不仅其非线性刚度、响应曲线包络面积(耗能)发生变化,而且出现损伤点,损伤点前后多股簧恢复力存在突变。
2) 基于归一化BW模型的多股簧损伤单元作为一种非典型迟滞响应,其值在(-1,1),可以通过本文提出的分离办法将其分离,并构造合适的迟滞模型求解。
3) 基于BWBN模型的Slip-Lock损伤单元和本文构造的10P损伤模型都可以很好地预测多股簧非典型损伤后的响应,而简化的5参数损伤单元模型参数较少,比较适合工程应用。
