有向切换拓扑条件下多无人机系统抗扰动编队-追踪控制

2020-10-12赵学远周绍磊王帅磊祁亚辉

兵器装备工程学报 2020年9期

赵学远，周绍磊，王帅磊，祁亚辉

(海军航空大学，山东烟台 264001)

随着无人机技术的发展，以及战场环境的变化，多无人机系统的编队控制问题逐渐成为了学者们争先研究的领域[1-2]，在近年来涌现出了丰硕的成果，如文献[3]研究了带有时延的多智能体系统的编队控制，所设计的控制器能够有效控制智能体形成期望编队。文献[4]提出了一种基于人工力场的控制方法，使得无人机在飞行过程中在虚拟力场作用下，形成期望的编队。而随着多智能体一致性理论的研究，将一致性应用于多无人机编队控制当中的成果越来越多，而一致性编队控制问题的解决反过来给一致性理论成果的发展提供了很大帮助[5-7]。

在无人机飞行过程中，极容易受外外界阵风的扰动，这类扰动具有随机产生、短时有界的特点，其对多无人机系统编队的控制品质造成了一定的问题，因此如何抑制这类短时有界扰动，提高系统的鲁棒性极具有实际意义。而在现有文献中，多是针对已知扰动或常数扰动进行的讨论，如文献[8]考虑了常数扰动存在时异构多智能体系统的一致性问题，所设计的控制器只能抑制常数扰动，对随机产生的外界扰动并不能有效抑制。文献[9-10]则都是针对已知扰动设计的控制器提高智能体系统鲁棒性。

虽然也有部分文献针对未知外界扰动展开研究，如文献[11]为带有时延的非线性多智能体系统设计了一致性控制器，有效抑制了一维白噪声干扰。文献[12]设计了H∞控制器，使得多智能体系统抵抗外界短时有界扰动影响，实现了系统的一致性控制，并借助线性矩阵不等式给出了一致性控制器的设计步骤。但是上述文献中系统的通信拓扑结构均为固定的拓扑结构，但是无人机之间距离增大、障碍物阻挡等外界环境变化极易造成多无人机系统的通信拓扑结构发生变化。而固定拓扑条件下所得到的结论不能直接应用于有向切换拓扑体条件，因此降低对多无人机系统的通信拓扑约束，研究有向切换拓扑条件下的抗扰动问题更具有实际意义。

在无人机飞行过程中，会根据执行任务不同将无人机分为领导者和跟随者，在战场环境中，不仅需要多无人机系统形成期望编队，还希望编队能够追踪期望轨迹，因此多无人机系统的编队-追踪控制问题更具有研究价值，其中领导者追踪期望轨迹，跟随者形成期望编队。

本文针对有向切换拓扑条件下的多无人机系统编队-追踪控制问题展开研究，考虑无人机在飞行过程中受到外界短时有界扰动，设计H∞控制，实现了多无人机系统的编队-追踪控制，并对扰动由一定的抑制作用，满足了暂态性能指标，提高了系统的鲁棒性。

1 相关引理

引理1[13]图G的Laplacian矩阵L至少有一个零特征值，其他非零特征值均具有正实部；如果有向图G包含有一个有向生成树，则0是L的简单特征值，1N是其对应的右特征向量。

引理2[14]若矩阵W∈RN×N的所有特征值均具有正实部，那么存在一个正定矩阵Q使得

WTQ+QW>2αQ

其中0<α

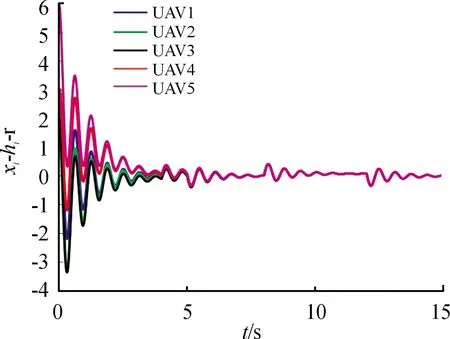
2 问题描述

考虑多无人机系统中的无人机由二阶动力学系统模型描述，在飞行过程中无人机受到阵风影响，阵风具有短时有界且随机产生的性质，这与文献[8]中的常数扰动和文献[9-10]中的已知扰动具有很大不同。第i架无人机的动力学模型可刻画为：

(1)

根据无人机执行任务不同，将负责追踪编队中心轨迹的无人机称为领导者，其他形成编队的无人机称之为跟随者。领导者无人机序号为1，跟随者无人机序号为2,…,N。

(2)

为了行文通顺，在此给出平均驻留的定义。

定义1：随着时间任意切换的多无人机系统内部通信拓扑结构图Gσ(t)，在给定时间区间[t0,t)的平均驻留时间为

其中NB(t0,t)是多无人系统通信拓扑图在时间[t0,t)内的切换次数。

3 一致性控制器设计

分别为领导者和跟随者设计如下控制器

(3)

将领导者的控制器代入1号无人机可得

(4)

定义领导者实际状态与编队中心轨迹误差为θ1(t)=x1(t)-r(t)，因此可以得到

(5)

(6)

将跟随者的控制器代入2,…,N号无人机可得

(7)

令

ξ(t)=[ξ2(t),ξ3(t),…,ξN(t)]T可得

(8)

其中

θi(t)=xi(t)-hi(t)，i=2,…,N

(9)

定义：多无人机系统在形成期望编队的过程中，如式(3)的控制器可使系统实现满足暂态响应性能的H∞一致性控制，能够有效抑制外部短时有界扰动，如果对于给定的扰动衰减指标γ>0，系统满足如下两个条件：

1) 当w(t)=0时，对于任意对给定的无人机初始状态

(10)

2) 当w(t)≠0时，初始状态为0时，多无人机系统的性能指标满足

(11)

基于上述分析给出有向切换拓扑条件下控制器的设计步骤及对步骤设计合理性的证明。

步骤1选取反馈矩阵K1使得(A+BK1)是Hurwitz的，且式(11)成立。

步骤2选取常数0<α

步骤3求反馈矩阵K2=-BTP2。

(12)

其中σ是大于1的常数，P1为正定对称阵。

(13)

其中，φ1=max(λ(Q))，φ2=min(λ(Q))，γ>0给定常数。

证明：由于作为领导者的1号无人机在多无人机系统的通信拓扑图中，只能向跟随者传递信息，而不能接收来自跟随者的信息，因此拓扑图的切换过程不会对其产生影响。

针对领导者构造Lyapunov函数

(14)

对式(14)求导可得

(15)

(16)

其中

根据Schur补引理可得，当且仅当式(12)成立时，Φ<0显然成立

因此

(17)

对两端同时积分可得

(18)

对于零初始条件可得

(19)

当w=0时，

(20)

对式(14)沿着式(20)求导可得

(21)

针对跟随者，多无人机系统的通信拓扑结构发生变化会对其产生影响，因此构造分段的Lyapunov函数如下

(22)

对其求导可得

2wT(t)(FTQσ(t)⊗DTP2)θ2n

(23)

2wT(t)(FTQσ(t)⊗DTP2)θ2n

(24)

当w≠0时，

(25)

那么

(26)

(27)

其中

Θ2=Qσ(t)F⊗P2D

因为Qσ(t)≤φ1I,FFT≤φI，则

ATP2+P2A-2αP2BBTP2+βP2+

(28)

故可得

(29)

因此ϑ(t)>0，故恒成立

(30)

(31)

因此对两端同时积分可得

(32)

因此对于零初始条件可得

(33)

因为ϑ(t)=eσk(t-tk)，那么1<ϑ(t)<μ，故

(34)

当w=0时，

(35)

对式(22)沿着系统(35)求导可得

(36)

由式(13)可得

ATP2+P2A-2αP2BBTP2+βP2<0

(37)

结合式(37)和式(36)可得

(38)

故

V2(t)

(39)

(40)

对式(39)和式(40)进行迭代计算可得

V2(t)≤e-βtμkV(0)

(41)

(42)

综上按照所给步骤设计的控制器能够实现多无人机系统的编队-追踪控制，并满足暂态性能指标。

4 仿真验证

将无人机考虑为由式(1)描述的二阶模型，假设无人机三维空间运动相互解耦，多无人机系统的通信拓扑在图1中随机切换，在图2中展示多无人机系统通信拓扑图的切换过程。

图1 多无人机系统通信拓扑示意图

图2 拓扑切换过程曲线

从拓扑图图中可得到相应的Laplacian矩阵，因为拓扑切换过程只对跟随者产生影响，故为了简便，在此只给出跟随者之间的拓扑结构对应的Laplacian矩阵

设无人机受到的短时有界扰动函数为

其中

通过步骤1可求得

通过步骤2可求得

通过步骤3可求得

如图3所示为无人机在t时刻无人机实际位置与期望编队和编队中心轨迹考虑暂态响应的误差量曲线，由定义可知，当误差量趋向于0时，领导者在编队中心准确跟踪轨迹r(t)，跟随者形成期望的平行四边形编队.从图3中发现经过3 s的振荡，误差量基本收敛于0，开始在0附近微小振荡，且当4～5 s和8～12 s外界干扰作用下，振荡幅度较小，尤其是在8～12 s期间，可以说对外界扰动抑制效果非常明显，只在扰动产生(8 s)和扰动结束(12 s)时产生了很小的振荡，对多无人机系统形成期望编队并追踪轨迹影响甚微，满足了暂态性能指标。