基于可拓学理论的传感器选型优化研究

邢 鹏，贾希胜，郭驰名，王双川

(陆军工程大学 装备指挥与管理系， 石家庄 050003)

近年来，随着现代武器装备信息化、集成化和智能化程度的不断提高，武器系统的可靠性、安全性和经济性等问题日益突出，故障诊断和预测以及维修保障等方面越来越受到人们的重视。目前，大多数武器装备仍以事后维修和定期维修为主，不仅存在着较大的安全隐患，并且费用高昂。故障预测与健康管理(prognostic and health management,PHM)系统对提高复杂武器系统战备完好率和可用性具有重要意义，作为信息收集最重要、最基础的手段，传感器选取是否恰当是武器装备PHM系统中故障诊断和故障预测能力的决定性因素[1]。

目前，国内外研究人员对于传感器系统在航空航天、高铁、桥梁、煤矿、建筑等领域研究较多。美国宇航局研究中心开发的系统传感器选择策略(S4)[2]，描述了一种基于模型的，为指定系统健康评估选择传感器的过程，对其助推级火箭发动机上的应用进行了介绍；Manohar Shamaiah等[3]利用贪婪传感器选择算法研究了资源受限传感器网络中的传感器选择问题，用仿真实验证明了此方法具有更好的性能；唐勇等[4]构建多传感器表决冗余系统，将遗传算法应用到桥梁基础传感器系统的优化过程中，既保证了系统的可靠性，也达到了减少费用的目的，但该研究重点在传感器配置位置和数量上进行优化；杨志刚等[5]通过气压爆破测试中频率响应范围和幅值的比较，提出对于高速列车过隧道过程中，远、近场测试时传感器选型的具体要求，但缺少通用的选型方法；张亚运[6]为实现桥梁的线性监测设计了一套双轴倾角传感器系统，给出了传感器优化配置的常用方法，但并未对传感器怎样选型进行论述；万亚旗等[7]为解决高温井下可燃气体检测问题，对多种原理的传感器进行对比分析，通过分析各自的优缺点，给出最终选型方案，但同样缺少科学的选型方法；尹训强等[8]介绍了传感器优化配置的准则、算法的研究进展，并对其发展趋势进行了展望。

本文基于现有防空导弹发射车起竖系统一体化模型[9]，将可拓学理论应用于起竖系统传感器的选型过程中，具有一定的指导和借鉴意义。

1 可拓学理论[10-11]

可拓学是把矛盾问题作为研究对象，用形式化的模型探究事物拓展的可能性及开拓创新的规律和方法。可拓学的基本理论是可拓论，其以基元为逻辑细胞，通过建立矛盾问题的可拓模型，研究基元的基本性质、解决矛盾问题的集合论基础和推理形式，把解决客观世界的矛盾问题转化为定性和定量后的基元之间的关系问题。可拓论有3个核心部分：基元理论、可拓集理论和可拓逻辑。

1.1 物元理论和可拓集理论

根据基元理论，描述事物基本元包括了物元、事元和关系元，针对传感器选型这一问题将应用物元理论，它的表达式为有序的三元组R=(N,c,v)，其中：N表示事物名称，c表示其特征，v表示N关于c的量值。

若R为多维物元，则一个物有多个特征及其对应的量值，ci(i=1,2,…，n)是特征向量，vi(i=1,2,…，n)是特征向量对应的量值,多维物元可以用所构成的矩阵列表示：

(1)

根据可拓集定义，设U为论域，若x是U中任意元素，则U中的可拓集A定义为

A={(x,y);x∈U,y=k(x)∈(-∞,+∞)}

(2)

式中：y=k(x)是可拓集A的关联函数，k(x)是将U中每个元素映射到区间的关联度。

1.2 关联函数值计算

关联函数值的计算可以采取以下这种方法进行，设X0=〈a,b〉,X=〈ap,bp〉，X0∈X，则初等关联函数为

(3)

式(3)中：X0表示经典域，X表示节域，ρ(x,X0)表示经典域下某一元素的关联函数值，D(x,X0,X)表示节域下某一元素的关联函数值，其函数关系式可以表示为

(4)

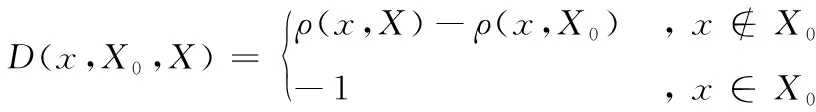
(5)

1.3 可拓学理论在多方案优选中的应用

为在多备选方案中选择理想的方案，可设F={F1,F2,…,Fm}为备选方案，则物元模型可以表示为

(6)

式(6)中：Fi表示第i种方案，Cj(j=1,2,…,n)表示待评方案的影响特征，Vij表示第i种方案对应于Cj的量值，即从专家处收集到的具体数据。

为能评价多备选方案是否能满足要求，需要给出理想方案的物元模型，可以表示为

(7)

式(7)中：F*表示理想方案；Cj表示待评方案的影响特征；Vj表示理想方案的对应于Cj的量域，Vj=〈aj,bj〉为关于特征(C1,C2,…,Cn)T给定的范围，即经典域，可由决策人员根据实际应用情况确定。

在多备选方案的选型评价中，(C1,C2,…,Cn)T表示特征指标，(V1,V2,…,Vn)T表示决策人员给每项指标的评分，记Vpj=〈apj,bpj〉为特征集(C1,C2,…,Cn)T所容许的范围，即节域，可由决策人员对应的每个特征评分的最大量值范围确定。

由初等关联计算得到的待评价方案的关联函数表达式可表示为

(8)

式(8)中：Vj=〈aj,bj〉,Vpj=〈apj,bpj〉。

每一特征对于方案选取的影响程度并不相同，因此，若考虑特征值的权重问题，则备选方案与理想方案的关联度为

(9)

关联度能够反映选型方案与理想方案的接近程度，关联度越大，选型方案越接近决策人员预期。

2 防空导弹发射车起竖系统传感器选型可拓学分析

2.1 备选传感器选择[12]

从合适的众多的传感器中为起竖系统选择合适的备选传感器，主要包括以下几个步骤：

在决策人员为PHM系统选择传感器之前，必须要了解应用对象分系统和部件的操作，而后进行故障模式及影响分析FMEA，明确装备的功能、故障模式、故障原因和故障影响，从而为传感器的选取提供基本信息。

PHM系统要实现其诊断和预测功能依赖于传感器掌握基本的测量参数，通常情况下，选择传感器必须符合特定的规范和标准，例如，对某装备发动机进行数据监测，在选择传感器时，需要满足发动机工作环境中温度、湿度等要求，另一方面，提取的数据应在传感器的量程范围之内，符合相应的敏感度要求。

对系统的接口、输入输出形式和参数、安装方式、安全性、可靠性和经济性等明确具体要求。

通过以上步骤对PHM选择传感器进行备选之后，可以保证该系统按预期目标运行，为后期理想方案的确定提供了较好的备选基础。

2.2 建立物元模型[13]

根据防空导弹发射车起竖系统的特点和传感器主要选型参考标准，从应用的实际情况出发，以传感器特性、精度、性能、可靠性、经济性、适应性为评价因素建立评价指标体系[14]，建立可拓分析的模型，可以表示为

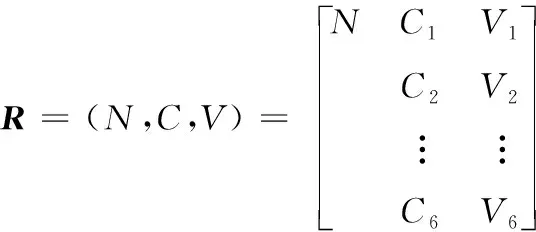
(10)

式(10)中：N表示通过本章第1节筛选的备选传感器，C=(C1,C2,…,C6)T=(传感器特性、精度、性能、可靠性、经济性、适应性)T,V=(V1,V2,…,V6)T表示决策人员对备选传感器六项指标给出的评分值。

2.3 层次分析法确定各指标权重系数值

权重系数的取值对于方案的选择具有十分重要的作用，不同权重系数很大程度上会得到不同的方案。将影响选型的因素分解为两个层次，建立层次分析模型，如图1所示。该模型由评价对象、一级指标和二级指标组成。评价对象为传感器选型，一级指标为传感器特性、精度、性能、可靠性、经济性、适应性，仅用六个一级指标对传感器进行评价过于笼统宽泛，因此，针对不同的一级指标建立二级评价指标。

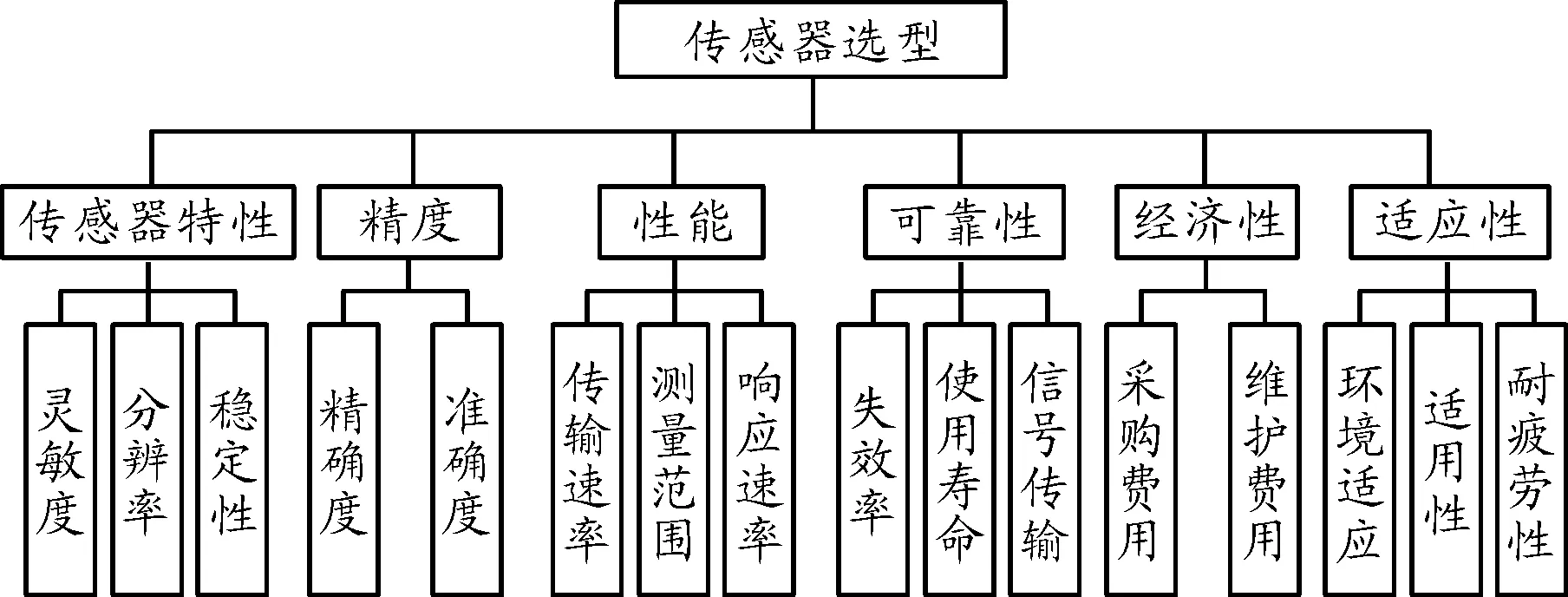
图1 传感器选型评价指标层次结构模型框图

构造层次模型之后，需要进一步确定每个指标对传感器选型的影响程度，可以通过在各层指标之间按照一定的标度原则两两进行量化比较，构造出判断矩阵：

(11)

式(11)中：Wi表示第i个因素对应于上一层次中指标的重要性的权重。设aij=Wi/Wj,则可以得到aij有如下性质：

(1)aij=1(i=j;i,j=1,2,…,n);

(2)aij=1/aji(i≠j;i,j=1,2,…,n)。

根据9/9～9/1标度法[15]，对备选传感器的6个一级指标影响因素两两比较后构成判断矩阵可以用式(12)表示：

(12)

利用Matlab计算得出每个一级指标影响因素的权重系数矩阵Wa为

Wa=[0.147 1, 0.168 0, 0.214 3,

0.168 0, 0.116 3, 0.186 3]T

(13)

经计算，判断矩阵A的最大特征值λmax=6.018，满足一致性要求。

同理，分别构造二级指标判断矩阵，并进行一致性检验，可以得到各二级指标权重，分别为

Wb=[0.318 3, 0.267 5, 0.414 1]T

Wc=[0.431 5, 0.568 5]T

Wd=[0.331 7, 0.375 1, 0.293 3]T

We=[0.328 1, 0.263 6, 0.408 4]T

Wf=[0.351 5, 0.648 5]T

Wg=[0.293 3, 0.331 7, 0.375 1]T

由6个一级指标和16个二级指标构成传感器选型权重系数值，如表1所示。

3 实例分析

对于导弹发射车起竖系统而言，通常要求振动加速度需小于2g，否则，其引起的冲击会对导弹上的敏感元件造成损坏。除此之外，在发射车行军和发射架竖起的过程中，它的振动频率通常不超过200 Hz[16]，根据这些要求及2.1节中备选传感器选型的基本步骤，将可能状态信息进行采集，选用了美国Endevco三种不同型号的振动传感器，有关参数如表2所示。

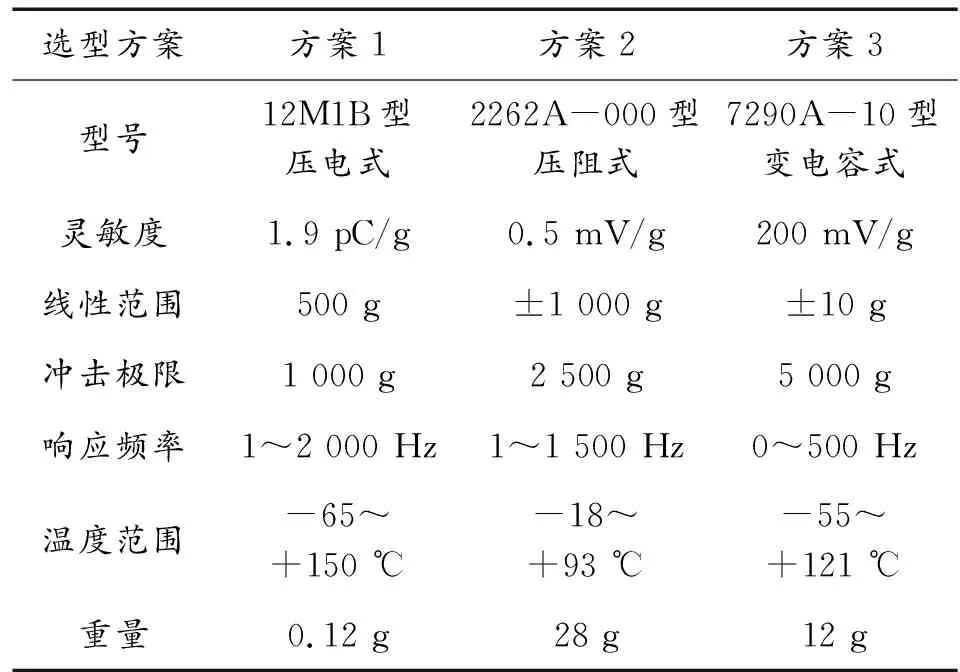
表2 振动传感器参数

将传感器选型评价指标分发给专家，要求其按照第2节中列出的6个1级指标和16个2级指标对3种备选方案按照百分制进行打分，收集后的结果如表3所示。

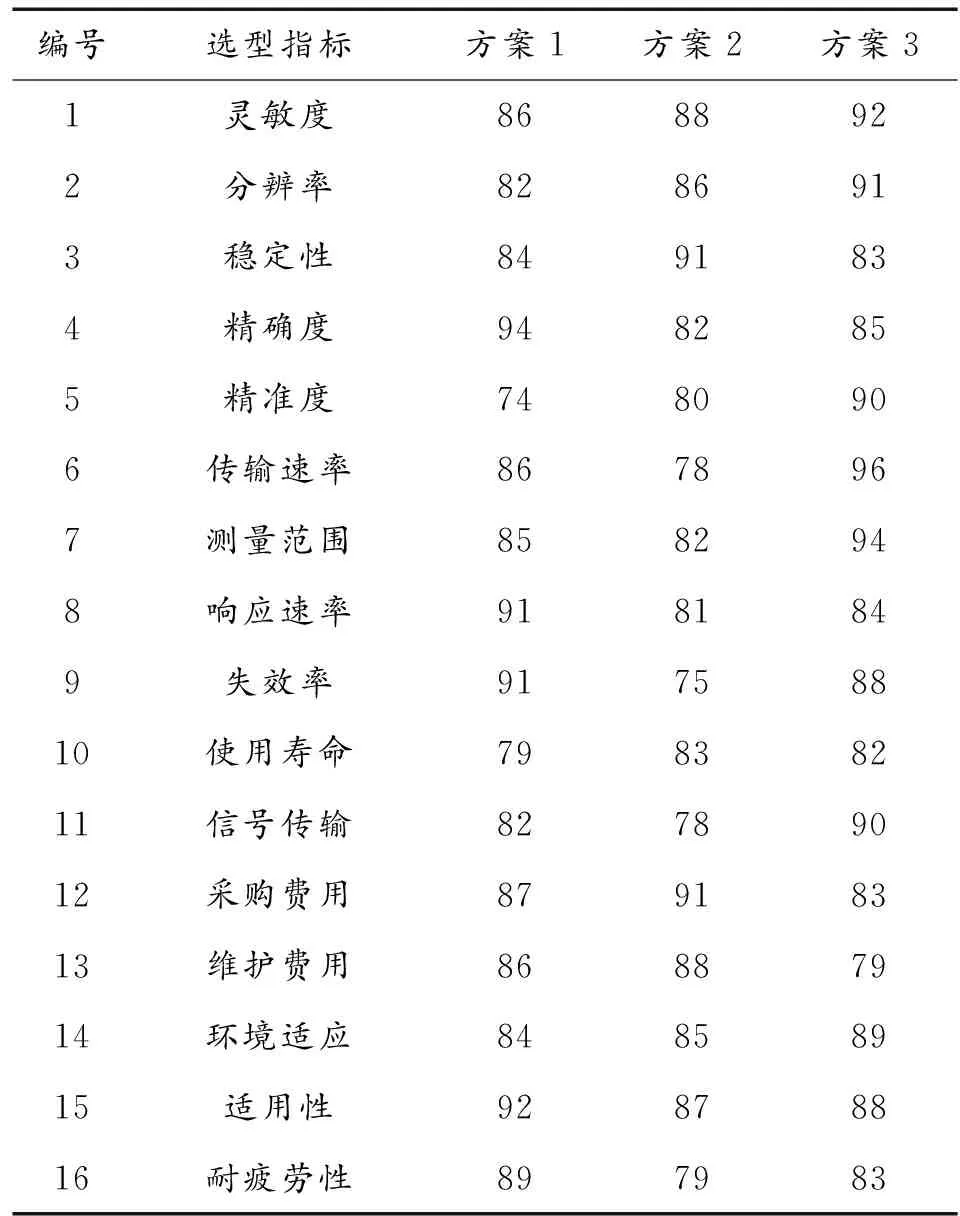
表3 备选传感器量化评分表

根据专家评分值，备选方案中物元模型期望的量值范围和可能的最大量值范围，即经典域和节域如下所示：

经典域：

V1=〈80,95〉,V2=〈85,95〉,V3=〈80,95〉

V4=〈80,95〉,V5=〈75,95〉,V6=〈80,95〉

V7=〈75,95〉,V8=〈80,95〉,V9=〈75,95〉

V10=〈80,95〉,V11=〈75,95〉,V12=〈75,90〉

V13=〈80,95〉,V14=〈85,95〉,V15=〈85,95〉

V16=〈80,90〉

节域：

V1p=〈80,100〉,V2p=〈80,100〉,V3p=〈70,100〉

V4p=〈90,100〉,V5p=〈90,100〉,V6p=〈85,100〉

V7p=〈70,100〉,V8p=〈80,100〉,V9p=〈80,100〉

V10p=〈70,100〉,V11p=〈80,100〉,V12p=〈80,100〉

V13p=〈90,100〉,V14p=〈80,100〉,V15p=〈80,100〉

V16p=〈70,100〉

根据式(4)和式(8)得到方案1中关联度评价计算方法为：

(13)

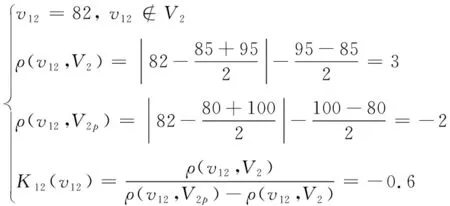
(14)

同理可得出：K13(v13)=4，K14(v14)=1，K15(v15)=0.067，K16(v16)=6,K17(v17)=10,K18(v18)=4,K19(v19)=4,K110(v110)=-0.1,K111(v111)=7,K112(v112)=3,K113(v113)=6,K114(v114)=-0.2,K115(v115)=3,K116(v116)=1。

因此，由关联度的大小得到在本算例中振动传感器备选方案的最优顺序为：方案1、方案3、方案2。通过模糊优先排序法对本实例进行验证，得出结果与采用可拓论的方法一致，验证了本方法的可行性。

4 结论

运用可拓学理论与层次分析法对某防空导弹发射车起竖系统的传感器选型进行了分析评价，得到较为理想的选型方案。从众多的传感器中为所应用的系统或部件选择合适的备选传感器，采用可拓学理论中物元和关联函数的概念，结合层次分析法确定的权重值，将影响传感器选型的因素用定性和定量的方式结合起来，通过具体算例说明了运用可拓学方法对传感器选型进行评价具有较好的可行性和操作性。