一种带航迹角约束的临近空间目标拦截中制导算法

2020-10-12许志，史伟，唐硕

宇航学报 2020年9期

许志，史伟，唐硕

(1. 西北工业大学航天学院，西安 710072；2. 陕西省空天飞行器设计重点实验室，西安 710072)

0 引言

临近空间高超声速武器具有大空域、速度快、机动性强等飞行特性，给防空系统的拦截中制导带来了新的挑战[1-5]，具体表现为：1)当低速的防空导弹拦截高速的临近空间飞行器时，中-末制导交班时导弹只有处于目标的逆轨状态时，才能有效降低末制导的需用过载[6]；2)弹-目以一定交会角碰撞可有效提高对目标的毁伤效果。同时当中-末制导交班时满足零控拦截条件时，可有效降低末制导段的拦截难度；3)防空导弹在临近空间飞行时可用过载有限，需要降低全程过载并保证终端过载收敛。上述特点使得防空导弹的中制导必需满足的约束是使导引头稳定捕获目标、有效降低中制导段的需用过载以及满足逆轨拦截的要求。

目前国内外学者多针对弹-目速度比处于优势条件下的中制导律研究，常用的设计方法有滑模导引律[7-8]、最优导引律[9-12]、比例导引法及其变形[13-14]等。文献[7]设计了一种满足控制能量最小和中末制导交班时速度前置角最小的最优滑模中制导律。文献[9-10]提出了一种满足终端位置与角度约束的中制导律，并在此基础上推导出II脉冲点火时刻。文献[13]推导了基于零控脱靶量的变系数预测比例导引法，并提出了剩余时间估计方法。上述方法主要是针对低速目标的拦截任务，临近空间目标特性打破了防空导弹的速度、过载优势，极快的弹-目相对速度导致这些方法难以保证多约束条件下的过载收敛性问题。并且，按照一定交会角拦截目标保证毁伤效果，更降低了这些方法的适用性。而针对目标的精确打击，在中-末制导交班时进入零控拦截流形，有效降低末制导的拦截难度，对中制导算法的设计具有重要价值。文献[15-17]研究了满足零控拦截条件下的弹-目相对运动关系，无法适用于满足特定航迹角约束条件下的零控拦截流形解算。

本文以具有双脉冲发动机的防空导弹拦截临近空间高超声速目标为拦截场景，在文献[11]的基础上改进推导了一种保证终端过载收敛的ZEM-ZEV制导律，基于文献[15-17]设计了三维带航迹角约束的零控拦截流形，并以此为中制导终端约束，改进了上述制导方法无法适用于对交会角的约束；通过在线动态生成的最优初-中制导交班速度方向与II脉冲发动机开机时刻，进一步降低中制导段的需用过载，满足飞行时间约束。

1 防空导弹多约束问题

防空导弹采用姿、轨控发动机与双脉冲发动机的方案来提高拦截能力，典型飞行时序如图1所示。在攻防双方的飞行特性要求下，防空导弹中制导算法面临新的困难与挑战：

1)采用逆轨拦截的方式增加了中-末交班约束条件。由于极快的弹-目相对速度，有效攻击区十分狭窄，需要拦截弹具备航迹角、视线角速率约束的逆轨拦截条件，大大增加了中制导技术难度。典型末制导的拦截条件如图2所示，由于导引头视场、机动能力等限制因素，末制导段的捕获域急剧减小，对中-末制导交班时的速度偏差要求苛刻。因此将防空导弹导引至带航迹角约束的零控拦截流形是最有效的中制导方式之一。

2)初-中制导交班条件约束。拦截弹采用姿、轨控发动机的方案来提高初制导转向能力，当交班条件超出范围时，导弹需要付出较大过载才能调整飞行状态，这会使得拦截弹在临近空间无法提供足够的过载而导致脱靶。

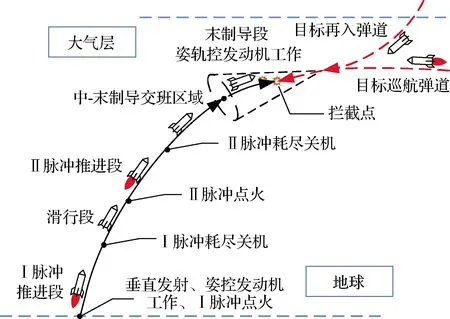
图1 典型防空导弹飞行时序示意图Fig.1 Typical launch process of a interceptor

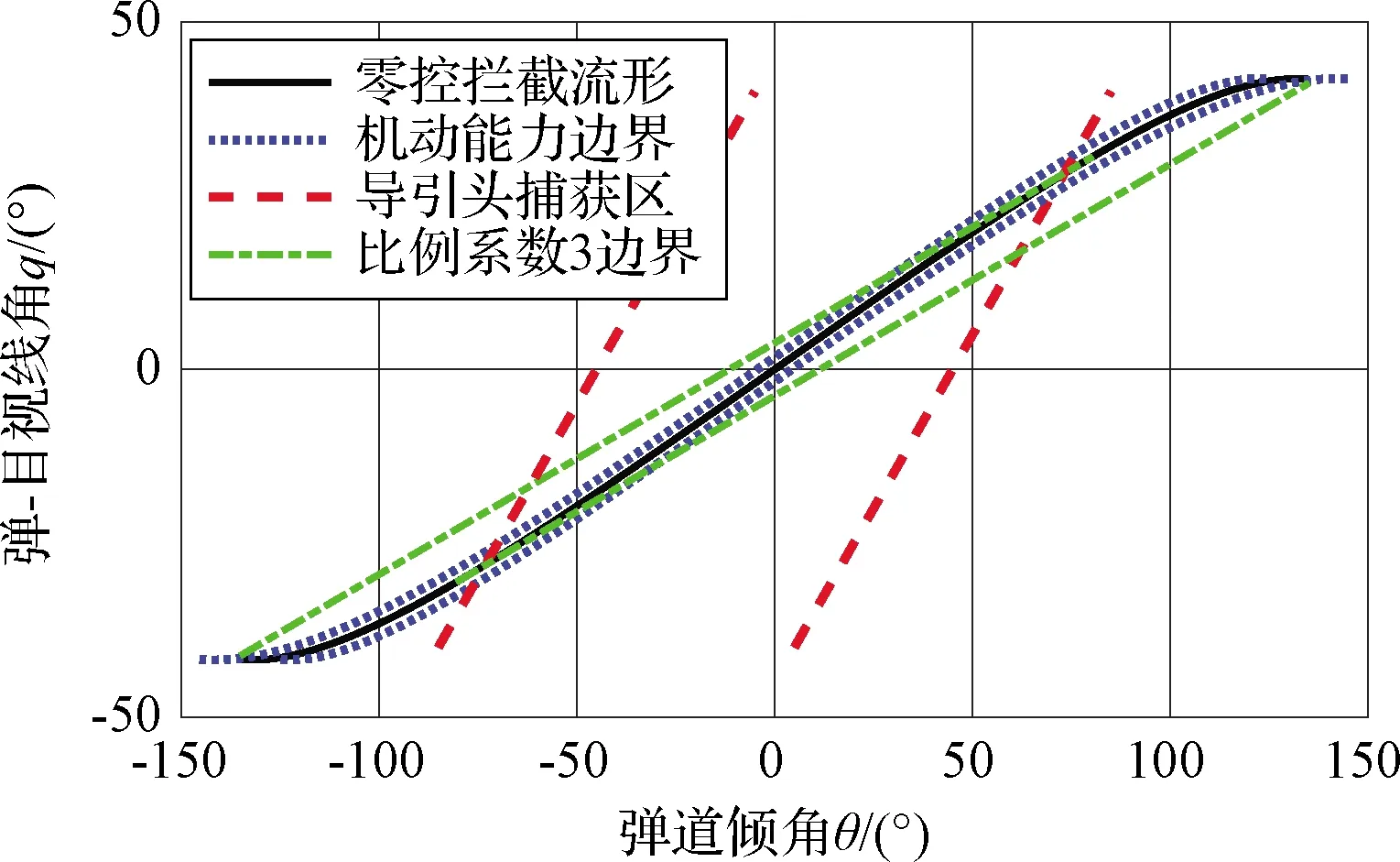
图2 典型末制导拦截条件Fig.2 Typical terminal guidance interception condition

3)可调II脉冲发动机开机时刻成为重要的中制导设计参数之一。II脉冲发动机开机时刻决定拦截弹的动力分配，影响全段飞行时间，使拦截弹具备动态调整弹-目遭遇点的能力。

由图2可知，防空导弹需要采取逆轨拦截方式才能保证对临近空间高超声速目标的拦截效果。因此本文从以下几个方面开展工作：首先，利用最优控制原理推导满足多约束的中制导律；其次，设计带航迹角约束的零控拦截流形，并作为中-末制导交班约束；最后，在剩余时间高精度估计的基础上，设计防空导弹初-中制导交班条件与II脉冲发动机开机时刻的迭代逻辑，达到降低中制导段需用过载的目的。

2 多约束中制导算法

2.1 基于中-末制导交班约束的ZEM-ZEV制导算法

零控脱靶量(Zero-Effort-Miss，ZEM)定义为零过载条件下飞行器飞行至终端时的位置偏差；零控速度偏量(Zero-Effort-Velocity，ZEV)定义为零过载条件下飞行器飞行至终端时的速度偏差。基于中-末制导交班约束的ZEM-ZEV算法[11]研究制导指令与零控脱靶量、零控速度偏量的关系，具体推导如下。

在发射坐标系下的防空导弹质心运动方程为：

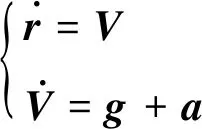
(1)

式中：r和V分别为是导弹的位置矢量和速度矢量，a是除重力外的合外力T(推力及气动力)产生的加速度，本文将其视为控制量。

设计带时变权重的全程控制能量最小为性能指标，可有效降低全程过载，并保证过载的收敛性：

(2)

引入中-末制导交班的位置矢量与速度矢量约束，作为中制导终端约束：

(3)

通过求解式(4)的两点边值问题可得制导律，引入拉格朗日乘子将终端约束与性能指标结合，有：

(4)

由式(4)可得，该性能指标对应的哈密尔顿函数：

(5)

式中：λr，λV分别为位置速度矢量r，V对应的协态向量。由变分法求解最优控制问题，可得：

(6)

由式(6)可得，控制量与协态向量的关系为：

(7)

式中：tgo=tf-t，表示剩余飞行时间。将式(7)得到的控制量解析模型带入式(1)质心运动方程，通过式(3)的终端约束可得最优控制的解：

(8)

进一步将重力加速度简化为常值，可得：

(9)

引入考虑重力加速度的零控脱靶量Rzem与零控速度偏量Vzev，有：

(10)

联立式(9)、(10)，可得制导指令与零控脱靶量、零控速度偏量的关系：

(11)

式(11)是基于中-末制导交班位置、速度约束的ZEM-ZEV制导算法，其核心思想是在飞行过程中修正预测位置、速度偏差来适应终端约束，是一种基于预测-校正的制导律。

2.2 带航迹角约束的零控拦截流形

将拦截弹送入至零控拦截流形可有效降低末制导的过载，是最有效的中制导方式之一。当弹-目距离较近时，可忽略重力加速度对零控拦截流形影响较小[15-17]。

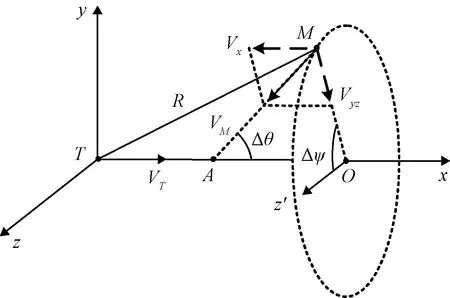
图3 目标弹道坐标系下的弹-目运动关系Fig.3 Missile-target motion relationship in target ballistic coordinate system

满足零控拦截条件的弹-目运动关系如图3所示，采用目标弹道系Txyz作为参考系，引入航迹夹角Δθ与航迹偏角Δψ可将弹-目运动分解为两个平面的运动：Tx-M组成的等效纵向平面和侧向平面Tyz。

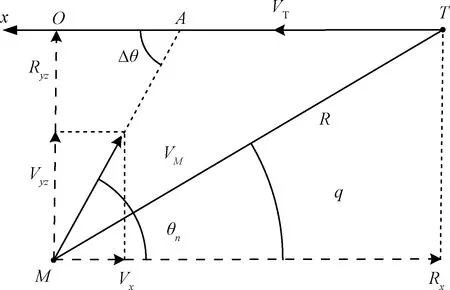
图4 在Tx-M面下的弹-目运动关系Fig.4 Missile-target motion relationship in Tx-M surface

等效纵向平面运动如图4所示，引入总视线角q与总弹道倾角θn可得，防空导弹的总弹道倾角为：

θn=Δθ

(12)

由弹-目运动关系可得碰撞三角形约束，可得满足零控拦截条件的总视线角与总弹道倾角关系：

(13)

因此，保证零控拦截条件的弹-目相对位置矢量与导弹速度矢量满足如下关系：

(14)

式(14)为Tx-M组成的等效纵向平面运动关系，保证了带航迹夹角约束下的零控拦截分布圆条件，需要引入侧向平面Tyz来描述分布圆上点的关系。

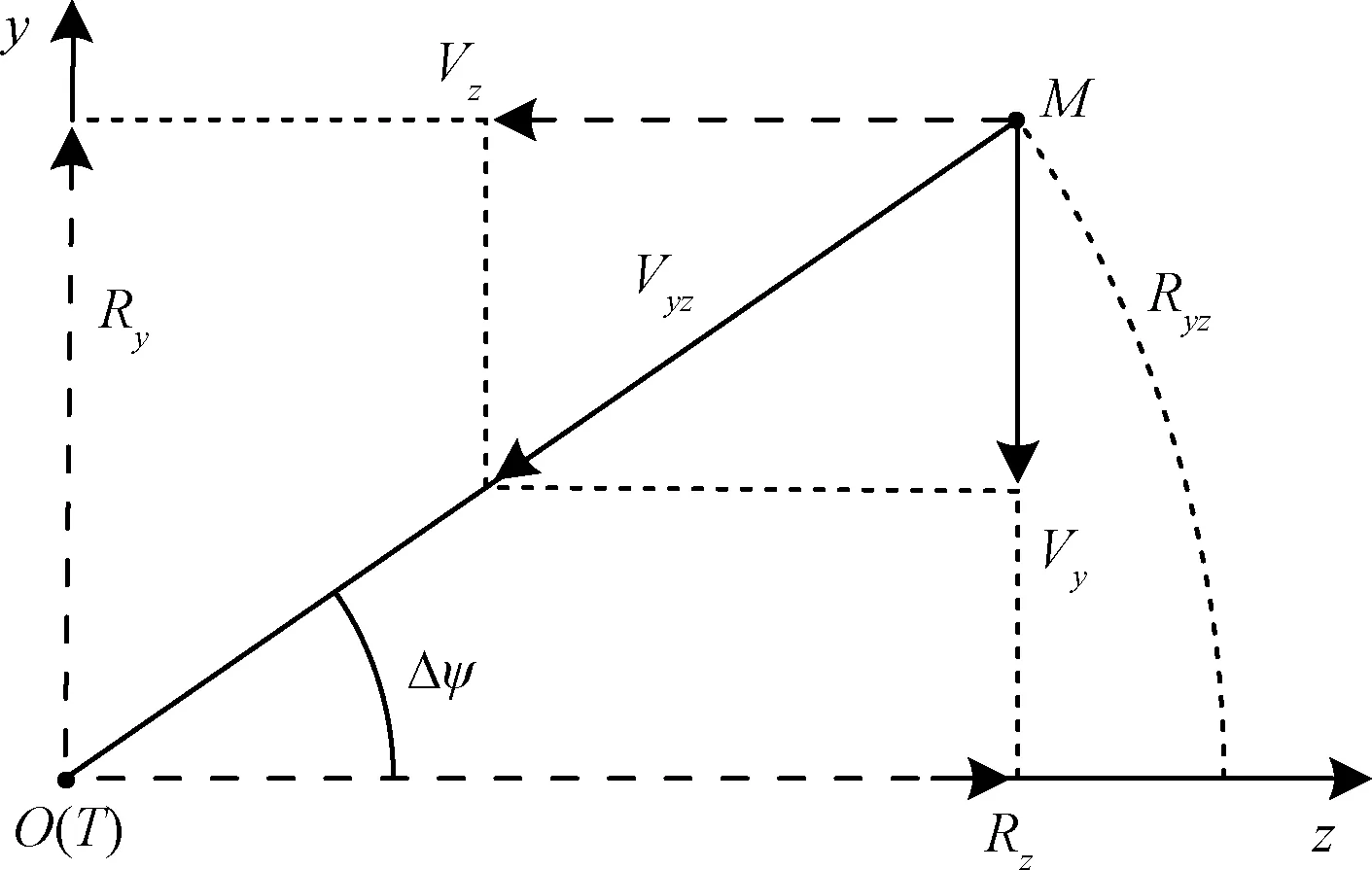
图5 在Tyz面下的弹-目运动关系Fig.5 Missile-target motion relationship in Tyz surface

Tyz面的弹-目相对运动关系如图5所示，弹-目相对运动在Tyz面的分量指向原点T可保证三维零控拦截条件：

(15)

联立式(14)、(15)，可得目标弹道坐标系下带航迹角约束的零控拦截流形，将上式转化为发射坐标系下，有：

(16)

式中：L(ψVT,θT)为发射系与目标弹道系的转换矩阵。式(16)是带航迹角约束的零控拦截流形，是防空导弹在中-末制导交班时需要满足的条件。

3 中制导算法求解

3.1 制导参数迭代算法

以带航迹角约束的零控拦截流形作为中制导终端约束，依靠当前飞行状态预测终端位置、速度偏差生成制导指令，是本文所提多约束中制导的核心思想，因此需要解算三项内容：剩余时间tgo、零控脱靶量Rzem、零控速度偏量Vzev。

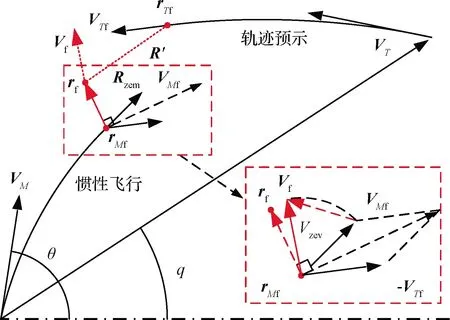
图6 ZEM-ZEV制导算法基本原理Fig.6 Basic principle of ZEM-ZEV guidance algorithm

制导参数的矢量关系如图6所示。将式(1)简化为关于法向过载n的拦截弹状态微分表达式，引入轨迹预示的目标状态微分表达式，组成弹-目运动状态方程：

(17)

式中：XM，XT分别为导弹与目标的运动学参量。将零控条件下的状态微分方程积分来预测未来防空导弹的飞行状态，有：

(18)

引入导引头探测距离R，当弹-目距离小于R时视为中-末制导交班完成。以附加零控拦截流形的目标预示信息作为时变中制导终端约束，即：

(19)

联立式(17)，(19)，积分至防空导弹距中制导终端位置最近时，作为迭代结束标志，即：

(VT f-VMf)·(rT f+R′-rMf)=0

(20)

式中：rMf，rTf分别是弹、目终端位置矢量，VMf，VTf分别是弹、目终端速度矢量，R′是带航迹角约束的零控拦截流形中距离矢量。由式(20)迭代终端时刻tf与当前飞行时刻t，可以得到中制导剩余时间高精度估算结果，即：

tgo=tf-t

(21)

因此，制导算法中的Rzem与Vzev分别为：

(22)

联立式(21)和(22)，可得制导算法中的剩余时间tgo，零控脱靶量Rzem，零控速度偏量Vzev。通过引入标称零控导弹运动模型与目标预示模型解算的制导参数，提高中制导剩余时间估计精度，保证终端偏差收敛至0。

3.2 交班参数及点火时间的计算

保证初-中制导交班平缓是降低中制导需用过载的必要条件之一。将采用直接力转弯后的弹体转向转化为速度转向，简化转弯后的初制导为零控飞行，因此初-中制导交班条件可转化为保证交班平缓的初始速度方向优化问题。本文根据研究对象的特性，利用具备实现容易、精度高、收敛快等特点的粒子群算法，设计初中制导交班点速度方向迭代逻辑。

以来袭目标的初始方向为射向，将初始弹道倾角与弹道偏角作为粒子群算法的控制量，即：

u=(θ,ψV)

(23)

引入式(11)的制导律，建立控制量与初-中制导交班处法向过载的关系：

(24)

以交班处的法向过载最小作为性能指标：

(25)

根据各个粒子的性能，计算个体最优位置pi,j与全局最优位置gj，根据粒子群算法进行迭代：

(26)

式中：r为更新粒子时所使用的随机数，c为全局最优与粒子最优所占比重。通过上式将粒子群不断迭代至满足精度要求为止，即：

(27)

在设计II脉冲发动机开机时刻时，通过引入剩余时间估算方法，以全段飞行时间偏差的指标来设计II脉冲发动机开机时刻，并引入牛顿迭代法作为迭代基本方法，有：

(28)

当II脉冲开机时间迭代至满足精度要求时，停止当前步骤迭代；当动态生成的开机时刻与飞行时间匹配时，II脉冲发动机点火。

4 逆轨拦截中制导算法的仿真验证

本文以某临近空间高超声速滑翔飞行器作为拦截对象，初始位置为(300 km，60 km，0 km)，初始速度3500 m/s，初始弹道倾角、偏角为(-22°，180°)，在临近空间作“S”形机动，飞行过程中伴随着大幅度机动减速。

4.1 标称条件下多弹拦截机动目标仿真校验

本文通过设置不同飞行时间与航迹角约束的飞行任务来校验算法对终端任务的适应性。假设目标轨迹预示准确，设计标称条件下的多弹组网拦截场景：三枚防空导弹相隔4 s发射，全程飞行时间88 s，按照不同航迹角进行组网拦截。同时引入预测比例导引法(PPN)与本文所提方法进行对比。

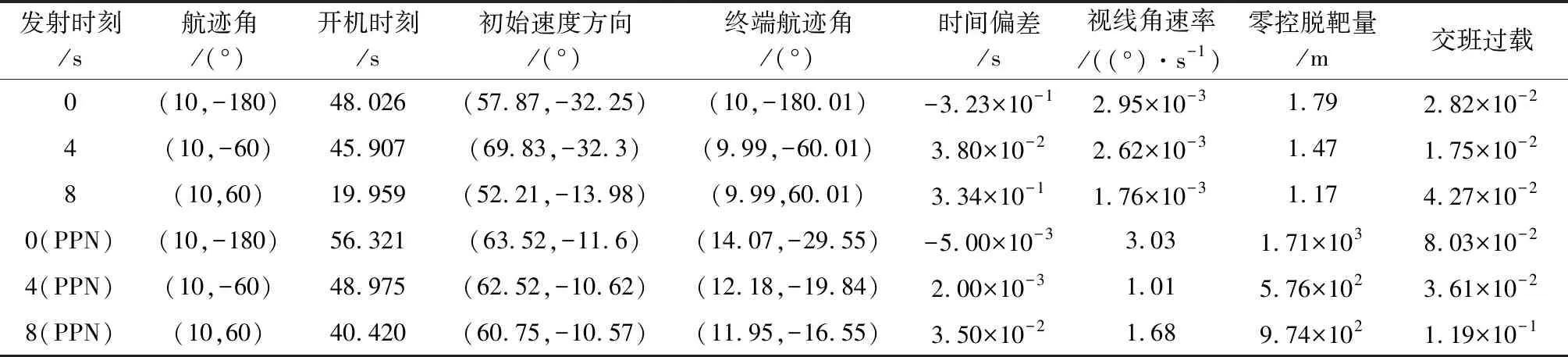
表1 标称条件下机动目标多弹拦截仿真结果Table 1 Simulation results of maneuverubf target mutielastic intercept under nominal conditions

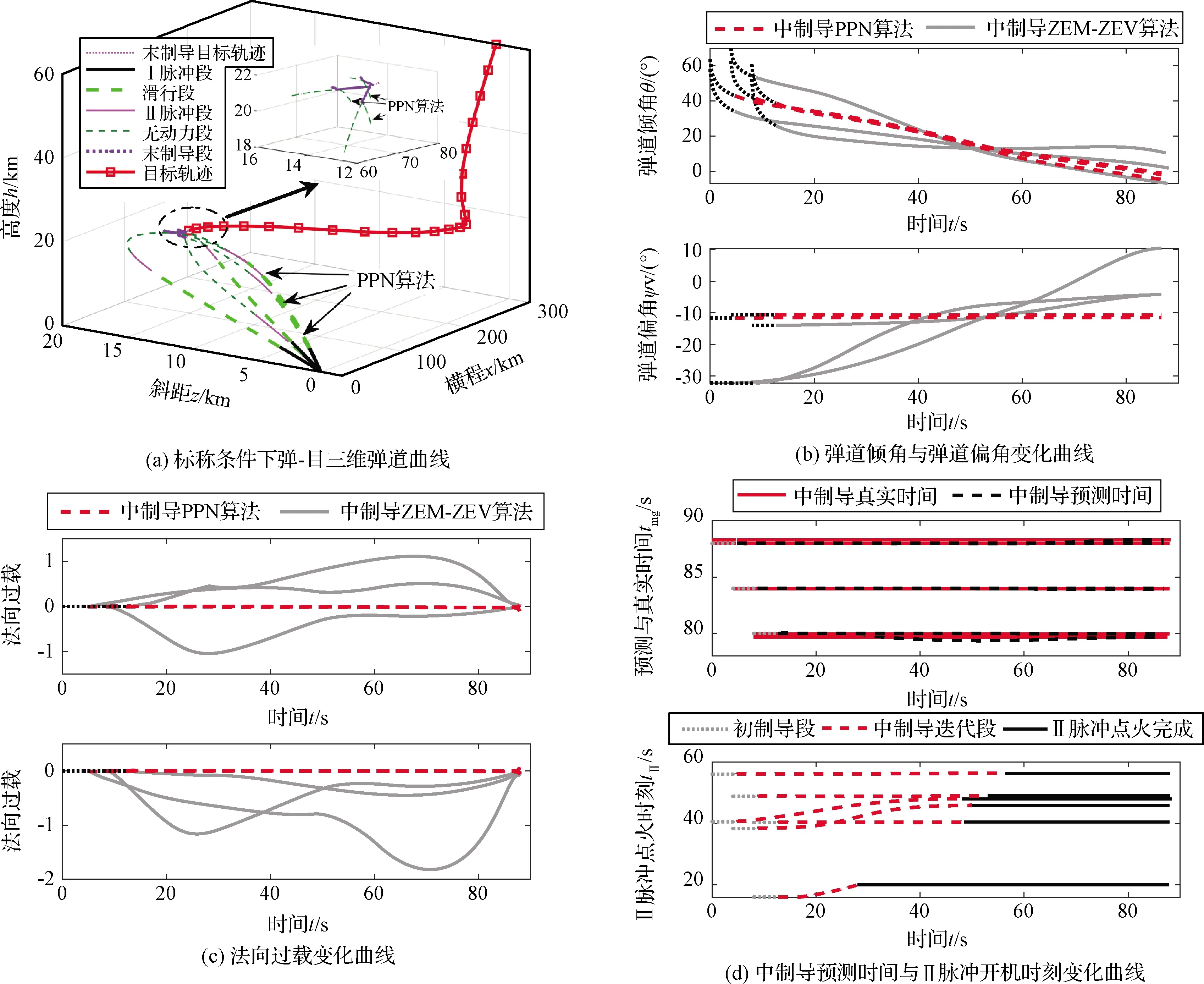
图7 机动目标无偏拦截飞行参数曲线Fig.7 Maneuvering target interception flight parameter curve under unbiased condition

标称条件下各项飞行参数的仿真曲线如图7所示。图7(a)飞行轨迹曲线中，两种算法的中-末制导交班点重合，但本文所提算法的脱靶量更小，表明本文所提算法保证将防空导弹送入零控拦截流形中，可有效降低末制导过载；图7(b)、(c)弹道方向与过载曲线中，设计的初始速度方向保证了初-中制导平缓交班，在降低全程过载的同时能够使过载具有收敛性，对比预测比例导引法具有明显优势；图7(d)预测飞行余时间与真实飞行时间重合，表明本文提出的剩余时间求解算法高精度地估算出中制导段飞行时间，根据拦截任务在线动态生成II脉冲发动机开机时刻。根据表1给出时间偏差、视线角速率、零控脱靶量等仿真结果可知，本文所提方法能够同时满足终端位置、速度方向与飞行时间约束，进而将导弹导引至带航迹角约束的零控拦截流形中，在有效降低中制导段需用过载的同时，保证了过载的收敛性。对比预测比例导引法，由于无法引入速度方向约束，会引起较大的脱靶量。

4.2 偏差条件下算法鲁棒性验证

为检验本文所提制导方法的制导精度及鲁棒性，针对防空导弹总体参数的偏差散布(如表2所示)进行Monte Carlo打靶方法仿真检验。引入偏差条件下的拦截场景：10 s时拦截弹按照解算的初始速度方向(53.56°，-17.38°)发射，以预定终端航迹角(10°,90°)拦截目标，通过动态调整Ⅱ脉冲发动机开机时刻来满足全程任务飞行时间(80 s)。

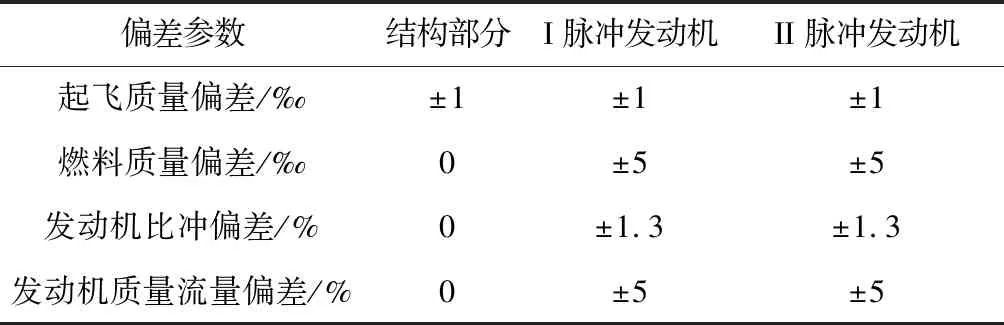
表2 防空导弹总体参数偏差配置表Table 2 Air defense missile overall parameter deviation configurationTable

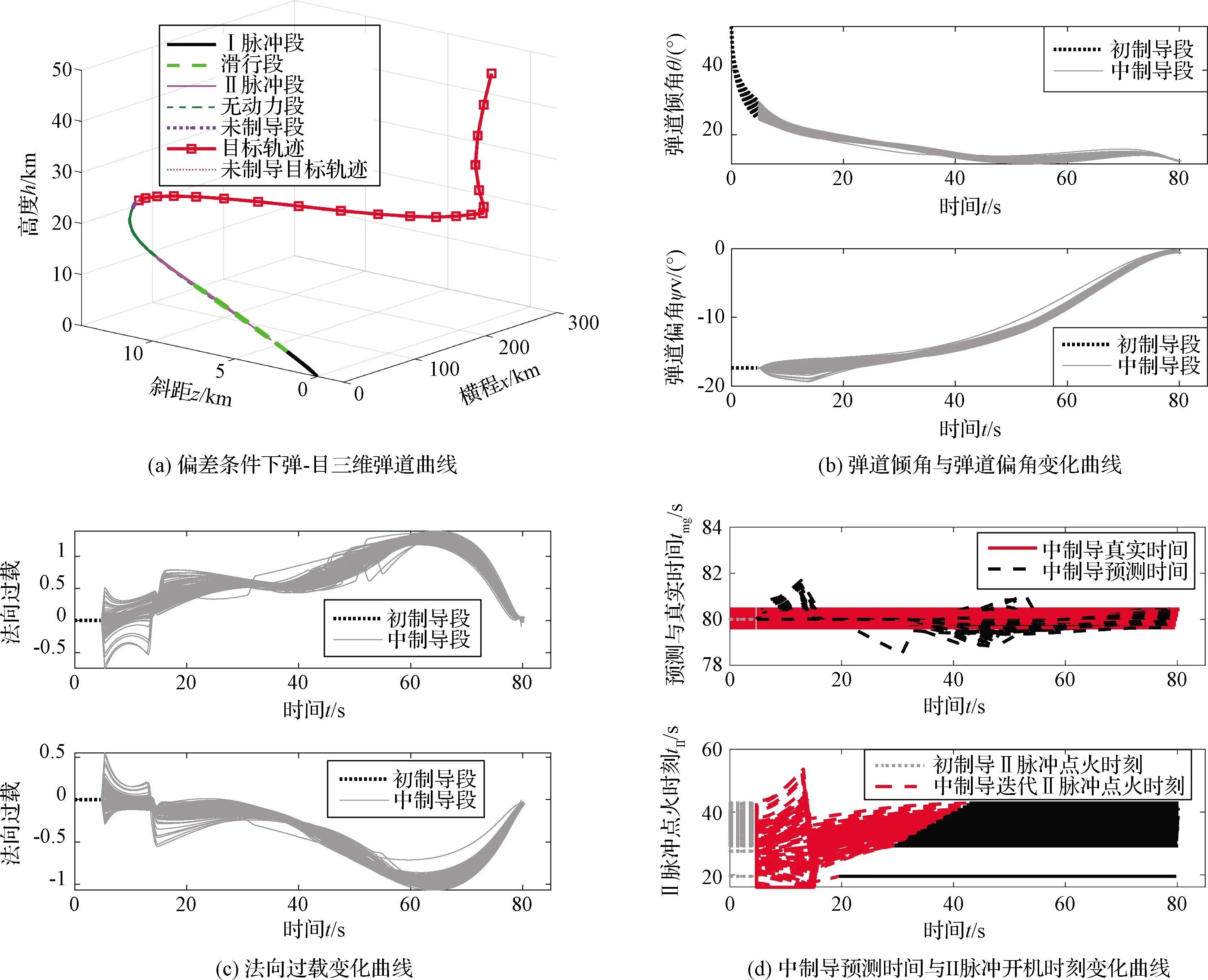
图8 偏差条件下机动目标拦截飞行参数曲线Fig.8 Maneuvering target interception flight parameter curve under biased condition

偏差条件下各项飞行参数的仿真曲线如图8所示，不同偏差散布下算法通过动态调节II脉冲发动机的开机时刻，保证飞行时间约束。由图8(b)、(c)可以看出在初-中制导交班点等典型飞行时刻的过载曲线出现较大阶跃，这是由于存在总体参数偏差，使用标称值解算制导参数时会带来额外的机动，但仍保证了在全程过载较小的前提下的终端过载收敛；图8(d)中制导预测飞行时间散布在±2 s以内，参数偏差降低中制导预测时间的精度，影响II脉冲开机时刻，但预测飞行时间偏差散布较小，仍旧具备重要的应用价值。

由表3给出统计结果可知，本文所提中制导算法对总体参数偏差具有强鲁棒性、制导精度高，在偏差条件下完成预定拦截任务。