基于一类二元多小波函数的密度估计

王淑媛 崔丽鸿

(北京化工大学 数理学院， 北京 100029)

引 言

密度函数估计是统计学中的一个基本问题。密度估计分为参数估计和非参数估计，对于后者，直方图估计、核估计以及k-近邻估计等都是研究的重点[1-2]。随着小波理论的完善，加上其具有诸如正交性、紧支性、多分辨分析(MRA)等优良特性，使得小波分析的应用成为近年来非参数统计与计量研究的热点。1988年，Doukhan[3]首先提出了小波密度估计的概念。随后，许多学者对此进行研究，并给出了收敛阶的证明[4-5]。但由于单小波不能同时满足正交性、对称性及紧支性，在实际应用中造成了很大困扰，基于此，双正交小波和多小波相继被提出。

Locke等[6]首次将多小波应用到密度函数估计中,并给出了估计器表达式，最后通过模拟实验对比了小波与多小波估计的结果。黄守勇等[7]给出了线性多小波密度估计的收敛阶及证明。本文基于文献[6]提出的多小波密度估计，结合吕军等[8]给出的一类二元多小波构造方法，提出了一类二元多小波密度估计，并证明其在积分均方误差(MISE)意义下存在收敛上界。仿真和实例数据的实验结果证明了方法和估计的可行性。

1 小波密度估计

1.1 二元单小波密度估计

φ(x,y)=φ(x)φ(y)

记

φj,k1,k2(x,y)=2jφ(x-k1,y-k2)

ψl,j,k1,k2(x,y)=2jψi(x-k1,y-k2)

式中，j为分辨率水平，k1、k2为平移参数，且j∈Z，k1,k2∈Z。

对任意的整数J>j0，j0∈Z，由多分辨分析定义[9]可知，二元实值函数f(x,y)∈L2(R2)在VJ空间的投影可展开为

ψl,j,k1,k2(x,y)

(1)

由尺度函数和小波函数的正交性可得

αj0,k1,k2=〈f(x,y),φj0,k1,k2(x,y)〉=∬f(x,y)·φj0,k1,k2(x,y)dxdy

βl,j,k1,k2=〈f(x,y),ψl,j,k1,k2(x,y)〉=∬f(x,y)·ψl,j,k1,k2(x,y)dxdy

由数学期望定义可得

αj0,k1,k2=∬f(x,y)φj0,k1,k2(x,y)dxdy=E(φj0,k1,k2(X,Y))

βl,j,k1,k2=∬f(x,y)ψl,j,k1,k2(x,y)dxdy=E(ψl,j,k1,k2(X,Y))

得到式(1)的样本估计为

(2)

1.2 一类二元多小波密度估计

多小波是一种特殊的小波，它的基函数由向量函数构成[10-12]。假设多尺度向量函数和多小波向量函数分别为

Φ=[Φ1,Φ2,…,Φr]T，r∈Z

Ψ=[Ψ1,Ψ2,…,Ψr]T，r∈Z

这里一类二元多尺度函数和一类二元多小波函数的构造采用文献[8]的方法，即

Φ(x,y)=Φ(x)φ(y)

记

Φj,k1,k2(x,y)=2jΦ(x-k1,y-k2)

Ψl,j,k1,k2(x,y)=2jΨl(x-k1,y-k2)

定义1r重的多分辨分析是L2(R2)中满足以下条件的闭子空间VJ的嵌套序列，即：

(1)Vj∈Vj+1，j∈Z；

(3)h(x,y)∈Vj⟺h(2x,2y)∈Vj+1，j∈Z；

(4)h(x,y)∈Vj⟺h(x-k1,y-k2)∈Vj，j∈Z，k1,k1∈Z；

(5)存在r个函数Φ1(x,y)，Φ2(x,y)，…，Φr(x,y)，使得{Φw(x-k1,y-k2)，1≤w≤r,k1，k2∈Z}是空间V0的标准正交基。

令Wj是Vj+1中关于VJ的正交补空间，则L2(R2)能分解为空间Wj的直和，即

故任意的二元实值函数f(x,y)∈L2(R2)在VJ空间的投影可展开为

(3)

由多尺度函数和多小波函数的正交性可得

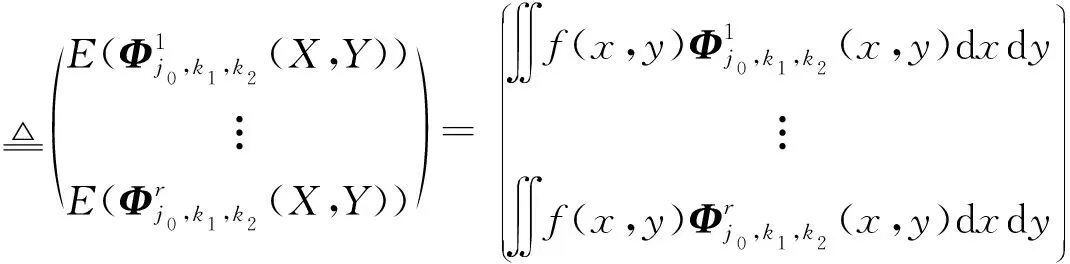
从而得到式(3)的样本估计为

(4)

2 收敛阶证明

其中s为平滑参数，p、m为空间的范数指标，且s>0，1≤p≤∞，1≤m≤∞。

证明：

综上可得

证明：

由1.2节尺度系数估计值可知

由引理2可得

应用Holder不等式可得

综上所述

证明：

其中

由引理1可得

A≤C2-2Js

经计算有

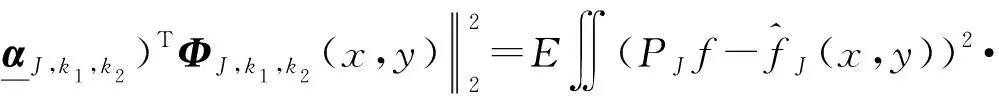
根据引理3可得

又因为2J≤n1/(2s+2)，所以有

3 实验分析

本节通过模拟及实例说明提出方法的可行性，并通过均方根误差值来对比小波密度估计及多小波密度估计的优劣。均方根误差定义为

例1设二元随机变量(X,Y)服从均匀分布，其中x∈[0,1]，y∈[0,1]，密度函数为

本例选取CL2*Db4(*表示乘积)构成的二元多小波以及Db4*Db8构成的二元单小波，对密度函数进行估计，分辨率水平取J=4，样本量n=10 000。

图1为均匀分布的真实的密度函数图像，图2和图3分别为多小波及单小波估计的图像，其中，多小波误差为0.164，单小波误差为0.388。由图1～3可以看出，两种估计均能真实地描述服从均匀分布随机数据的规律，但由于尺度函数的紧支性，当平移向量很大时，图像在边界处渐进有偏，且多小波的偏离程度明显小于单小波。

例2设二元随机变量(X,Y)服从正态分布，其中x∈[0,1]，y∈[0,1]，密度函数为

本例选取STT*Db4和CL2*Db4构成的两个二元多小波以及Db4*Db8构成的二元单小波，对服从正态分布的数据进行仿真实验,分辨率水平J=4，样本量n=10 000。

图4表示真实的正态分布密度函数，图5～7分别为不同基函数的多小波及单小波估计的密度函数图像。从图4～7可以看出，对于边界处为0的正态分布，多小波估计具有较好的估算精度，能够客观地反映出数据的分布规律，且边界处拟合度更佳。由表1和图8可以得出，随样本量的增加，多小波密度估计的误差和运行时间总是小于单小波，且在大样本下优势更加明显。

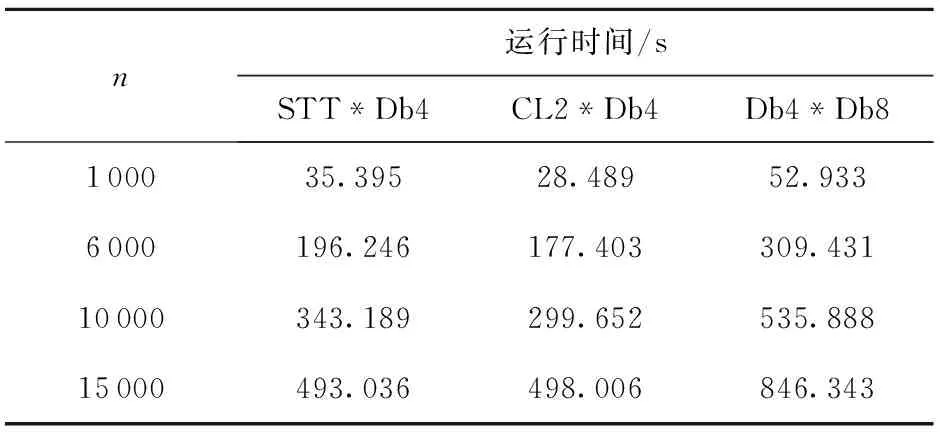
表1 随样本变化估计的运行时间Table 1 Estimated run times of different samples

从线性表达式(式(2)和(4))可以看出，密度函数的信息包含在系数和基函数中，所以估计结果的质量取决于分辨率水平J的选取。表2给出了不同分辨率水平对估计误差值的影响，可以看出，随着分辨率水平J的增加，估计的误差值先变小后变大，且对于不同的基函数，最优分辨率水平不同。

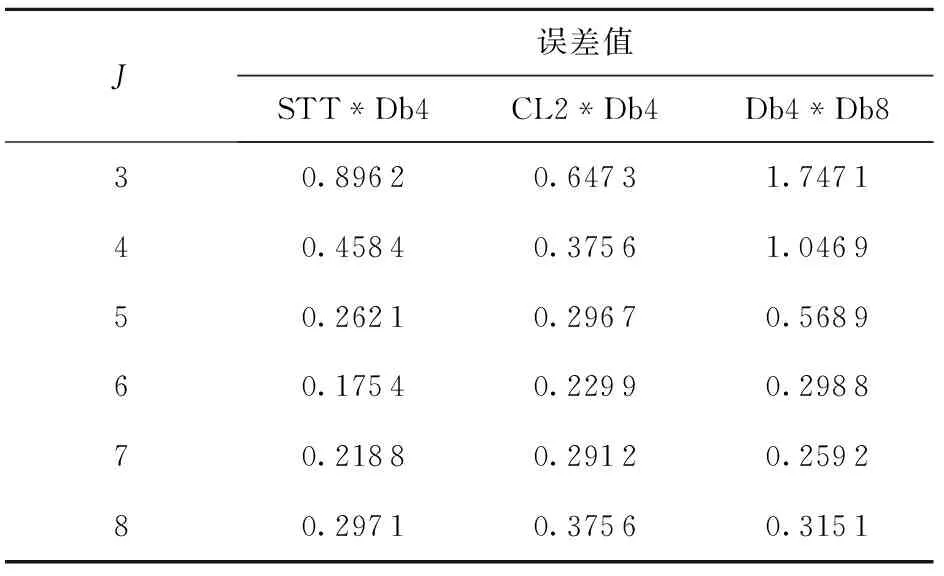
表2 随分辨率水平变化估计的误差值Table 2 Error values of estimates at different resolution

例3实例分析中，二元多小波可以用来估计美国黄石公园中喷泉喷发时长和间隔时长的密度函数，该数据集可在www.geyserstudy.org/geyser.aspx?pGeyserNo=OLDFAITHFU上公开获取。本例选取n=1 922个样本，基函数为CL2*Db4构成的二元多小波，分辨率水平J=3，结果如图9～11所示。

图9和图10分别为喷泉的间隔时长和喷发时长分布直方图，其中横坐标的时长均进行了归一化处理，图11为相应的密度估计图像。本例选取的样本量较少，且数据分布随机性更强，不再服从某一已知的分布函数。从图9～11可以看出，一类二元多小波密度估计图像与喷泉的直方图趋势吻合，能够客观地反映出数据的真实分布规律，说明该方法也适用于更一般的数据分析，在实际应用中是有效的。

4 结论

本文研究了一类二元多小波函数进行概率密度估计的问题，给出了线性多小波估计器，并且证明其在积分均方误差意义下存在收敛上界。在仿真实验中，通过选取不同分布的二元数据进行多小波密度估计，并与单小波进行对比，验证了提出方法能够较好地反映数据的真实分布规律且在某些条件下优于单小波。最后，对实例的数据分析结果表明本文方法在实际应用中是有效的。