基于动态SV模型预测国债利率期限结构

王 睿 周荣喜 李志强

(1.对外经济贸易大学 金融学院， 北京 100029; 2.北京化工大学 数理学院， 北京 100029)

引 言

利率期限结构是用来描述某一时刻不同期限的即期利率与其剩余期限关系及变化规律的函数，它在宏观经济的预测以及债券衍生品的定价和风险管理等方面都有着非常重要的作用[1]，其研究核心在于利率期限结构模型，包括静态模型和动态模型。其中静态模型的操作性、实用性更强[2]，较有代表性的有样条模型和简约模型[3]。1987年Nelson和Siegel[4]提出了第一个简约模型，简称NS模型，之后Svensson[5]在NS模型的基础上提出了SV模型，解决了NS模型不能反映利率曲线多峰的问题，提高了对现实情况中更复杂多样的利率期限结构的拟合能力。NS模型和SV模型因拟合利率期限结构满足光滑性、参数具有较强的经济含义、拟合结果符合利率期限结构预期理论而得到广泛应用，是许多国家中央银行采用的模型。朱世武等[6]采用样条法和SV模型拟合上海证券交易所国债的利率曲线，认为SV模型更加符合中国的实际情况。任姝仪等[7]对NS模型、SV模型等N- S族模型进行实证比较，认为NS模型不能很好描述长期的期限结构形态，SV模型可以拟合利率曲线的双峰和双U形状；实证结果显示，我国利率曲线存在多峰的情况，SV模型的拟合误差小于NS模型，拟合优度大于NS模型，且比NS模型更加稳定。Barrett[8]的研究表明，求解SV模型参数时事先确定λ1和λ2的值，得到的其他参数估计值更加稳健。

相比于利率期限结构的拟合，对利率期限结构预测的研究更具有应用价值。传统的预测主要是对利率曲线本身的时间序列建模，结果显示只在短期内有一定的预测性[9]。Caldeira等[10]运用非参数方法对美国零息债券的收益率曲线进行了预测，结果表明该方法只对期限较短收益率的预测效果较优，期限较长时没有优势。闫红蕾等[11]运用神经网络模型对国债的利率期限结构进行了拟合和预测，但模型的解释力较弱，且对参数依赖性较强。刘晓等[12]运用4种不同的神经网络模型对国债利率期限结构进行了预测，结果显示神经网络的结构、隐层节点数、迭代次数等都对结果有较强的影响，模型的普适性较弱。Diebold等[13]提出了动态NS预测模型，为利率期限结构的预测提供了一种新思路，动态NS模型通过对债券到期收益率水平、斜率和曲率3个因子的预测实现对到期收益率的预测，模型十分简洁，参数具有明确的经济含义；实证研究表明动态NS模型可以充分捕捉利率期限结构的动态变化，且具有较好的预测效果。康书隆[14]运用我国的国债数据证明了基于NS模型参数序列的动态建模方法除具有简洁、可操作性强的优点之外，还能够很好刻画我国利率期限结构的动态变化规律。

结合SV模型的优势以及参数序列动态建模方法的优势，本文基于SV模型构建SV预测模型，通过最小化收益率误差和固定参数将模型求解时的非线性优化问题转化为线性优化问题，增强估计的稳定性，并基于SV模型构建动态SV预测模型，采用中国人民银行的国债即期利率数据进行了实证检验，结果表明预测模型在预测步长较长时的长期利率具有一定的优越性。

1 SV利率期限结构模型与实例验证

1.1 SV模型

Svensson[5]在NS模型的基础上进行了改进，提出了SV模型，其即期利率为

(1)

式中，λ1、λ2、β0、β1、β2和β3为模型的6个参数。之后有学者对这些参数的含义进行了解释[12]：

1)β0被视为水平因子，反映了利率曲线的长期水平，r(∞)=β0，β0>0；

2)β1代表短期利率部分，被视为斜率因子，反映了利率曲线的倾斜程度，|β1|越大，利率曲线越陡峭，β1>0利率曲线为上升形态，β1<0为下降形态；

3)β2和β3分别表示不同的中期利率部分，被视为曲度因子，用来描述利率曲线的峰态，反映了利率曲线的曲度，β2,β3>0时利率曲线为驼峰形态，β2,β3<0时利率曲线为U字形态；

4)λ1和λ2决定β1、β2和β3的收敛速度，也分别决定了β2和β3载荷极值点的位置。

对于式(1)中参数的估计，传统的方法是通过求解最小化债券实际价格与估计价格之差的加权平方和的优化问题得到，但是求解上述的非线性优化问题较为困难，不仅需要找到合理的算法，而且其对参数的初始值有很强的依赖性[15]。Svensson[5]认为这种估计方法可能会导致参数失真，估计不稳定，而最小化收益率误差则相对稳健得多[16]。Koopman等[17]研究发现，模型中的参数λ对利率曲线拟合的误差影响不大，拟合优度也对λ的取值不敏感。因此本文在实证研究中先将λ固定，将非线性优化问题转化为线性优化问题，使用最小二乘估计求得稳定的参数。

1.2 模型参数的估计

首先选取2011年1月至2018年3月每月最后一个交易日，期限为3个月、6个月、1年、3年、5年、7年、10年和30年的即期利率(87×8)面板数据为样本，数据源自中国人民银行网站。对样本数据进行初步统计得出，我国的国债利率期限结构在平均程度上呈现上升形态，短期利率波动大于长期利率，长期利率的自相关程度要大于短期利率，且变化更为缓慢。利用SPSS软件对样本数据进行主成分分析，结果显示前两个主成分对利率曲线的累计解释比例为97.73%，提取的4个主成分对利率曲线的累计解释比例高达99.52%，几乎可以完全解释利率曲线的变动，进一步验证了SV模型用三因素描述利率期限结构的合理性。

鉴于运用传统非线性优化方法求解模型的参数通常不稳定，本文首先设定参数λ1和λ2的值，再通过求解线性优化得到参数β0、β1、β2和β3的值。参数λ1和λ2决定着中期利率部分因子β2和β3的载荷值(1-e-λt)/λt-e-λt在何时达到最大。中国的中期国债发行期限多为1～7年，分别代入(1-e-λt)/λt-e-λt，求出载荷值达到最大时的λ1和λ2对应的取值范围为[0.256,1.793]。

Chronode C502Le Locle的Chronode也生产复杂功能机心，但还提供三种自制机心。创始人Jean-Franois Mojon说： “但我们不是ETA替代厂商：我们的机心是个性化的，每年只生产1千到2千枚机心”公司拥有大约70名员工，有子公司DMP（负责仿形车削）和CHL（负责装饰）。

因此将λ1和λ2的初始范围设定为[0.25,2]，将参数分别按0.01为间隔遍历代入SV模型，按样本数据回归残差最小原则，寻找区间内参数的最优取值，最终得到λ1=0.298，λ2=0.721，此时载荷值(1-e-λt)/λt-e-λt达到最大，对应的期限t大约为6年和2.5年，再将参数λ1和λ2的值代入，得到参数β0、β1、β2和β3的载荷值如图1所示。可以看出β0、β1、β2和β3分别影响着利率曲线的水平、斜率和曲度。在确定了参数λ1和λ2的取值后，对样本区间内每个月的截面数据依次进行最小二乘回归，从而得到参数β0、β1、β2和β3的估计序列以及SV模型拟合的利率期限结构结果。

根据1.1节所述各β的经济含义，本文将β0的理论值假设为30年期国债的即期利率，β1的理论值假设为30年期国债即期利率与3个月国债即期利率之差，β2的理论值假设为5年期国债即期利率的2倍与3个月期国债即期利率及30年期国债即期利率之和的差，β3的理论值假设为3年期国债即期利率的2倍与3个月期国债即期利率及30年期国债即期利率之和的差。各β估计值的统计量见表1，估计结果及与理论值的对比如图2所示。

表1 β估计值的描述性统计量Table 1 Descriptive statistics of β estimates

计算各β参数估计值与理论值的相关系数，得到β0估计值与理论值的相关系数为0.980，β1的相应值为0.974，β2的相应值为0.850，β3的相应值为0.702。从图2和表1的结果也可以看出，估计值与理论值高度一致，估计标准差基本稳定在一定范围内，模型参数估计整体较为准确稳健。

1.3 拟合结果与分析

通过估计得到模型参数后，将样本数据代入式(1)得SV模型，最终得到的拟合结果及残差如表2和图3～5所示。

表2和图5的残差结果说明，SV模型基本上可以准确描述出利率期限结构的变动趋势，残差的绝对值和波动也较小，模型整体的拟合效果较好。相较而言，中期利率的拟合误差和波动更大一些。

表2 样本区间拟合残差描述性统计量Table 2 Descriptive statistics of fitting residuals in sample interval

2 基于动态SV模型的利率期限结构预测

2.1 β的平稳性与相关性检验

首先对得到的参数β估计序列进行检验分析，然后根据其自身的特征建立时间序列模型，最后进行样本外预测，检验模型的预测效果。对β0、β1、β2和β3的估计序列进行单位根检验，结果显示β0和β1可能存在单位根，一阶差分平稳，β2和β3满足平稳性。

各个参数β的相关性检验结果如表3、4所示，可以看出，各参数之间都存在一定的相关性。其中β0的自相关性最强，β1和β2之间的相关性最强。但与Diebold等[13]使用美国国债数据计算出的结果相比，本文中参数β的自相关性相对较弱。

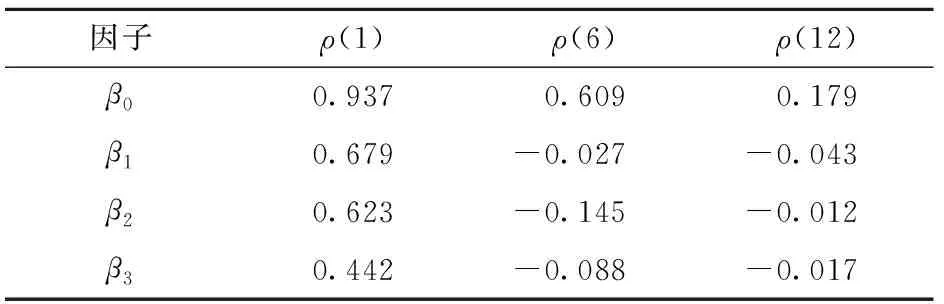
表3 参数β的自相关系数Table 3 Autocorrelation coefficient of parameter β

2.2 动态SV模型的构建

根据所得参数β的性质与经济含义，决定利用AR(1)模型和VAR(1)模型对参数β进行预测。为了更直观地检验动态SV模型的预测效果，引入随机游走预测模型与其进行比较。具体的动态SV模型构建如下。

表4 各参数之间的相关系数Table 4 Correlation coefficients between parameters

1)SV- AR(1)模型

(2)

i,t+h=i+ii,t，i=2,3

(3)

2)SV- VAR(1)模型

(4)

t+h=+t

(5)

3)随机游走预测模型

t+h(τ)=rt(τ)

(6)

2.3 模型预测的实证检验

首先将样本区间分为两部分，其中，2011年1月至2015年12月为样本内区间，共60个月，2016年1月至2018年3月为样本外区间，共27个月。预测步长分别设置为1个月、6个月和1年，得到的结果如表5～7所示，表中的均值、标准差及均方根误差是对各期限的预测收益率与理论值误差的统计。

表5 样本外预测步长为1个月的利率预测结果Table 5 Out-of-sample forecast results for a 1-month

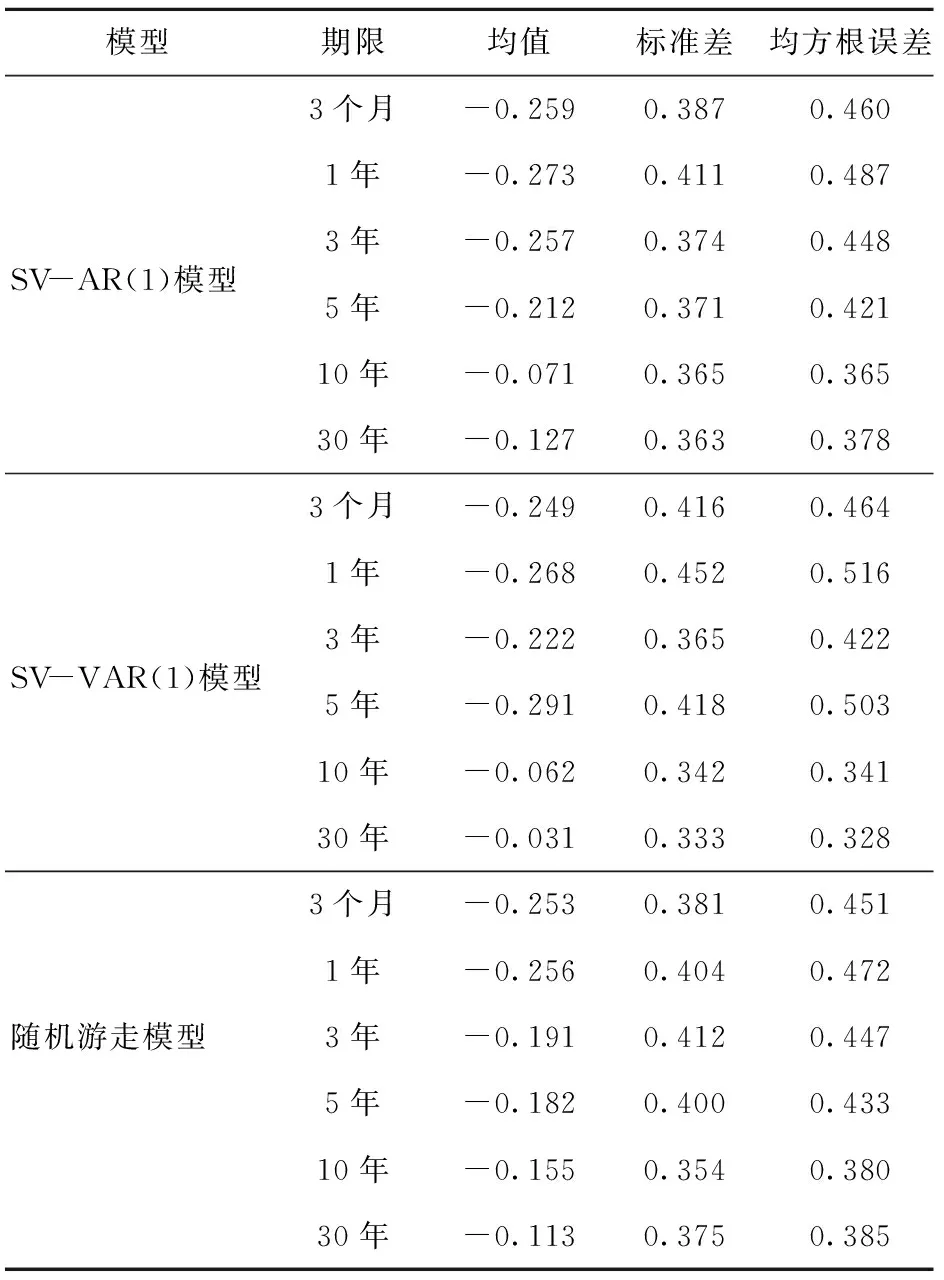
表6 样本外预测步长为6个月的利率预测结果Table 6 Out-of-sample forecast results for six months

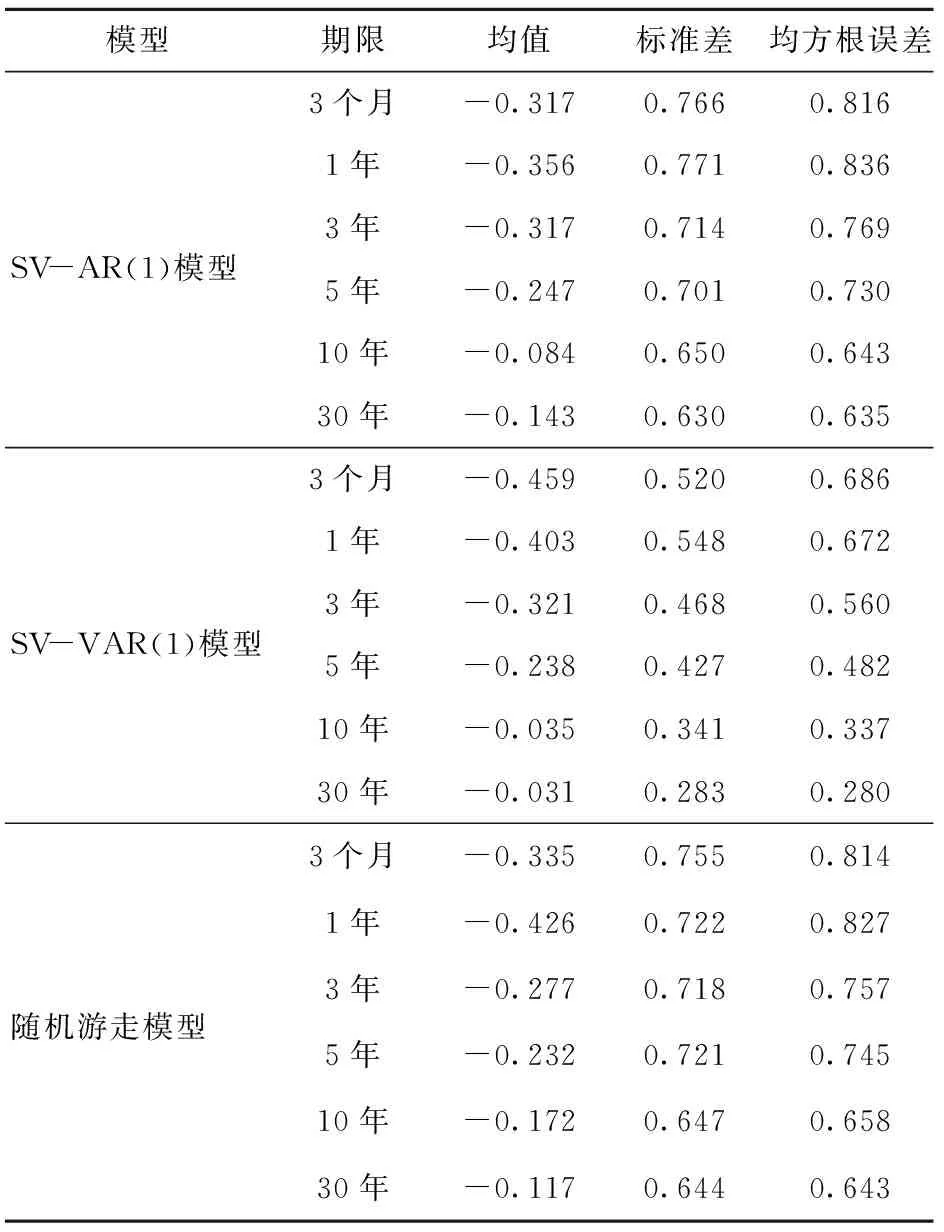
表7 样本外预测步长为1年的利率预测结果Table 7 Out-of-sample forecast results for 1-year

从各模型的预测结果来看，预测步长为1个月时，SV- AR(1)模型和随机游走模型预测误差的标准差和均方根误差基本相同，但随机游走模型预测误差均值的绝对值相对更小，SV- VAR(1)模型的预测效果不甚理想，相比前两者误差较大。总体来看，两种动态SV模型的预测效果并没有优于随机游走模型。

预测步长为6个月时，3种模型对中短期利率的预测效果差别不大，相比而言，随机游走模型效果更好一些，但对于长期利率，SV- VAR(1)模型表现较好。

预测步长为1年时，SV- AR(1)模型和随机游走模型的预测效果基本一致，但SV- VAR(1)模型表现出较强的优势，特别是对中长期利率的预测，预测误差均值明显小于另外两个模型，且所有期限预测的误差标准差和均方根误差均显著降低，预测的稳定性较大。

综上可以得出，预测步长较短时，动态SV模型没有表现出明显的优势，但随着预测步长的增加，动态SV模型逐步显示出一定的优势，特别是对于长期利率的预测，当预测步长为1年时，SV- VAR(1)模型显示出比较明显的优越性，误差的均值和标准差大大减小。对于两种动态的SV模型，预测步长较短时，SV- AR(1)模型相对更好，但当预测步长增加时，SV- VAR(1)模型开始显示出自身的优势。因此可以得出，动态SV模型总体上更适合预测步长较长时的长期利率，相较而言，SV- VAR(1)模型的表现更好。

3 结论

(1)基于SV模型的思路，通过转化参数求解的非线性优化为线性优化问题得到更为稳定的参数估计值，样本拟合实证结果较好，参数β0的估计序列与理论值序列的相关系数为0.980，β1为0.974，β2为0.850，β3为0.702。

(2)基于通过预测模型参数β来实现利率预测的思路，构建了 SV- AR(1)预测模型和SV- VAR(1)预测模型，将预测步长设置为1个月、6个月和1年，对动态SV模型进行了样本外实证检验，结果显示，预测步长为1个月时，SV- AR(1)模型和随机游走模型预测误差的标准差和均方根误差基本相同，两种动态SV模型的预测效果相较于随机游走模型无明显优势；预测步长为6个月时，3种模型对中短期利率的预测效果差别不大，但对于长期利率，SV- VAR(1)模型的预测误差均值明显小于其他两种模型；预测步长为1年时，SV- AR(1)模型和随机游走模型的预测效果基本一致，而SV- VAR(1)模型表现出较强的优势，预测误差的均值、标准差以及均方根误差均明显小于其他两个模型。