叠合板架立筋整体变形及受力计算分析

姜魏

（中国建筑第二工程局有限公司）

1 装配式建筑中叠合板相关构件概述

叠合板融合了现浇板和预制板的所有优势，并且比较薄的叠合板预制部分还可以在工厂中完成，在吊装完成之后可以在叠合板的上端部分实施现浇施工，预制部分可以当做是永久性的模板来实现荷载能力。

叠合板的预制部分板材比较薄，弯矩荷载的压力主要是依靠混凝土自身、埋设在混凝土薄板中的桁架筋以及构造配筋三部分共同承受的。但是为了保障叠合板在一些施工过程中，如吊装中的抗裂和变形性能，对混凝土自身、埋设在混凝土薄板中的桁架筋以及构造配筋三部分的荷载分担能力和各个变形情况进行分析是非常重要的，在这个分析过程中需要根据这三个部分的协调性和变形性能为基础进行对比，并在相关的规范和要求情况下进行控制，可以对叠合板整个的构件的抗弯性分析提供重要的保障[1]。

在我国建筑行业的发展中，装配式建筑开始慢慢的发展起来，很多城市的高端住宅项目，装配式建筑以其成本低、节能环保等特点被广泛的应用，装配式建筑涉及的预制构件主要包括了预制楼梯、预制外墙、钢筋桁架混凝土叠合板、预制阳台等多种预制构件，其中叠合板是在工厂中先对楼板的底部钢筋桁架进行浇筑预制，在混凝土的强度达到所需要的标准之后，再运送到施工现场进行装配。在叠合板的应用中，叠合板架立筋会受到相应的压力出现变形。因此，应针对装配式建筑中，叠合板架立筋整体变形和受力的情况进行分析和和计算。

2 叠合板架立筋整体变形以及受力计算

2.1 弹力学计算分析

混凝土和钢筋构件对缝隙的控制需要根据二级裂缝控制来计算，也就是在现有的荷载能力下对各个构件的受拉边缘的应力要低于混凝土的受拉力值的设计[2]。

针对C30混凝土的受拉力设计值所对应的应变参数是ε0=fkt/Es= 6.8× 1 0-5，如果按照相关的平面架设，桁架筋的下弦杆和构造筋应该是ε下=ε0/6 =1.11*10-5。此外，在一个固定宽度的叠合板相应的受拉钢筋，其中包括了构造配筋和桁架筋中的下弦钢筋等所承受的拉力为 ：ε下=AsEs=1.2kN。另 外 构 造 筋的受力是0.75kN，桁架筋的下弦杆的受力是0.5kN，构造筋所承受的弯矩是Msg=0.01875KN·m。桁架筋所能承受的弯矩为Msh=0.036 KN·m，叠合板可以承受的拉力和曲应力最高值应该是ε0Ec=2.01N/mm2，通常在固定宽度内的叠合板混凝土所需要承受的弯矩是Mc=1.205 KN·m。这样，叠合板立筋架整体的变形力是Mt=Msg+Msh+Mc=1.261 KN·m。叠合板桁架筋的变形压力的承受能力是0.036/1.261=2.89%[3]。

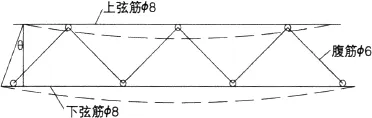
图1 桁架筋和腹筋变形情况

2.2 桁架立筋整体变形的计算

在叠合板的整体桁架变形压力下，一般下弦杆是2根φ8mm的钢筋，上弦杆是1根φ8mm的钢筋，但是在两者的变形压力和变形的协调性中，上弦杆钢筋的变形压力是下弦杆钢筋拉伸变形压力的2倍(见图1)。根据弹性力学的相关理论来说，下弦筋的应变值是ε下=1.12×10-5的情况下，上弦钢筋的应变值应该是ε上=2ε下=2.24×10-5。纵向的桁架筋，一个单位长度中的上弦和下弦的变形趋势如下图1所示，但是按照对应单位长度计算的话，上弦筋的压缩力是△上=ε上1=2.24×10-5m，而下弦筋的变形量是△下=ε下1=1.12×10-5m。

另外上弦筋在下弦筋以及腹筋相互作用的影响下也会出现压缩变形（见图2）。而腹筋主要是由转角Φ形成的顺时针转动，如果转动是LΦ，这样在出现变形的时候就会导致上弦筋压缩变形压力达到（72/123.2）LΦ，并且上弦筋转动时的变形压力是（100/123.2）LΦ。由Φ和θ两者的关系还可以计算出上弦筋的变形压力是△上=6.71×10-6m。由此可以得出两个相近的下弦筋三角会因为转角而出现的上弦筋变形，并且变形压力是6.71×10-6N，这个数值是上弦筋绝对值的变形，大概为200mm，如果换算成长度单位下上弦筋的变形压力是3.3624×10-5N。

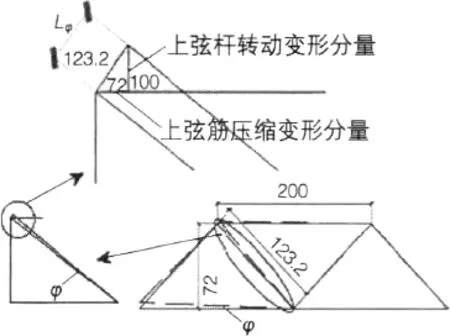
图2 架立筋及腹筋协调变形计算是示意图

如果按照上弦杆的压缩变形来对桁架筋叠合板的弯矩的压力来算的话，在一个单位宽度的桁架筋所需要承受的弯矩应该是Msh=0.0608KN·m，而构造筋所承受的弯矩则是 Msg=0.01875 KN·m，每个单位宽度内的叠合板混凝土的承受弯矩是 Mc=1.206 KN·m，这 样 就 可 以推断出叠合板架立筋整体的弯矩抗力应该 是Mt=Msh+Msg+Mc=1.286 KN·m。 桁架筋对整体变形压力所作出的抵抗力是0.0608/1.206=5.0%。

2.3 架立筋的有限元桁架模型计算

桁架筋的上弦筋和下弦筋采用单元模型计算，通过按照实际的桁架筋的截面情况来设计模型桁架筋的截面面积。另外在腹筋方面，主要是采取的桁架二力杆单元的模型，这样腹筋在模型中就可以承受住轴力的作用，并且不再受到剪力和弯矩的影响。如果桁架筋的跨度是2.4m，在模型的两端一般需要使用铰支来进行固定，之后再在下弦筋和腹筋相连接的地方来设置集中的使用力，这样节点竖方向的受力就能达到1kN。在这样的情况下，各个跨腹筋和下弦筋相连接的地方就会出现一定的弯矩力。此外，叠合板的架立筋会受到上弦筋、下弦筋以及腹筋的轴力，压力出现一定的变形情况。其中在跨中的地方变形会比较大，最大位置受力为7.2 KN·m的地方，下弦筋也会受到一定的拉力，这个拉力为1.63kN，而上弦筋受到的压力为99.97kN，并且上弦筋的设计一般强度是270N/mm2，其的应轴力就达到了13.5 KN·m，相比较上弦筋的压杆稳定设计的值是可以实现计算的[4]。

另外，按照梁单元的计算方式来看（见图3），上弦筋的弯矩是比较小的，相对应的幅值是6.67 KN·m，这个数值是可以忽略不计的。此外上弦筋还可以按照轴心的压杆来计算，两腹筋和上弦筋的交叉点的位置之间的间距达到了200mm，这样就可以计算出上弦筋可以承受的压力的稳定值情况。上弦筋的计算长度是200mm，转动的惯量是πd4/64=200.96mm4，回转半径为：其中构件的长细比是λ=1/i=200/2=100，实腹式受压构件的稳定性是

图3 上弦和下弦筋弯矩示意图

式中，N代表的是压杆稳定设计值；φ代表的是轴心受压稳定系数。根据这时候φ是0.585。压杆保持稳定的设计值是7.9KN。

在以三维桁架筋为基础的模型中，一般按照13mm的板厚，600mm的桁架筋之间的间距，1.6m支撑的间距来进行设计的模型受力计算。一般按照A类型的桁架筋进行计算的话，上弦筋和下弦筋φ8mm和腹筋φ6mm，支撑间距是1.6m，梁支撑一般按照铰接连接计算，模型的节点荷载能力以1kN计算，桁架各个梁以及杆单元的轴力会各有不同。但是按照相关规定的计算方法的弹力学理论计算的话，如果叠合板按照一定的抗裂进行验算的时候，下弦筋的应变控制值为ε下=1.12×10-5，变形的控制拉力是0.112 KN。在计算单位内力作用的时候，单根的下弦筋受力大概是7.04 KN，相应的桁架筋所需要承受的控制变形压力。如果在0.112kN的荷载压力下，相对应的桁架筋下弦筋的跨中最大的弯矩为0.054 KN·m，上弦筋受力应该0.706 KN，压杆保持稳定的压力值为7.9 KN。

在这样的背景下，按照叠合板的抗裂情况进行验算的话，一个单位宽度的桁架筋有限的三维模型的跨中最大的压力可以达到Msh=0.051×3/1.2=0.1275kN·m；叠合板的混凝土所能承受的弯矩值是Mc=1.206 KN·m；构造筋可以承受的弯矩值是Msg=0.01875kN·m。由此可以计算出叠合板整体的变形压力为Mt=Msg+Msh+Mc=1.352kN·m。其中桁架筋对整体的抗弯度的贡献值是0.1275/1.352=9.4%。