基于4-叉树结构的路网数据最近邻查询算法
2020-10-10陈可心陈业斌
陈可心,陈业斌
(安徽工业大学计算机科学与技术学院,安徽马鞍山243032)
路网数据由于其结构的复杂性和庞大的数据量,使用一般的查询算法很难满足其对兴趣点(point of interest,POI)查询效率的需求[1-3]。如何利用新的查询算法或改进现有的查询算法来提高查询效率是一个值得研究的问题。鲍金玲等[4]综述了路网环境下的最近邻查询技术,对2018年之前应用在路网领域中的查询算法进行了比较分析;陈业斌等[5]提出基于Spark SQL(structured query language)的查询方法,在Spark 中嵌入索引管理机制,将其封装在弹性分布式数据集内,用于提高查询效率;于启迪等[6]通过对线性树型结构的改进,提出一种基于自适应虚拟树存储结构、利用空间关键词查询来提高查询效率的查询算法;Bok等[7]、Chan等[8]提出利用不同单元格点距离的排序构建索引表,以此提高k近邻查询的效率;陈小迪等[9]对基于路网k近邻查询的相关算法进行了比较,并展望k近邻查询算法未来的研究方向和重点;闫红松等[10]利用分治法的思想,将查询区域进行网格划分,缩小有效的查询区域,快速定位查询点所在路径,进而找到最近邻数据点;朱良等[11]提出了k聚集最近邻数据查询方法。现有文献多聚焦于查询算法本身的效率改进,较少关注数据本身的存取问题。鉴于此,文中提出一个新的思想:利用Voronoi图对空间进行划分,确定兴趣点的位置,利用空间分区技术将空间划分至理想大小,利用4-叉树结构存储兴趣点,并建立相应的索引表,最后结合最近邻查询算法找出最近的兴趣点。
1 空间数据最近邻查询相关技术
最近邻(the nearest neighbor,NN)查询为空间数据查询中应用比较普通的一种查询技术,其查询思想可描述为:给定网络数据集K和查询点q,在网络数据集K中查询q距离最接近的点p(p∈K),若找到返回点p,则点p为数据集K中与查询点q的最近邻点。路网空间数据集K中,通常称查询的目标点p为兴趣点(POI),这种兴趣点通常不止一个,以|q,pi|表示q和pi两点之间的距离,q的最近邻点p用NN(K)表示,如式(1)

Voronoi图是由一组连接两点的垂直平分线构成的连续多边形组成,又称泰森多边形。假设欧氏空间的点集P={p1,p2,…,pn},Voronoi图以点集P中的每一点作为生成元来划分平面区域,如式(2)

其中:V(pi)为划分出的平面区域;d(p,pi)表示点p 到点pi的距离。Voronoi 图具有按距离划分临近区域的特征,使用Voronoi图可将空间数据集划分为n个空间单元,使用不同标识(identification,id)号标识不同的单元,并将单元中兴趣点的相关信息存储到相应数据结构中,数据结构中至少包含id(即空间单元id)、内容和位置坐标等信息。给定任意查询源点q,若查询q点的最近邻点(目标点),需遍历所有POI。
2 路网空间结构化分区与信息存储
在欧氏空间中,若查询最近邻,则需遍历所有的POI,查询效率不高。文中以路网数据及其结构为研究对象,首先对其空间结构进行均分,用树型结构存储查询信息,对查询区域进行准确定位,以降低查询的目标范围,提高查询效率。空间均分法(part half cut method,PHC)的思路为:在欧氏空间的基础上,将整块空间均分为B1,B2,B3,B44个区域,再使用相同方式对每个区域进行第二次划分,两次划分后将产生42个区域,第三次划分后将产生43个区域,循环迭代出4n个区域,直到每个分区中POI的密度满足某个给定的值为止,空间均分法示意图如图1。
使用空间均分法划分空间的过程中,空间区域是以4 的指倍增加,新产生块的信息可使用4-叉树结构保存。根节点指向树中第0 层节点,当整个空间被第一次切分后会产生B1,B2,B3,B44 个节点,此为第1 层节点;第二次切分会得到16 个节点,依次为B12,B13,B14,…,B41,B42,B43,B44,此为第2 层节点。通过循环迭代直到最后分区中的查询点数量满足区域分割粒度要求为止,迭代完成后构造出4-叉树结构,如图2。

图1 空间均分法示意图Fig.1 Schematic diagram for part half cut method
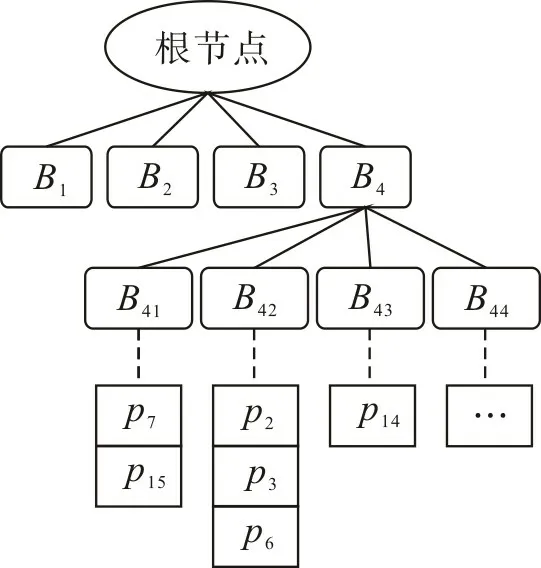
图2 4-叉树存储结构示意图Fig.2 Schematic diagram for quad-tree storage structure
4-叉树结构的叶子节点即为最后的分区块,通过计算可得每块的坐标信息,Voronoi 图中每个POI的数据结构中存储有位置坐标。在构建4-叉树结构过程中,若POI中的点坐标被块坐标包含,则将该POI存储到该叶块的数据链表中,如表1。这样就可将查询范围直接定位到某区块下的数据链表中,大大缩小查询范围,提高查询效率。

表1 分区索引表Tab.1 Partitioned index table
3 基于4-叉树结构的最近邻查询算法流程
要查询q点的最近邻点,q点即为查询源点。输入q点坐标及查询内容,根据q点坐标找到其所在的叶子节点,即q点位于的最小分区块,通过和叶子节点中存储的信息链表对比查询兴趣点。若找不到目标,则通过在该叶子节点相邻的叶子节点链表中迭代查询;若相邻的叶子节点中仍找不到,则转到其父节点相邻节点的叶子节点数据链表中迭代查找。找到的目标节点即为最近的POI,即最近邻,其算法流程如图3。
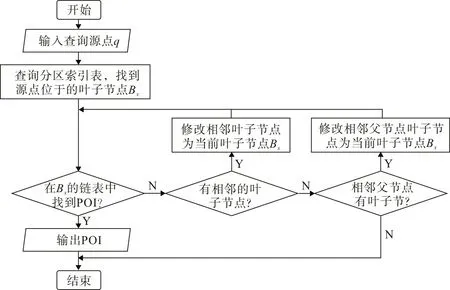
图3 最近邻查询算法流程图Fig.3 Algorithm flowchart of the nearest neighbor query
4 实验结果及分析
4.1 实验
对于路网数据分区查询,传统的划分方法有兴趣点迭代切分法(iterative division between points method,IBP)和折半分割法(half split method,HM)[12]。其中:IBP是基于POI的密度进行分区;HM是基于空间中POI 的数量进行均分。为验证本文提出的均匀划分(PHC)最近邻查询算法的有效性,文中采用PHC,IBP和HM 3种方法对路网数据进行分区查询实验,基于分区中兴趣点数量对分区时间和查询时间的影响,比较分析PHC,IBP和HM 3种方法的分区性能。
实验测试设备为实验室中的PC 机,操作系统为64 位的WIN10,使用型号为7-4510U 的CPU,主频为2.6 GHz,内存为8 GB。使用Eclipse开发平台和Java语言实现最近邻查询算法。实验数据取自开源wiki地图(open street map,OSM)官网的路网数据,数据大小为16 GB,数据格式为XML格式,将其转换为TXT格式的目标文件,目标文件有两个:block.txt和node.txt,格式数据按行存储。block文件中数据结构为{B_id,x1,y1,x2,y2,Bf_id,Bc_id,Bb_id},其中:B_id为分区块的唯一标识;x1,y1,x2,y2为块坐标;Bf_id为父块标识;Bc_id为子块标识;Bb_id为相邻块标识。node文件中数据结构为{B_id,N_id,x,y,content},其中:B_id为分区块的唯一标识;N_id为当前POI的id;x,y为POI坐标;content为POI内容。

图4 分区时间与POI数量的关系Fig.4 Relationship for partition time and number of POI
4.2 实验结果与分析
4.2.1 兴趣点数量对分区时间的影响
为能较好地显示分区数量一定的情况下,POI数量对分区时间的影响,选取POI 数量(|D|)变化区间为200~2 000 个点,空间均分法(PHC)、基于兴趣点迭代切分法(IBP)、折半分割法(HM)3种方法的分区结果如图4。由图4可看出:POI数量为1 000时,PHC,HM,IBP的消耗时间分别为0.12,0.18,0.38 s;POI 数量为1 500 时,PHC,HM,IBP 的消耗时间分别0.35,0.59,1.18 s。由此表明,PHC,HM,IBP 3 种分区方法的消耗时间随着兴趣点数量的增加均呈线性分布,其中IBP消耗时间的增长速度比HM更快,PHC消耗时间增长最慢,效果最好。
4.2.2 兴趣点数量对查询时间的影响
在POI 数量一定的情况下,PHC,IBP,HM 3 种方法最近邻查询时间与分区数量的关系如图5。由图5可看出:分区数量为400时,PHC,HM,IBP的消耗时间分别为0.42,0.82,0.88 s;分区数量为600时,PHC,HM,IBP 的消耗时间分别0.24,0.80 0.86 s。由此表明:在POI 数量一定的情况下,当分区数量k增加时,每个分区中需查询的POI数量减少,3种方法的查询耗时都会降低;但空间均分法(PHC)通过分区方式产生最佳平衡的分区元素,效率最高。

图5 查询时间与分区数量关系Fig.5 Relationship for query time and number of partitions
5 结 论
针对路网数据中数据量较大、查询效率低等问题,提出利用4-叉树结构对路网数据进行均匀划分的最近邻查询算法。实验结果表明,与基于兴趣点迭代切分法(IBP)、折半分割法(HM)相比,基于4-叉树结构的路网数据最近邻查询算法具有更高的查询效率,可减少查询所要访问的POI数量,降低查询开销。但本实验查询对比的内容相对简单,如何基于中文字符进行复杂内容比较是下一步研究的问题。
