大型三排滚柱式回转支承的摩擦力矩特性研究
2020-10-10冯建有许丽华
冯建有,许丽华,侯 宁
(1.安徽工业大学机械工程学院,安徽马鞍山243032;2.马鞍山统力回转支承有限公司,安徽马鞍山243000)
回转支承是盾构机、起重机及挖掘机等重型机械中重要的传力元件之一,其运行及受力的主要特点是低速、重载[1-4]。此外,回转支承广泛应用于可再生能源行业,如风力发电机的偏航和俯仰旋转系统等。作为重型旋转机械传力元件的重要组成部分,降低回转支承功耗十分重要,而回转支承摩擦力矩是产生其功耗的主要根源[5]。因此,回转支承的设计、制造及应用过程中摩擦力矩是需要关注的重要参数之一[6-7]。
国内外学者对回转支承的摩擦力矩计算进行了许多研究,如徐立民等[8]、冯培恩[9]、何西冷[10]运用叠加法分析了回转支承的当量载荷,并利用近似计算公式研究了摩擦力矩与外载荷的关系;李秀珍等[11]实验研究了某型号风电机组变桨轴承的摩擦力矩,讨论了倾覆力矩、转速对摩擦力矩的影响;王燕霜等[12]利用拟静力学方法建立了四点接触变桨轴承的平衡方程,分析了负游隙对四点接触变桨轴承摩擦力矩的影响;张占立等[13]通过理论计算和实验测量分析了负间隙工况下四点接触转盘轴承的摩擦力矩特性,拟合了负游隙与启动摩擦力矩的计算公式;陆静等[14]利用钢球与滚道间摩擦力矩的方法,研究了四点接触球转盘轴承几何参数(如接触角、沟曲率半径系数、钢球直径等)对摩擦力矩的影响;Κania等[15]以双排球回转支承为研究对象,建立了接触区域钢球-滚道模型,重点讨论了径向载荷对摩擦力矩的影响;Heras 等[6-7]对四点接触回转支承的摩擦力矩特性进行了研究,分析了现有摩擦力矩计算模型的适用性和局限性,讨论了制造误差、套圈刚度对摩擦力矩的影响;在此基础上Heras等[16]进一步研究了考虑制造误差和套圈柔性的四点接触回转支承的载荷分布和摩擦力矩特性。从上述文献可以看出,国内外学者对于大型滚柱式回转支承的研究多集中于滚道压力分布、承载能力及寿命等方面的理论计算和有限元分析[17-24],对于滚柱式回转支承摩擦力矩特性的探讨较少,缺少对滚柱式回转支承摩擦力矩影响因素的研究。鉴于此,文中以三排滚柱回转支承为对象,建立滚柱与滚道之间接触压力分布的理论计算模型,给出三排滚柱回转支承摩擦力矩计算公式;且以某型号三排滚柱回转支承为例,分析外部载荷和结构参数对其摩擦力矩的影响,以期为低摩擦力矩三排滚柱式回转支承的设计提供一定参考。
1 回转支承静力学计算模型
1.1 几何模型
三排滚柱式回转支承的几何结构如图1。其中上下两排滚柱为轴向滚柱,中间一排滚柱为径向滚柱。轴向载荷和倾覆力矩由上下两排水平滚柱承受,径向力则由垂直布置的滚柱承受。文中三排滚柱式回转支承主要参数如表1。

图1 三排滚柱式回转支承Fig.1 Three-row roller slewing bearings

表1 三排滚柱式回转支承参数Tab.1 Three-row roller slewing bearing parameters
为分析三排滚柱式回转支承滚柱与滚道之间的接触压力分布,建立如图1(b)所示坐标系。z轴沿回转支承转轴方向,回转支承中每两个滚柱之间间隔为2πp/zi(i=1,2,3, 分别表示上排柱滚道、下排柱滚道及径向滚道),每个滚柱的位置角可表示为φij=2π(j-1)/zi(j=1~zj),其中zj为滚柱数目。文中以δa,δr及θ 分别表示回转支承受外载荷后产生的轴向位移、径向位移和倾角。对回转支承进行受力分析时,为便于计算采取如下假设:只考虑滚柱与滚道接触处的弹性变形,忽略内外圈的变形;各排滚柱的直径及长度均匀;由于转速较低,故可按照静力学模型来处理;外圈固定内圈转动,载荷作用于内圈上。
三排滚柱式回转支承的横截面如图1(a),在外载荷作用下,滚柱和滚道之间形成3个接触对,为叙述方便将其命名为接触对1、接触对2和接触对3。回转支承受载之前、对零间隙回转支承、三排滚道上任意滚柱位置接触对的滚道间距分别为:

若回转支承的轴向间隙和径向间隙分别为ua和ur,则回转支承受载之前三排滚道上任意滚柱位置接触对的滚道间距为:

回转支承承受载荷之后内圈产生位移,每个滚柱位置接触对的滚道间距均会发生变化,由图1中几何关系,在任意位置角处接触对1,2,3的间距A1φ,A2φ和A3φ分别为:

在任意位置角φ 的接触对处,滚柱与滚道总的弹性接触变形量为

根据Hertz接触理论,接触对i在位置角f 处,滚柱与滚道的法向接触载荷Qiφ和接触变形δiφ的关系如下[25]:

式中K 为滚柱与两个接触滚道总的负荷变形常数,其计算方法如下[25]

式中:μ1,μ2分别为滚柱和滚圈材料的泊松比;E1,E2分别为滚柱和滚圈材料的弹性模量;L为滚柱长度。
1.2 力学模型
回转支承在外载荷作用下处于平衡状态,以内圈为研究对象,其平衡方程为:

式(9)~(11)构成的方程组是以三排滚柱式回转支承的内圈位移量δa,δr及θ 为未知量构成的三元非线性方程组,可采用离散牛顿迭代法进行求解,得到δa,δr及θ,再根据式(7)即可求得三排滚柱式回转支承中每个滚柱与滚道之间的接触压力。
2 回转支承摩擦力矩的计算
滚柱式回转支承摩擦力矩是由各种摩擦因素对其旋转构成的阻力矩,精确计算其摩擦力矩是一个复杂的问题,其不仅与回转支承自身的结构尺寸、材料性能、硬度、间隙、加工制造的尺寸误差有关,还与工作载荷、环境温度、润滑条件等因素有关。对于低速重载工况下的回转支承,其摩擦产生的主要因素有滚柱与滚道接触变形区域内的弹性滞后、微滑动、滚柱与座圈及隔离块间的滑动摩擦。根据回转支承的受力特点,可将其摩擦力矩分成两步进行计算:由倾覆力矩和轴向载荷引起的上下排滚柱与滚道之间的摩擦力矩;由径向载荷引起的径向滚柱与滚道之间的摩擦力矩。
2.1 由轴向载荷和倾覆力矩引起的摩擦力矩

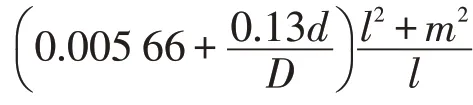
2.2 由径向载荷引起的摩擦力矩

式中:M2为纯径向载荷引起的摩擦力矩;μ3为径向载荷Fr在滚柱与滚道间的当量摩擦系数,取0.002[8]。
综上,三排柱式回转支承总摩擦阻力矩为

3 回转支承摩擦力矩特性分析
文中以型号为131.32.2000.00Z的三排滚柱式回转支承为例,在利用静力计算模型得出滚道压力分布的基础上,利用摩擦力矩计算公式分析载荷参数和结构参数对摩擦力矩的影响。三排滚柱式回转支承的主要参数如表1。
3.1 载荷参数对摩擦力矩的影响
图2为纯轴向力工况和纯倾覆力矩工况下,摩擦力矩随当量轴向载荷的变化关系。图中倾覆力矩斜直线表示的是纯倾覆力矩工况下,倾覆力矩与当量轴向载荷之间的关系。由图2 可知,摩擦力矩随当量轴向载荷的增大呈线性增大的趋势;在相同当量轴向载荷情况下,轴向力引起的摩擦力矩明显大于倾覆力矩引起的摩擦力矩。
3.2 结构参数对摩擦力矩的影响
3.2.1 间隙对摩擦力矩的影响
图3 为回转支承外载荷及其他参数不变时,间隙对摩擦力矩的影响。由图3 可知:当间隙在0~0.4 mm 范围逐渐增大时,摩擦力矩逐渐减小,但变化幅度很小,即正间隙对回转支承的摩擦力矩影响很小;当间隙在-0.4~0 mm范围增大时,摩擦力矩迅速减小,即负间隙对回转支承的摩擦力矩影响很大,主要原因是滚柱与滚道之间的接触压力发生了变化。图4 为不同间隙情况下,滚柱与滚道接触压力的分布曲线。由图4 可知,随着回转支承正间隙增大,有效承载的滚柱数目逐渐减少,滚柱与滚道的最大接触压力随之增大,但此时回转支承的当量轴向载荷几乎不变,故摩擦力矩没有明显变化;当回转支承负间隙绝对值增大时,承载滚柱数目随之增多直到所有的滚柱均承受载荷,但由于负间隙的存在,滚柱与滚道之间的接触变形增大,导致回转支承的当量轴向载荷随负间隙绝对值的增大而增大,造成摩擦力矩随负间隙绝对值的增大而迅速增大。
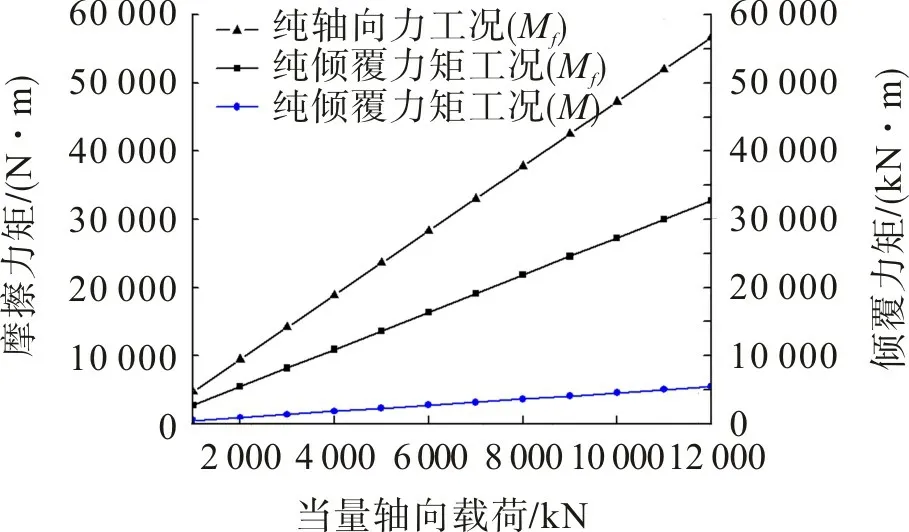
图2 外载荷对摩擦力矩的影响Fig.2 Influence of external load on friction torque

图3 间隙对摩擦力矩的影响Fig.3 Influence of clearance on friction torque
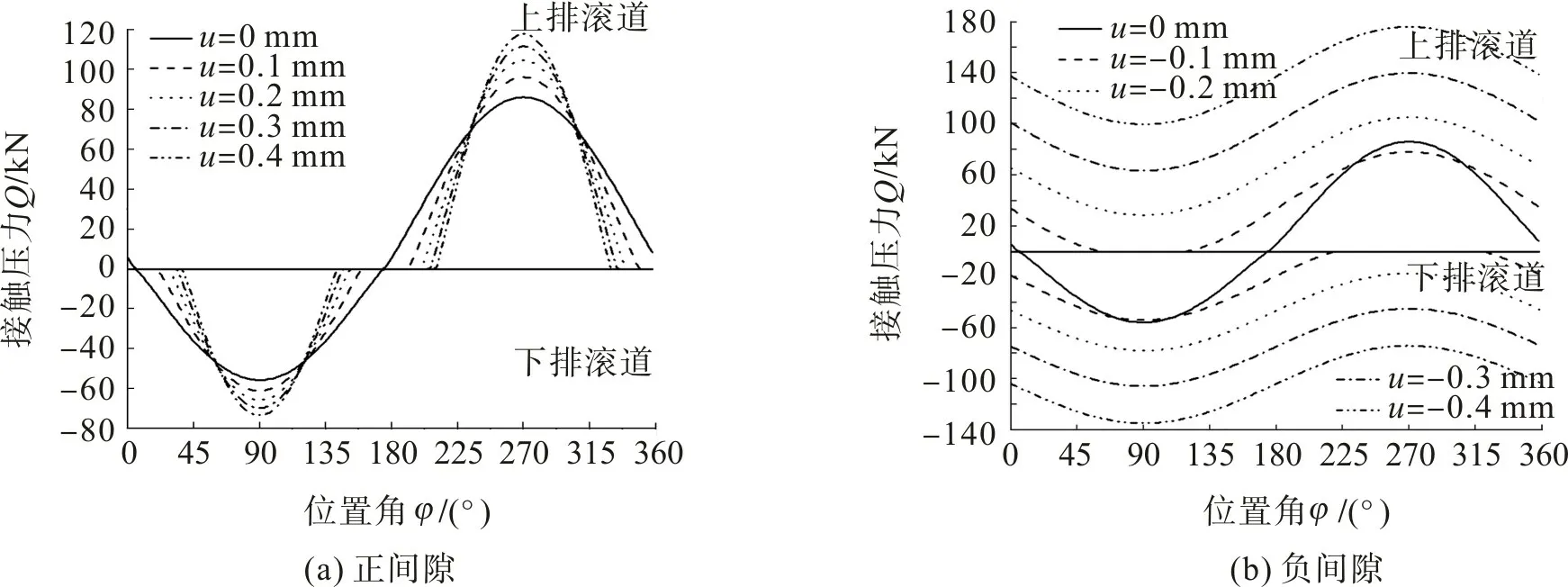
图4 间隙对滚道压力分布的影响Fig.4 Influence of clearance on the raceway load distribution
3.2.2 滚柱尺寸对摩擦力矩的影响
图5为回转支承外载荷及其他参数不变时,滚柱长度对回转支承摩擦力矩的影响。由图5可看出,摩擦力矩随着滚柱长度的增大而增大,这是因为当滚柱长度增加时,滚柱两端的相对滑动加剧,由此引起回转支承的摩擦力矩呈增大趋势。图6为回转支承外载荷及其他参数不变时,滚柱直径对回转支承摩擦力矩的影响。由图6可知,摩擦力矩随着滚柱直径的增大而减小,减小幅度随滚柱直径增大而逐渐降低。这是由于随着滚柱直径的增大,滚柱与滚道之间的微滑动会减弱,导致摩擦力矩降低。
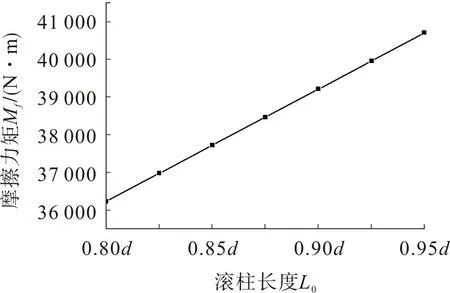
图5 滚柱长度对摩擦力矩的影响Fig.5 Influence of roller length on friction torque
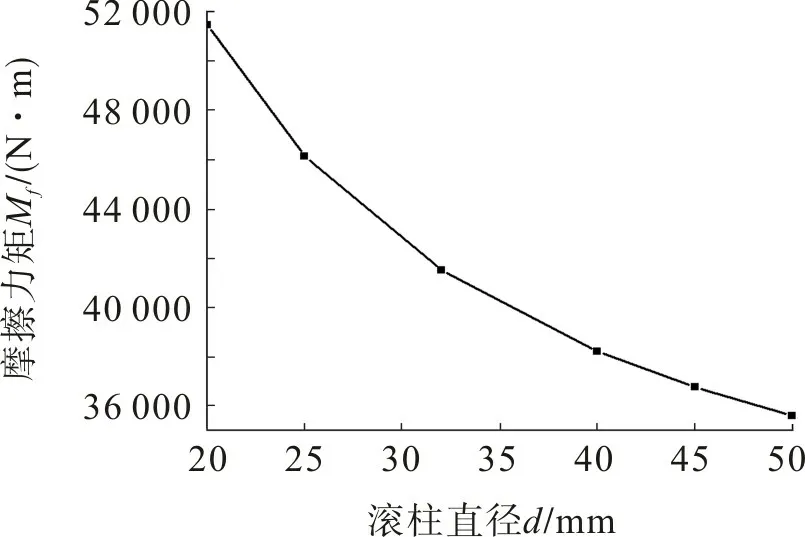
图6 滚柱直径对摩擦力矩的影响Fig.6 Influence of roller diameter on friction
上述针对滚柱尺寸引起的回转支承摩擦力矩变化分析中,分别只单独考虑滚柱长度、滚柱直径两个因素的影响。但是,在三排滚柱式回转支承的实际应用中,各排滚柱的直径和长度并不是随意组合而成,其常用的滚柱直径组合及滚柱长度分别如表2,3[26]。
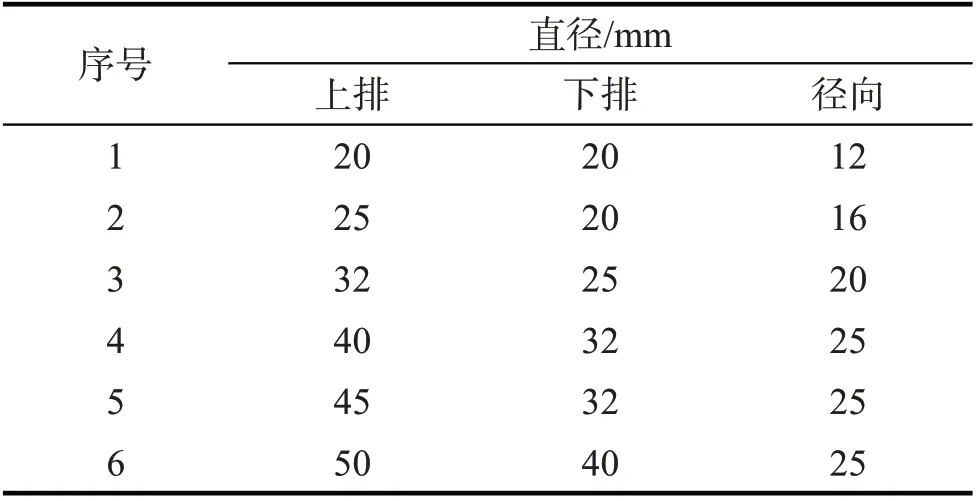
表2 上下排和径向滚柱直径组合Tab.2 Upper,lower row and radial roller diameter combination

表3 滚柱直径与滚柱长度Tab.3 Diameter and length of the roller
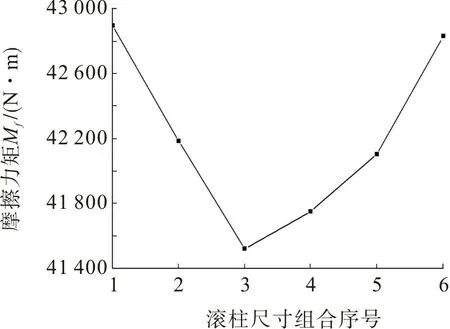
图7 滚柱尺寸组合对摩擦力矩的影响Fig.7 Influence of roller size combination of friction torque
以工程中常用的上下排和径向滚柱直径组合为研究对象,即上下排和径向滚柱直径组合为表2 中的组合序号1~6,与之对应的滚柱长度取值见表3,探讨回转支承外载荷及其他结构参数不变时,不同滚柱尺寸组合对摩擦力矩的影响,图7 为型号131.32.2000.00Z的回转支承摩擦力矩与不同滚柱尺寸组合之间的关系曲线。由图7 可知:随着滚柱尺寸的增大,摩擦力矩先减小后增大,这是因为滚柱尺寸较小时,滚柱直径增大引起的摩擦力矩降低幅度要大于滚柱长度增大引起的摩擦力矩增加幅度;滚柱尺寸增大到一定值后,滚柱直径对摩擦力矩的影响随之减弱,而滚柱长度对摩擦力矩的影响呈线性关系,故当滚柱直径继续增大时,摩擦力矩也随之增加。因此,在满足回转支承承载要求的前提下,应合理选择滚柱的尺寸组合,以减小回转支承的摩擦力矩、降低能量损耗。由图7 还可看出,对于型号为131.32.2000.00Z 的回转支承,采用表2 中序号3 的滚柱直径尺寸组合(上下排和径向滚柱直径为32,25,20 mm,长度为31.3,24.4,19.6 mm)摩擦力矩最小。
4 结果验证
在三排滚柱式回转支承的摩擦力矩计算中,一般先通过叠加法求出当量载荷或滚道压力分布,后计算其摩擦力矩。文献[10]中通过压力叠加法得到滚道压力分布,并给出回转支承的摩擦力矩公式,将本文计算结果与采用文献[10]中计算方法所得结果进行对比验证。以型号为131.32.2000.00Z 的三排柱回转支承及表1 参数为例,利用本文方法和文献[10]中的计算方法,计算上下排和径向滚柱与滚道之间的最大接触压力及回转支承的摩擦力矩,结果如表4。
由表4 可知,本文方法计算结果与文献[10]中计算方法所得结果相近,误差较小,表明本文计算方法可行。但文献[10]中计算方法只能分析零间隙情况下回转支承滚柱与滚道的接触压力及摩擦力矩,不能分析间隙、滚柱尺寸等结构参数对回转支承摩擦的影响。采用本文计算方法不仅可计算含任意间隙情况下滚柱与滚道的接触压力,且可分析三排滚柱式回转支承结构参数对其摩擦力矩的影响,故本文方法可为低摩擦力矩回转支承的参数设计提供一定参考。
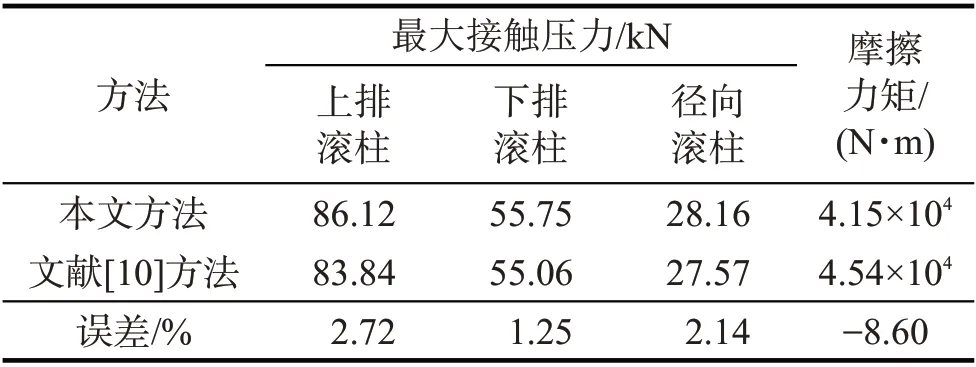
表4 计算结果对比Tab.4 Comparison of computation results
5 结 论
建立三排滚柱式回转支承静力学计算模型,在此基础上给出摩擦力矩计算公式,分析载荷及结构参数对三排滚柱式回转支承摩擦力矩的影响,得到如下主要结论:
1)三排滚柱式回转支承的摩擦力矩随外载荷的增大而增大,在相同当量轴向载荷情况下,轴向力对摩擦力矩的影响更为显著。
2)间隙在-0.4~0 mm之间变化时,摩擦力矩随负间隙绝对值的增大而急剧增大;间隙在0~0.4 mm之间变化时,摩擦力矩随之缓慢减小,但滚柱与滚道之间的接触载荷逐渐增大。
3)摩擦力矩随滚柱长度增大而增大,但随滚柱直径的增大而减小,对于行业中常用的滚柱尺寸组合而言,摩擦力矩随滚柱尺寸增大先减小后增大。因此在满足回转支承承载要求的情况下,应合理优化滚柱尺寸参数组合,以降低其摩擦力矩。
