基于频率控制的风电机组双曲线型塔筒优化分析
2020-10-10张国伟李钢强赵登利焦守雷陈江平王子月
文 | 张国伟,李钢强,赵登利,焦守雷,陈江平,王子月
随着国内风电装机容量的增加,风能资源较优、机组安装条件好的地方越来越少。为了弥补风能资源条件变差带来的成本增加,风电场需要安装具有更大风轮直径、更高塔筒的机组,以提升发电量。另外,风电机组共振表现为叶轮转动的激励频率与塔筒固有频率交叉或重合。当风轮运行于共振区间时,机组会因发生剧烈抖动而停机,不仅影响发电量,同时也会导致塔筒的破坏、叶片的断裂。根据机组设计应避免共振的要求,塔筒固有频率与叶片转动频率避振区间至少要超过5%。
影响塔筒固有频率的关键点主要有塔筒材质、结构尺寸、外部形状等。在塔筒材质、结构尺寸确定的情况下,外部形状对塔筒的频率影响较大。如图1所示,目前,市场中风电塔筒外观结构形式主要包括全锥型、变锥型、直锥型。这些结构形式无法满足塔筒直径较大、塔筒较重机组的避振要求。
为克服现有技术的不足,本文提供了一种基于频率控制的风电机组双曲线型塔筒,通过结构优化的设计方法在塔筒底、顶部法兰直径及塔筒高度与壁厚的限制条件下,以塔筒强度和频率为约束条件,采用多目标优化方法,寻求满足机组避振要求的最优双曲线形状。该塔筒形式可解决传统大直径钢塔频率较高的问题。
塔筒参数化优化
本研究针对某项目的大直径塔筒结构进行分析。由于进行本项目的塔筒设计时,基础设计已经完成,在顶部偏航结构无法更改、机组高度为100m的条件下,采用传统结构频率受限,因而开展优化设计,寻求满足要求的结构。采用有限元软件Design Exploration多目标驱动优化模块,建立塔筒参数化模型,以塔筒各筒节上下法兰直径及顶部筒节高度为参变量,塔筒一阶频率和筒节环焊缝最大应力为输出变量,寻求满足频率及焊缝应力要求的塔筒结构。根据Bladed载荷仿真分析经验,塔筒轮廓线型结构的变化对载荷影响较小,本文优化分析部分假定载荷不变,最终根据优化结果在Bladed中进行载荷迭代校对。
一、实验参数化分析
(一)参数化模型建立
筒体的有限元网格划分采用Solid186单元,旋转扫掠成整体有限元模型。本计算不考虑基础影响,底法兰采用固定边界约束其6个方向的自由度,无激励。机舱采用质量点加载,假定壁厚不变。塔筒参数化模型如图2所示。
塔筒高99400mm,底部直径6800mm,顶部直径5070mm,分五节,初设结构采用双锥型塔筒。本项目所用风电机组的一阶频率设计值满足0.270~0.279 Hz。塔筒具体参数化数值见表1,塔筒参数变量考虑塔筒制造、运输要求。
(二)不同参变量下的塔筒固有频率
设置参变量为D1/D2/D3/L1,输出值为P10(塔筒的一阶频率),通过控制变量,计算得到25组参数化结构,选取其中满足要求的5组,见表2。
由表2可知,通过减小塔筒各节直径,可得到满足塔筒一阶频率的塔筒结构。
(三)参变量与频率的变化关系
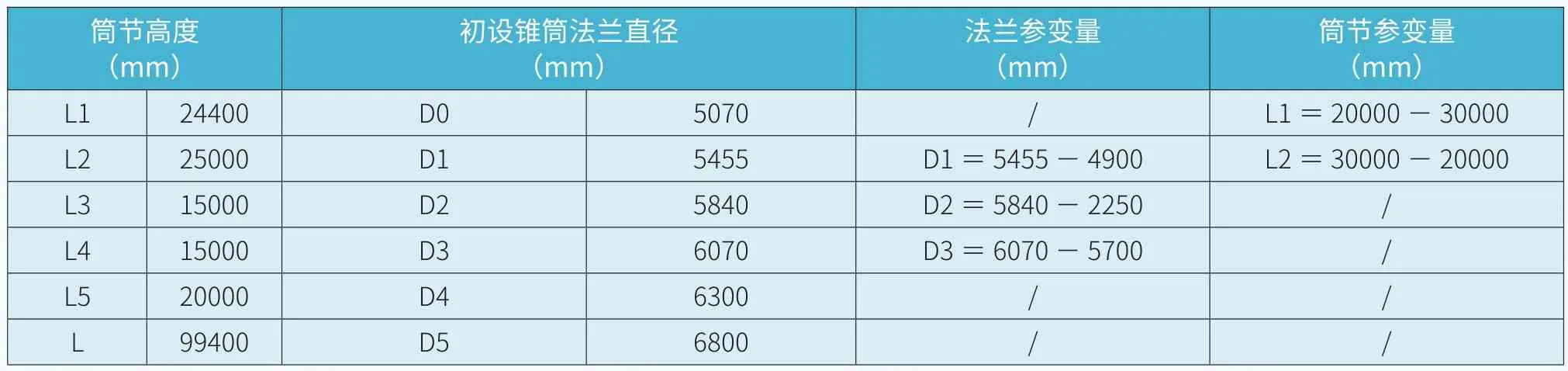
表1 塔筒参变量

表2 塔筒固有频率
输出参变量D1/D2/D3/L1与频率的关系,如图3所示。
由图3可知,随D1/D2/D3/L1的增大,一阶频率增大。其中,D1/D2/D3与频率呈近线性关系,L1与频率呈曲线关系,L1值越大,对频率的影响越小。
(四)参变量与频率敏感性的关系
输出参变量D1/D2/D3/L1与频率敏感性的关系,如图4所示。敏感性基于Spearman-Rank进行统计,同时考虑输入和输出参数的相关性。

表3 目标变量
由图4可知,各参变量与频率的敏感性由高到低的排序为:D2/D3/D1/L1。由此可知,减小塔筒中间段直径,更易降低塔筒固有频率。
二、目标参数优化设计
目标参数优化设计的具体方法为先设定输出结果的变化范围,再进行大量的参变量分析,计算得到最接近目标结果的参变量。
根据参变量与频率的敏感性分析结果,设定参变量为塔筒各段上下法兰直径,输出变量为塔筒固有频率和塔筒环焊缝处最大应力,参数化次数为1000次。具体目标变量见表3。
(一)目标参数结果
输出1000次优化结果中不同参变量对应的目标参数范围,不同参变量的频率值如图5所示,不同参变量的环焊缝最大应力值如图6所示。
由图5可知,1000次参变量优化结果中,仅有一小部分满足频率要求,随着参变量变化,整体频率分布呈现下降趋势。由图6可知,不同参变量下环焊缝的最大应力值范围为153MPa~221MPa,皆满足塔筒焊缝极限强度设计要求。
(二)目标参数分析
输出1000次优化结果中同时满足频率要求及环焊缝最大应力要求的目标参数范围,所有目标参数值如图7所示。
目标优化算法通过不同参变量插值组合计算,得到所有的目标参数值,并寻求同时满足目标参数的参变量组合。由图7可知,频率越小,对应的环焊缝最大应力越大;频率越大,对应的环焊缝最大应力越小,满足频率要求的参变量对应的环焊缝最大应力较大;PA、PB、PC值越大,塔筒固有频率越小,满足频率要求的参变量中,PB值的变化范围最小,PA值的变化范围次之,PC值的变化范围最大,且满足频率要求的参变量PB值对频率影响明显。整体对比可知,塔筒中上段法兰直径越小,频率越小。提取对应参变量数据,在满足频率设计要求、环焊缝最大应力较小时,参变量塔筒结构外形趋近于双曲线型。
(三)最终优化结构设计
考虑到优化后塔筒应力较大,需增加壁厚,选用频率最低的塔筒结构,具体尺寸见表4。
经过壁厚优化的塔筒固有频率为0.276 Hz,满足机组频率的设计要求。
根据优化结果,设计的塔筒结构形式为塔筒的整体外形近双曲线型,即连接各节塔筒的法兰直径符合双曲线结构要求—以塔筒中心线为y轴,塔筒径向方向为x轴,各筒节法兰直径尺寸满足双曲线要求。在满足强度校核情况下,通过控制双曲线的焦点和半实轴长可调整塔筒结构的频率。
根据运输条件及风电场发电要求,筒节数量不少于三节。一种五节筒节的双曲线型塔筒结构如图8所示,其由上下法兰和圆锥形筒节组成,各圆锥形筒节与各法兰焊接为圆锥形筒节。筒节一由法兰一、法兰二及圆锥型筒节一焊接成圆锥形筒节,法兰一由风电机组机舱确定,法兰二的直径小于法兰一的直径;筒节二由法兰二、法兰三及圆锥型筒节二焊接成圆锥形筒节,法兰三的直径大于法兰二的直径;筒节三由法兰三、法兰四及圆锥型筒节三焊接成圆锥形筒节,法兰四的直径大于法兰三的直径;筒节四、筒节五的结构设计方法参考筒节二。连接各筒节的法兰直径符合双曲线结构要求。
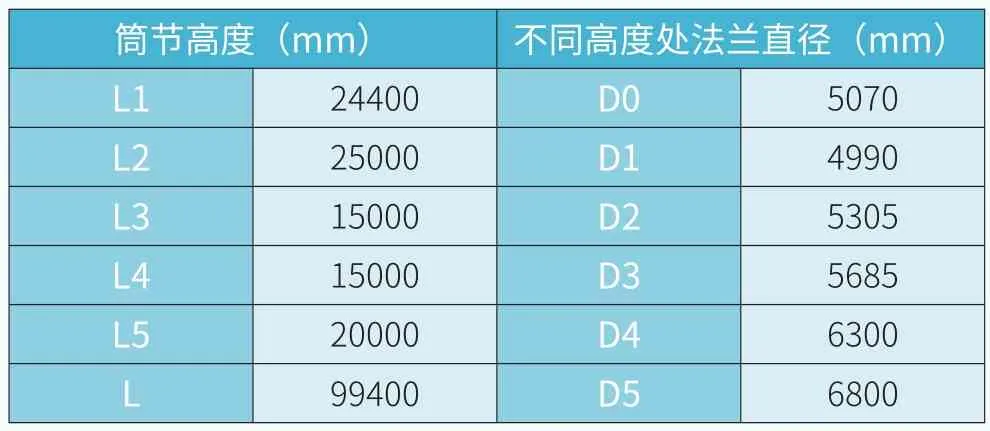
表4 塔筒尺寸
双曲线塔筒优化算法
通过多目标优化分析结果,得到满足工程需求的基于频率控制的塔筒双曲线结构。这里通过理论分析,得到基于频率控制的双曲线塔筒计算方法。
一、塔筒校核公式
根据风电机组设计要求,塔筒校核公式如下:
(1)双曲线塔筒外形投影的标准表达式为:
(2)频率要满足以下两个原则:
式中,fR为正常运行时的风轮最大转频,fR,m为m个叶片的跃迁频率,f0,n为塔筒的第n个固有频率。
(3)各焊缝极限强度要满足以下原则:
式中,SF为材料安全系数,σ为焊缝正应力,τ为焊缝切应力,fyk为材料许用应力。
(4)各焊缝疲劳强度要满足以下原则:
式中,ni,σ为应力范围σi所对应的循环次数,Ni,σ为应力范围σi所允许的循环次数,m为雨流计数后σi的个数。
(5)各筒体的屈曲要满足以下原则:
式中,σx,Ed为轴向压应力,σx,Rd为纵向设计屈曲应力,τxθ,Ed为剪切应力,τxθ,Rd为剪切设计屈曲应力,χx和χτ为标准中规定的相应屈曲折减系数。
二、塔筒固有频率计算
简化塔筒为悬臂梁,采用二节点梁单元进行有限元离散,设塔筒某一单元长度为l,单元密度为ρe,N为Hermite单元函数矩阵,E为弹性模量,I为截面惯性矩,A为单元截面面积。对任一单元,其质量矩阵me和弹性矩阵ket为:
由公式(7)、(8)可得:
塔筒无阻尼自由振动微分方程为:
其中,自有振动为简谐振动,令Y(t)=φsin(ωt+θ),φ是与时间无关的n阶向量,ω是振动圆频率,θ是初相位,得特征矩阵方程为:
上式为齐次线性代数方程组,有非零解的条件为系数行列式等于零,即:
通过计算可得系统的特征值矩阵和振型矩阵:
根据公式(9)―(15),可求得塔筒固有频率f0,n的值:
其中,单元截面积为:
式中,D为单元截面直径,t为单元截面的筒体壁厚。D值需满足公式(1),即:
根据运输及风电场机组要求,最大直径D值、塔筒总高度L值均为已知。由于筒体壁厚对频率的影响较小,设各节筒体壁厚t为固定值。确定双曲线焦点范围,采用多目标优化算法,满足公式(2)、(3)、(4)、(5)、(6)的要求,即可获得最优的双曲线型塔筒结构。
三、双曲线型塔筒优化算法
基于粒子群多目标优化方法,双曲线型塔筒优化流程如图9所示。粒子群寻优算法流程如图10所示,其具体包括:
(1)初始化n个焦点F1和半实轴长a的粒子群,位置范围设定为[c1-c2]和[a1-a2],速度范围设定为βm;
(2)判断焦点F1和半实轴长a粒子解的可行性,根据公式(9)、(10)、(12)、(13),进行塔筒固有频率和强度参数计算,并判断计算结果是否满足预设条件,即是否满足公式(2)、(3)的频率要求以及公式(4)、(5)、(6)的强度要求。如果有任一项要求未满足或固有频率和强度分析结果超出预设值,则以违反限制条件较小的粒子作为优化解;如果两个结果均在设计范围内,则以强度裕量最大的粒子作为优化解;
(3)根据优化解更新粒子的位置和速度。判断是否达到最大迭代次数,如果为“否”,则跳转至步骤(2)继续迭代计算;如果为“是”,选择满足塔筒固有频率和强度分析可行粒子解中强度裕量最大的粒子作为最优解,计算结束。
结论
本文针对某风电场塔筒结构进行分析,通过优化设计得到的双曲线型塔筒结构,解决了采用传统塔架结构无法满足频率要求的问题,并基于优化算法得到双曲线型结构的优化方法。具体得到以下结论:
(1)通过有限元软件进行塔筒实验参数化分析,得到塔筒中间段直径更易降低塔筒固有频率,中间段直径越小,频率越低。
(2)通过对塔筒频率及塔筒环焊缝最大应力计算分析可知,塔筒的频率越小,对应的塔筒环焊缝最大应力越大;塔筒的频率越大,对应的塔筒环焊缝最大应力越小。
(3)通过塔筒目标参数优化设计,得到1000次优化中,满足塔筒频率设计时,对应塔筒环焊缝最大应力较小的塔筒结构外形趋近于双曲线型。
(4)基于粒子群多目标优化方法,以频率和强度要求为约束条件,可得出基于频率控制的双曲线型塔筒优化计算方法。
