埃舍尔的不可能图形作品及其影响
2020-10-09周戭
周戭

摘 要:“不可能图形”的作品遵循线性透视法,而本质上是反透视的,就像一道需要观者参与的视觉谜语,吸引观者驻足凝视,画中所未呈现的部分才是谜底,这时候作品与我们经历的现实产生连接,构建出作品的深层寓意。
关键词:不可能图形;透视影响
中图分类号: J061文献标识码:A文章编号:2096-0905(2020)19-0-02
一、不可能立方体
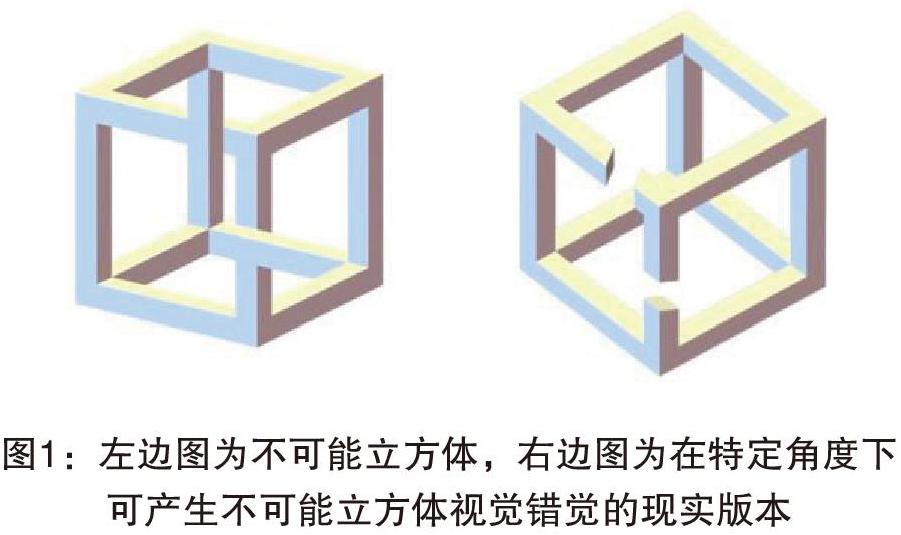
“不可能立方体”最早出现在荷兰版画家莫里茨·科内利斯·埃舍尔(Maurits Cornelis Escher)1958年的版画作品《观景楼》(Belvedere)中 (图1-图2),埃舍尔在《观景楼》所画的建筑柱廊前后错位,使其在同一坐标系下产生两个前后坐标互相矛盾的视觉冲突,但又不容易被观者直接察觉。人们曾试图用计算机模拟出观景楼的模型,结果证明这是一个现实里不可能存在的结构。在《观景楼》画面下方,埃舍尔绘制了一位坐在长凳上,手拿着“不可能立方体”的人,还单独绘制过一幅木刻版画。他曾经在一次演讲中谈道:“如果你想要用某种不可能存在的事物唤起注意,你首先要迷惑自己,然后才是观众。你要使不可能的元素尽量隐蔽,以至只满足浮光掠影的观众注意不到。这里必须有某种秘密,而它不能一眼被看穿。”“不可能图形”的作品从根本上动摇了自文艺复兴阿尔贝蒂·利昂纳·巴蒂斯塔(leon Battista Alberti)提出的线性透视法具有对现实“可公度”的信念。[1]
二、彭罗斯三角与彭罗斯阶梯
1934年,“不可能图形之父”瑞典艺术家雷乌特斯瓦德(Oscar Reutersvrd)最初创作了彭罗斯三角(Penrose triangle)图形。英国的精神病学家列昂尼尔·S·彭罗斯(Lionel Penrose)和他的儿子,数学家罗杰尔·彭罗斯 (Roger Penrose)在50年代设计并推广了这个三角形。埃舍尔著名的版画作品《瀑布》(Waterfall)正是基于彭罗斯三角原理。水流被建筑中的齿轮带动,沿着河道向上流动,最终从高处又倾泻到起初的原点,形成一个永远流动的循环系统。如果仔细注意河道上下层的空间构成,会发现这是现实中不可能建立的空间。
彭罗斯三角和彭罗斯阶梯曾被借用于电影《盗梦空间》(Inception)的清醒梦境(Lucid dream)的场景中,英国导演克里斯托弗·诺兰(Christopher Nolan)是近来为数不多的坚持胶片拍摄并大量运用物理特效的导演。在清醒梦境场景中,诺兰搭建出只有在特定的景况视角内才能呈现出的彭罗斯阶梯。
三、莫比乌斯带与克莱因瓶
1858年德国数学家、天文学家莫比乌斯(Mbius)和利斯廷(Johann Benedict Listing)各自独立的发现了莫比乌斯带(德语:Mbiusband),也称莫比乌斯环。这个结构可以用一条纸带旋转半圈再把两头连接来制作。它只有一条边和一个面,沿着面的轨迹延伸可以直接到达它的反面,形成永远没有终点的无限循环路径。当莫比乌斯带被从中分开两段时也不会断开,仍然保持各自完整性。莫比乌斯带是几何拓扑学中非常著名的例子。
几何拓扑学是19世纪出现的一门数学分支,关注于空间扭曲后仍然不变的性质。莫比乌斯带也常被看作是无穷大符号“∞”的来源,但实际上“∞”的出现要比莫比乌斯带更早。与莫比乌斯带非常相近的还有一个几何学物体克莱因瓶(KleinscheFlasche),最初是由德国数学家菲利克斯·克莱因(菲利克斯·克莱因)提出。克莱因瓶可由两个莫比乌斯带粘贴而成。这个瓶子没有边,既没有内部也没有外部,它的表面不会终结。克莱因瓶的瓶颈和瓶身是相交叉的,其实这是一个在四维空间中才能真正表现出来的曲面,瓶颈需要先穿过第四维空间然后才和瓶底圈相连,并不穿过瓶壁。现实中的克莱因瓶是四维空间在三维空间中的投影。
莫比乌斯带、克莱因瓶这类经典错视图式,都通过不可能图形暗示出往复循环的时间,是自然语言和形式语言中的自指(Self-reference)的几何化示例。自指是指通过一个句子直接或间接的提及自身。自指还可以由某种编码反应自身,常常造成悖论。例如我国流传很广的童谣:“从前有座山,山里有座,庙里有个老和尚正在给小和尚讲故事,讲的什么呢……”这就是一个自指的句子。自指在数学和计算机科学中也被称为递归(Recursion),指在函数的定义中使用函数自身的方法,自指也是分形理论(Fractal)的基石。
四、德洛斯特效应
德罗斯特效应(DrosteEffect)是指一幅图像的某个局部与整体图像类似,而图像中的局部又与更小的部分相似,依次类推循环往复。德罗斯特效应源于创立于1863年的荷兰第一大巧克力品牌德洛斯特(Droste)。1904年,艺术家让·米塞尔(Jan Misset)为这家巧克力品牌的可可粉包装盒设计了一幅包装插图,图中,一位护士手中拿着盛有德洛斯特巧克力包装盒和杯子的托盘。包装盒的图案与整张图片相同。这幅包装图开始变得家喻户晓,在数十年间也经历不同版本的调整诗人及专栏作家Nico Scheepmaker在七十年代开始使用“德罗斯特效应”这一词语。实际上,这一图式最早可能追溯到中古世纪的书籍或窗户的图案。在文艺复兴早期,意大利画家乔托(Giotto)在1320年绘制的《史特法尼斯基三联画》(Stefaneschi Triptych)中可以看到,枢机主教吉雅科莫·盖塔尼·史特法尼斯基(Giacomo Gaetani Stefaneschi)手持着与原画同样的三联画献给圣彼得。在现实中,也可以使用两面相互平行的镜子来产生的罗斯效应。[2]
完美的德罗斯特效应图式只存在于理论中,在现实中由于受制于画布有限的面积,重复的图像以等比例数列的方式递减,最终会因尺寸太小而终止。但是德罗斯特效应的动态展示体现出数字技术的优势。由计算机根据数学与物理原理在递归的基础上营造的虚拟世界中,德罗斯特效应能够由大至小无限的递减下去。德罗斯特效应也是自指系统的几何示例。虽然分形艺术的概念始于20世纪80年代。但早在1904年,瑞典数学家冯·科克(VonKoch)就提出了科克曲线(Koch Curve)的概念。一条直线经过等边三角形无限细分,最后就形成了复杂精细的雪花曲线。这一年,也正是艺术家米塞尔为德洛斯特设计了可可粉包装盒。德罗斯特效应也可看作分形艺术的雏形了。[3]
德罗斯特效应图式包含两种基本范式,第一种是“回”形范式,其结构像“回”字类似同心圆。第二种是“海螺”形范式,其结构像螺旋。这两种范式既有相似性也有区别。数理原型是设计图像所运用到的数学、物理等科学原理。
曾经是建筑师的阿根廷观念艺术家莱安德罗·艾利希(Leandro Erlich)非常善于对建筑空间进行改造,他的作品结合了大型互动装置、影像装置、摄影等多种创作形式,通过错视手法对日常景象进行改造,挑战着人们对生活“约定俗成”的认知。如《试衣间》(Changing Rooms)、《美发沙龙》(Hair Salon)、《电梯迷宫》《Elevator Maze》等装置作品都是“回”形范式的德罗斯特效应的体现。
五、结束语
埃舍尔的作品虽然涉及了一些“数学性”问题,如拓扑几何、不可能立方体、莫比乌斯带、彭罗斯阶梯、黎曼曲线等,但是他本人并不在意这些数学问题如何归类,更看中的是通过具象的可辨识的形象挖掘出蕴含的诗情。正如他所说:“我可以大言不惭地说,我能够享受到这种完美,并见证它的存在。因为它并不是我的發明,甚至也不是我的发现。数学法则完全不是人类的发明和创造。它们就“在那儿”,它们完全独立于人类的智慧而存在。一个人无论有多么聪明的才智,他所能做的,最多也只是把它们找出来,并给予确认。”
参考文献:
[1]李升锐,蓝江平,张志.埃舍尔视觉错视图形的艺术表现[J].设计, 2019,32(11):148-149.
[2]陈娜娜.视错觉在现代绘画中的应用[D].西北大学,2019.
[3]唐泓.论视错觉在艺术创作中的重要性[D].中国美术学院,2016.
