永磁同步电机矢量控制系统仿真实验设计
2020-10-09周晓华蓝会立廖凤依吴国强
周晓华,蓝会立,王 晨,张 银,杨 叙,廖凤依,吴国强
(广西科技大学 电气与信息工程学院,广西 柳州 545616)
永磁同步电机(permanent magnet synchronous motor,PMSM)具有结构紧凑、转矩惯量比高、功率密度和功率因数大,以及动态特性好等优点,在工业、交通、航空、军事等领域得到了广泛的研究和应用[1-2]。永磁同步电机的矢量控制是高校电机控制技术课程的核心内容之一,但由于所涉及的电机原理、坐标变换、自动控制原理、电力电子技术等理论知识比较抽象,学生难于理解和掌握。笔者利用Matlab/Simulink 仿真平台,设计了永磁同步电机电流滞环跟踪调制矢量控制和空间矢量脉宽调制(space vector pulse width modulation,SVPWM)矢量控制的仿真实验。通过电机起动、参考转速及负载转矩变化等动态过程的仿真实验教学,激发了学生的学习兴趣,加深了学生对永磁同步电机矢量控制系统的理解和应用,提高了教学质量。
1 PMSM 矢量控制原理
无阻尼绕组永磁同步电机在转子d-q坐标系下的定子磁链方程为
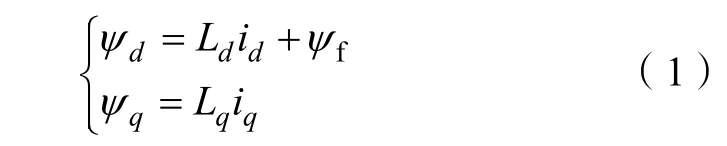
式中:ψd、ψq分别为d、q轴定子磁链分量;Ld、Lq分别为定子d、q轴等效电感;id、iq分别为d、q轴定子电流分量;ψf为转子永磁励磁磁链。
定子电压方程为

式中:ud、uq分别为d、q轴定子电压分量;Rs为定子电阻;p为微分算子;ω为转子角速度。
电磁转矩方程为

式中:pn为电机极对数。
将式(1)代入式(3)可得
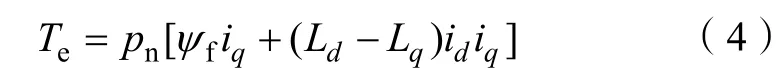
运动方程式为
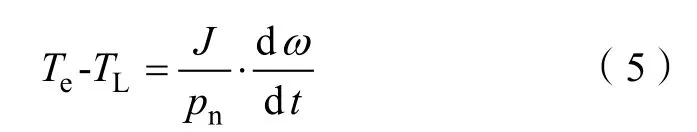
式中:TL为负载转矩,J为转动惯量。
改革开放初期至1997年是房地产估价行业的诞生和起步阶段。期间,计划经济向市场经济转型,政府部门相继出台有关房地产产权交易等方面的法律法规,国家诸多经济改革行为也随之涉及并产生房地产估价的需要。1994年出台《城市房地产管理法》,规定实行房地产价格评估制度以及房地产价格评估人员资格认证制度,从1995年起,开始实施房地产估价师执业资格制度。
由于ψf保持恒定,由式(4)可知,通过控制d、q轴定子电流分量id、iq就能有效控制电机的电磁转矩。电机稳态运行时,ψd、ψq可看作常数。在基频以下的恒转矩工作区,若控制定子电流矢量使之落在q轴上,即id=0、iq=is,并将式(1)代入式(2)可得永磁同步电机的简化定子磁链方程、定子电压方程及电磁转矩方程为

式中,is为定子电流幅值。
由式(8)可知,由于ψf保持恒定,通过控制is就可以控制电机电磁转矩,从而获得较好的静、动态性能。由于控制过程中始终保持d轴定子电流分量id=0,而仅对q轴定子电流分量iq进行控制,故也称id=0 控制[3-4]。
2 PMSM 矢量控制系统结构
电流滞环跟踪调制矢量控制系统结构如图 1 所示。转速给定值n*与转速实际值n的偏差经PI 转速调节器调节后,输出与电磁转矩Te成正比的q轴定子电流分量给定值与d轴定子电流分量给定值经2r/3s 坐标变换后得到电机定子三相电流给定值电流滞环脉冲发生器根据与定子三相电流实际值iabc的误差信号产生PWM 逆变器的6 路脉冲信号,从而驱动电机运行。

图1 电流滞环跟踪调制矢量控制系统原理图
若转子d轴超前定子A轴的电角度为θ,根据2r/3s坐标变换关系,并考虑到零轴定子电流分量i0=0,电机定子三相电流给定值可由下式计算:


电流滞环跟踪调制矢量控制系统原理简单,且不依赖于电机参数,鲁棒性好;但逆变器开关频率会随电机运行状况发生变化。SVPWM 可使逆变器具有固定的开关频率[5],其矢量控制系统结构如图2 所示。

图2 SVPWM 调制矢量控制系统原理图
转速给定值n*与转速实际值n的偏差经PI 转速调节器调节后,输出q轴定子电流分量给定值与q轴定子电流分量实际值iq的偏差经PI 电流调节器调节后,输出q轴定子电压分量给定值d轴定子电流分量给定值与d轴定子电流分量实际值id的偏差经PI 电流调节器调节后,输出d轴定子电压分量给定值d、q轴定子电流分量实际值id和iq可由测量得到的三相定子电流iabc经 3s/2s 和 2s/2r 变换得到。经 2r/2s 变换后得到定子电压的α、β轴分量给定值经 SVPWM 调制后得到PWM 逆变器的 6 路开关信号,从而实现对电机的运行控制[6]。
3 PMSM 矢量控制系统建模
3.1 电流滞环跟踪调制矢量控制
在Malab/Simulink 仿真平台建立的PMSM 矢量控制系统仿真模型如图3 所示。两种矢量控制系统的永磁同步电机参数相同,如表1 所示。

图3 电流滞环跟踪调制矢量控制系统仿真模型

表1 永磁同步电机参数
图 3 中,PI 转速调节器参数设置为:Kp=0.05,Ki=8。子系统 Subsystem 按式(10)进行计算以实现的 2r/3s 坐标变换,Generation 为电流滞环跟踪调制模块,滞环宽度设置为0.1。电机测量模块输出的转子空间位置角是q轴超前定子A轴的机械角度,需先转换为电角度,然后减去π/2 以得到d轴超前定子A轴的电角度θ[7]。
3.2 SVPWM 调制矢量控制
SVPWM调制矢量控制系统仿真模型如图4 所示。PI 转速调节器参数与电流滞环跟踪调制矢量控制系统相同。2 个PI 电流调节器参数采用内膜控制原理设计[8-9]且相同:Kp=17.85,Ki=6037.5。
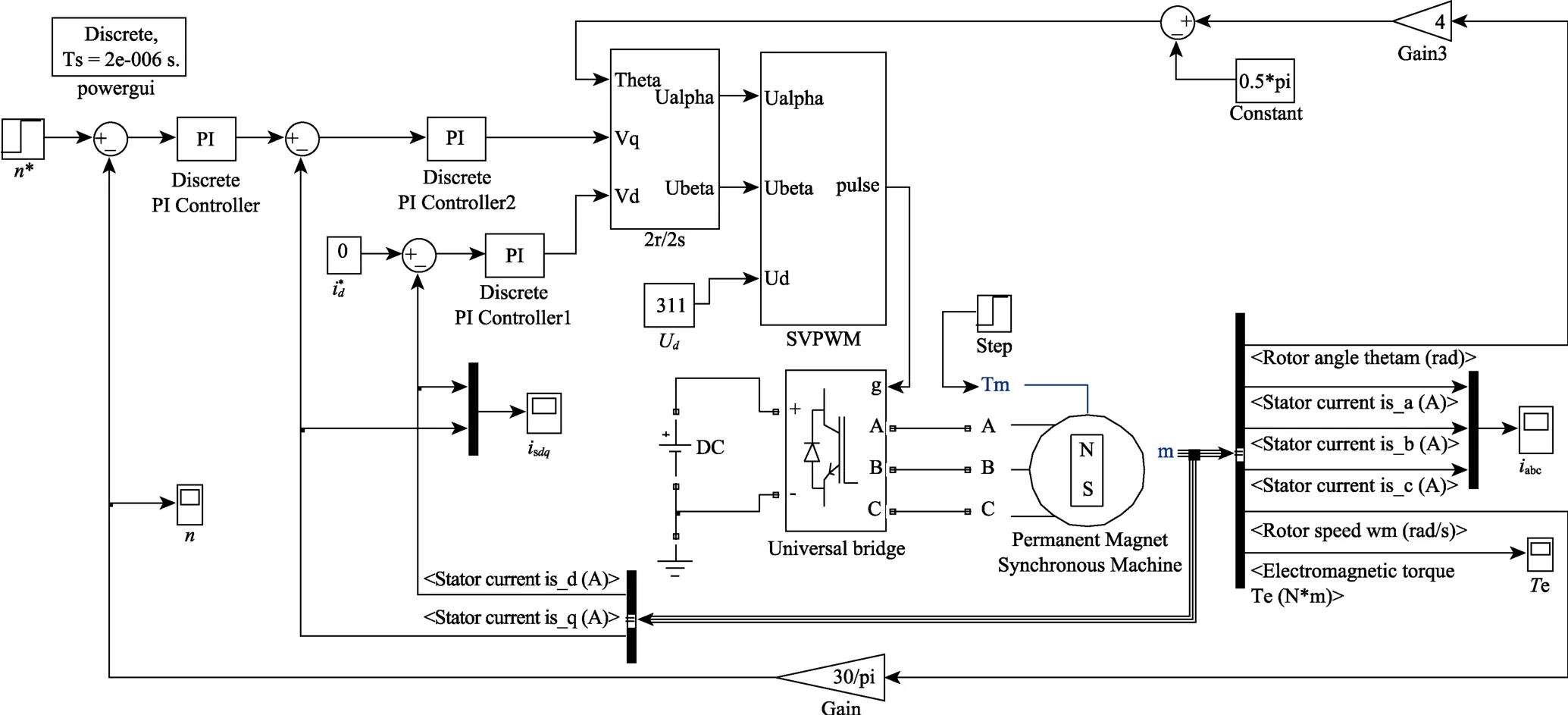
图4 SVPWM 调制矢量控制系统仿真模型
SVPWM 调制模块主要由参考电压扇区判断模块、相邻电压矢量作用时间T1、T2计算模块、扇区电压矢量切换时间Tcm1、Tcm2、Tcm3计算模块及脉冲产生模块构成。参考电压扇区判断模块根据由定子电压α、β轴分量Uα、Uβ所定义的电压U1、U2和U3的正负情况,即可判断参考电压Uref所处的扇区N。首先,定义电压U1、U2和U3[10]如下:

再定义开关函数Sk[11]:

则Uref所处扇区N可由下式[12-13]确定

相邻电压矢量作用时间T1、T2的计算可由中间变量X、Y、Z确定,其对应关系如表2 所示。
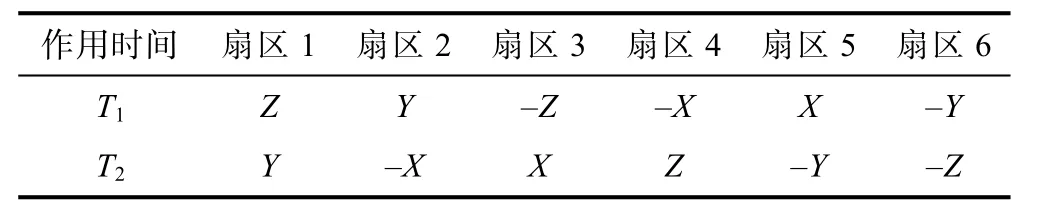
表 2 T1、T2 与 X、Y、Z 对应关系
表2 中,X、Y和Z定义如下

当T1+T2>Ts时,则T1、T2按下式计算
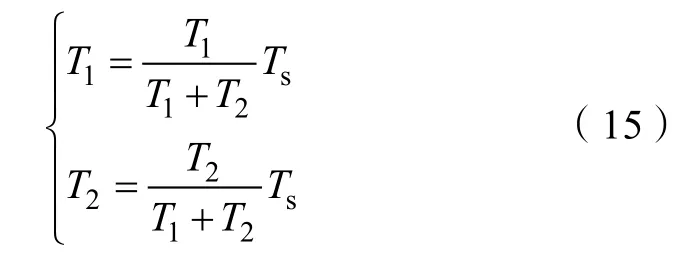
扇区电压矢量切换时间Tcm1、Tcm2、Tcm3则由时间变量Ta、Tb和Tc确定,其对应关系如表3 所示。

表 3 Tcm1、Tcm2、Tcm3 与 Ta、Tb、Tc 对应关系
表 3 中,Ta、Tb和Tc定义如下
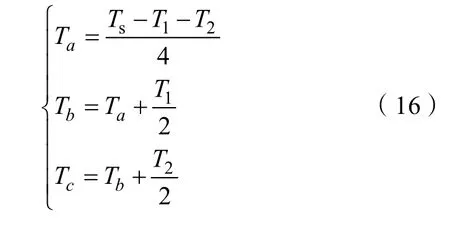
脉冲产生模块将扇区电压矢量切换时间Tcm1、Tcm2、Tcm3与三角波进行比较可得到 SVPWM 的输出时序,并产生PWM 逆变器的6 路开关信号[14]。
4 PMSM 矢量控制系统仿真实验
电机带负载转矩 4 N·m 起动,转速给定n*=600 r/min,当电机运行到0.04 s 时,负载转矩增加到10 N·m,当t=0.08 s 时,转速给定由600 r/min 上升到800 r/min,可观察电机起动、加速及控制系统抗干扰等性能。
4.1 电流滞环跟踪调制矢量控制仿真
图5 所示为电机转速波形。当电机转速由0 上升到给定转速600 r/min,再从600 r/min 上升到800 r/min时,虽有一定超调,但动态响应速度较快。在0.04 s负载转矩增加时,电机转速下降,但能快速恢复到给定转速值,说明系统抗扰动性能较好。
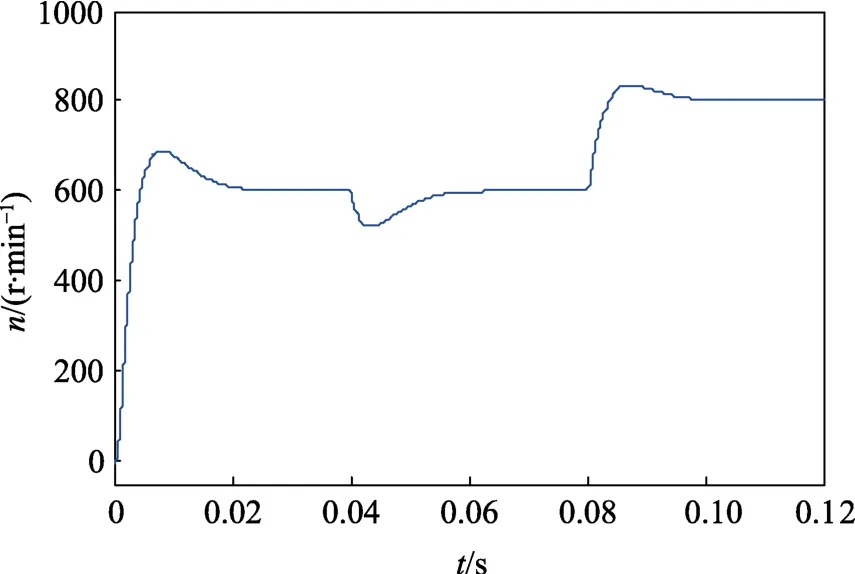
图5 电机转速响应波形
图6 为电磁转矩Te和定子电流q轴分量给定值波形。t=0.01 s 前为电机带负载起动状态,Te迅速上升至30 N·m 左右,电机转速由0 开始上升。t=0.01 s 时,电机起动过程结束,Te下降至4 N·m,与负载转矩相平衡。t=0.04 s 时,由于负载转矩突增到10 N·m,Te由4 N·m 上升至10 N·m,再次与负载转矩保持平衡。t=0.08 s 时,电机给定转速上升,Te突增,电机转速升高,待转速到达给定转速后,Te下降至10 N·m,继续与负载转矩保持平衡。控制过程中,Te与变化基本一致,通过对iq的控制实现了对电机Te及转速的控制,与理论分析相吻合。
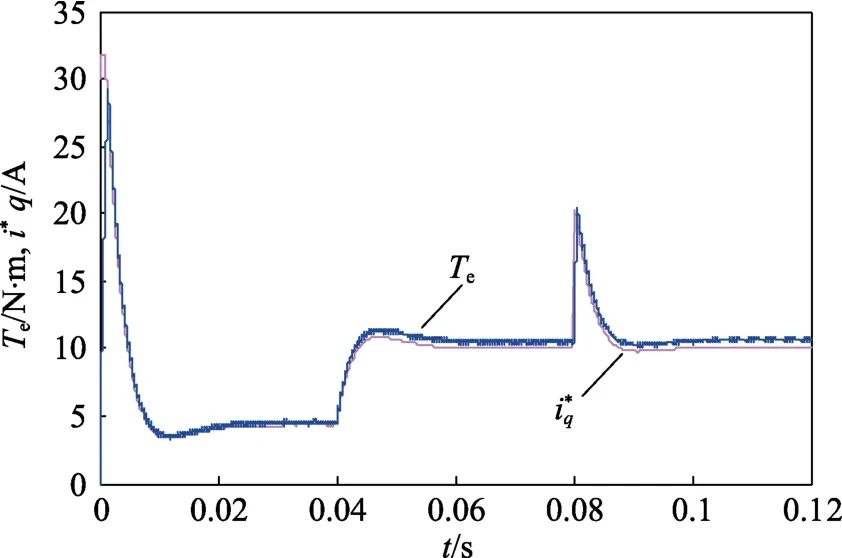
图6 电磁转矩与定子电流q 轴分量给定值波形

图7 定子三相电流给定值 波形

图8 定子三相电流实际值iabc 波形
图9 为电机定子电流d-q轴分量实际值id、iq波形,整个控制过程中,id始终保持为0,iq与给定值波形(图6)变化基本一致。
4.2 SVPWM 调制矢量控制仿真
图10—图13 分别为SVPWM 调制矢量控制系统电机转速、电磁转矩Te、定子三相电流实际值iabc和定子电流d-q轴分量实际值id、iq波形。其波形变化与电流滞环跟踪调制矢量控制系统对应波形基本一致,得到了较好地相互验证作用。

图9 定子电流d-q 轴分量id、iq 波形

图10 电机转速响应波形

图11 电磁转矩波形
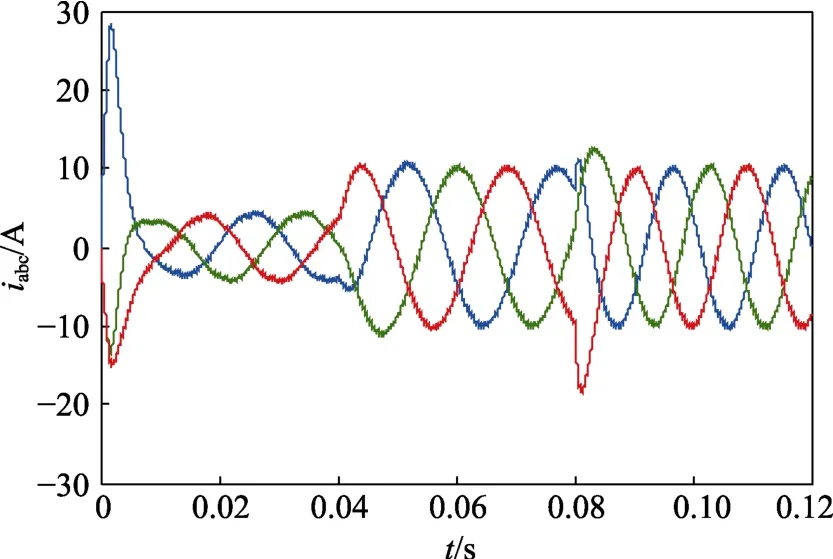
图12 定子三相电流iabc 波形
SVPWM 调制的关键在于参考电压扇区判断和相邻电压矢量作用时间的求取[15]。图 14 为扇区判断模块输出的扇区变化波形,扇区N由3→1→5→4→6→2交替变化,较好地实现了扇区的准确判断。
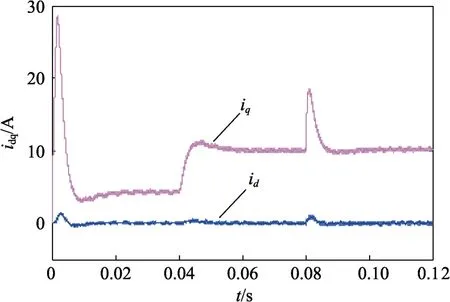
图13 定子电流d-q 轴分量id、iq 波形
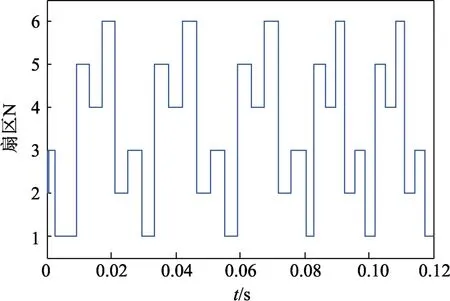
图14 扇区N 判断波形
图 15 为相邻扇区电压矢量切换时间Tcm1波形,其形状呈马鞍形,可有效提高直流电压的利用率并抑制谐波。
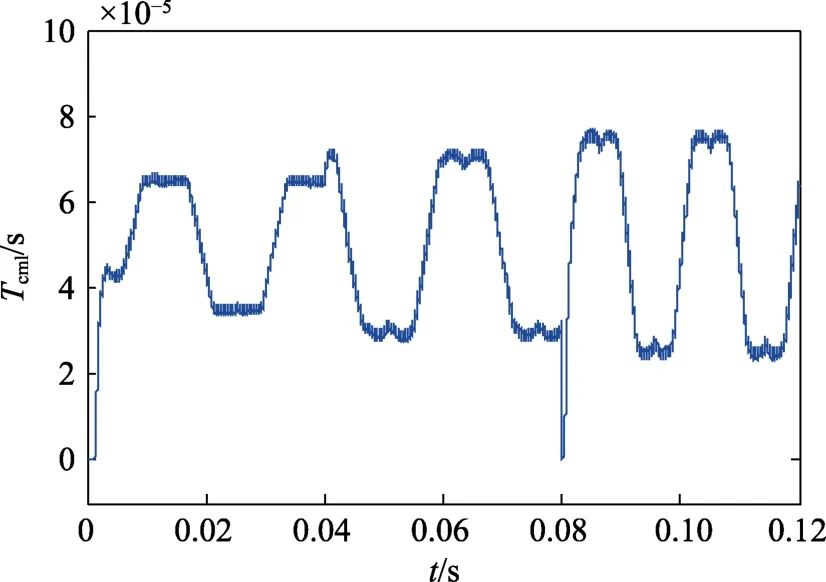
图15 扇区电压矢量切换时间Tcm1 波形
5 结语
通过对永磁同步电机负载起动、参考转速变化、突增负载转矩等情形进行的仿真实验,验证了所建立的永磁同步电机电流滞环跟踪调制矢量控制和SVPWM矢量控制仿真模型的正确性。通过开展仿真实验教学,能有效激发学生的学习和科研兴趣,加深学生对理论知识的理解,提高学生的综合应用能力和创新实践能力。
