基于Magnus 效应的摆动旋转圆柱实验教学平台

韩 阳，王 于，郭春雨，王 超，孙 聪

（哈尔滨工程大学 船舶工程学院，黑龙江 哈尔滨 150001）

基于 Magnus 效应的摆动旋转圆柱可以应用在很多工程领域，特别是在船舶减摇方面，传统的减摇装置有减摇水仓、减摇陀螺、减摇鳍、舭龙骨，但是这些传统的减摇装置有2 个局限性：一是所需的装置空间较大，二是不能进行全航速减摇。而基于 Magnus效应的摆动旋转圆柱可以解决以上问题。如何将理论知识更好地应用到工程实践中是一个值得思考的问题，为了解决该问题，本文设计了一种基于 Magnus效应的摆动旋转圆柱实验教学平台，该实验平台设计的重点是如何激发学生对基于 Magnus 效应的摆动旋转圆柱产生学习兴趣，并且理解抽象的理论知识，将理论知识更好地应用到工程实践中。基于 Magnus 效应的摆动旋转圆柱实验教学平台通过对不同形式的圆柱模型进行受力研究，分析了圆柱摆动角度、摆动速度、转速比、不同表面形状等因素对旋转圆柱产生升阻力的影响，将影响基于 Magnus 效应的摆动旋转圆柱升阻力特性的因素形象具体地向学生展示出来，使学生能够通过实验现象更好地理解和学习理论知识。同时，学生们参与实验可以培养其实践能力和创新思维，并且在实验过程中可以锻炼学生的合作意识，加强学生的动手操作能力，提高学生的科学严谨性，为社会发展培养优秀的全方位人才，该实验教学平台正是根据教育部相关的指导思想应运而出[1-4]。

1 Magnus 效应

Magnus 效应产生的是物体在流体中旋转，当物体一侧的旋转方向与来流方向相同时，这一侧的流体流速就会加快，当物体一侧的旋转方向与来流方向相反时，这一侧的流体流速就会减小，根据伯努利方程可知，速度增大时压强减小，速度减小时压强增大，旋转物体会因为两侧流体速度不同而产生一个与来流不同方向的压力差，这一压力差也称 Magnus 力（见图1），物体轨迹发生偏转正是由这一压力差因引起的。当有来流速度时，只需圆柱旋转就可以使圆柱下面的来流产生速度差从而产生升力；当没有来流速度的时候，就需要圆柱摆动来代替来流（见图 2）。Magnus效应是相对较难的问题，根本原因是其理论的抽象性，会给学生学习带来很多困难，不参考实验现象，仅仅通过理论学习无法理解其原理。为了使学生更好地理解学习 Magnus 效应，为未来解决工程问题奠定良好的基础，基于 Magnus 效应的摆动旋转圆柱实验教学平台是必不可少的[5-8]。

图1 Magnus 效应

图2 摆动旋转圆柱

2 基于Magnus 效应的旋转旋转圆柱

基于 Magnus 效应的旋转旋转圆柱在风力发电、推进、船舶减摇等方面有很重要的作用。特别是船舶减摇方面，船舶在航行过程中由于受到波浪的影响会产生横摇，船舶横摇会产生较大的侧倾运动，侧倾运动会增大航行阻力，影响船舶航行的安全性和船员工作的舒适性，因此减摇装置在船舶设计中是必不可少的，而基于 Magnus 效应的摆动旋转圆柱减摇装置结构简单，占用空间小，制造成本较低，并且在低航速和零航速条件下减摇效果显著，未来可广泛应用于各种船舶减摇。基于 Magnus 效应的旋转圆柱减摇装置的原理是在船舶两侧底部安装旋转旋转圆柱（图3），当有来流速度的时候，圆柱旋转方向和来流方向相同的一侧，来流的速度增大，压强减小；圆柱旋转方向和来流方向相反的一侧，来流的速度减小，压强增大，会产生压力差，从而产生升力，船舶左右2 个圆柱旋转方向不同，分别产生向上和向下的力，产生一个和船舶横摇力矩方向相反的力矩，从而达到减摇效果，当没有来流速度的时候，需要圆柱摆动来代替来流，从而达到减摇的效果[9]。杜雪[10]对基于 Magnus 效应的旋转旋转圆柱减摇装置的水动力特性进行了深入研究，研究结果表明，在低航速下该装置在具有良好的减摇效果。但该研究距形成产品具有较大的差距，所以设计基于 Magnus 效应的摆动旋转圆柱实验教学平台来提升相关技术储备进行相关基础研究是非常有必要的[11-14]。

图3 基于Magnus 效应的旋转圆柱减摇装置

3 基于 Magnus 效应的摆动旋转圆柱实验教学平台设计

3.1 实验模型和工况

实验的模型是直径为0.036 m 的长径比为7 的不同类型的圆柱，如图4 所示，从左往右依次为截锥圆柱、圆凸圆柱、光滑圆柱。

基于 Magnus 效应的摆动旋转圆柱实验教学平台对不同摆动速度、摆动角度、转速比、不同表面形状的圆柱模型进行实验，摆动角度依次为120°、150°、180°，实验工况见表1。

图4 不同长径比实验圆柱模型

表1 实验工况表

3.2 实验设备

3.2.1 流场结构

基于 Magnus 效应的摆动旋转圆柱实验是在哈尔滨工程大学三甲实验室循环水池中进行的，具体实验设备如图5 所示，循环水池试验段为矩形截面，尺寸为1.7 m（宽）× 1.5 m（高），流速由计算机控制，范围为0~3 m/s。

图5 循环水池

3.2.2 伺服电动机

伺服电动机相关参数如表2 所示。

表2 伺服电动机参数

3.2.3 圆柱连接装置

图6 是旋转圆柱连接装置图，包括六分力天平，天平的上端连接固定在循环水池上的横梁，天平的下端固定在钢板上，伺服电动机固定在钢板上，水下电机连接在伺服电机的轴上，将圆柱安装在水下电机上，由水下电机提供转速；由伺服电机带动圆柱摆动。

图6 摆动旋转圆柱连接装置图

3.3 实验流程

基于 Magnus 效应的旋转圆柱实验的流程包括以下几个步骤：

（1）摆动旋转圆柱实验前期准备；

（2）连接摆动旋转圆柱实验装置；

（3）对摆动旋转圆柱实验装置进行标定，确保实验的准确性；

（4）通过计算机调速器来调节伺服电机和水下电机的转速；

（5）调节圆柱的摆动角度；

（6）用动态信号采集仪采集数据；

（7）读取平稳段的数据并记录；

（8）分析数据，得出结论。

4 实验结果与分析

实验得到的数据经过一系列的处理，最终分析得出影响基于 Magnus 效应的摆动旋转圆柱升阻力特性的因素，图8 是摆动角度为120°时不同转速比和摆动速度对摆动旋转圆柱升力的影响，由图8 可以看出，升力随着圆柱摆动速度的增加而增加，这是因为摆动速度的增大能够使圆柱上下的来流速度差增大，根据伯努利方程可知速度差越大，圆柱上边表面的压力差就越大，因此随着摆动速度的增加圆柱的升力就越大。当摆动速度较低时（30~40 r/min），升力随着转速比的增加先增加然后趋于平稳；当摆动速度较高时（79~105 r/min），升力随着转速比的增大而增大。不同表面形式的摆动旋转圆柱变化趋势是相同的，这一点也验证了实验的准确性。图9 是摆动速度为92 r/min 时升力随摆动角度变化的趋势图，由图9 可知，随着摆动角度的增加，升力增加，这是因为当圆柱摆动到极限角度的时候会突然变向，这时会产生方向相反的升力，从而会抵消一部分升力，而产生相反升力的这一区间是一定的，随着摆动角度的增加，产生正向升力的区间增大，所以平均升力增大。通过此实验平台可以形象准确地展现出影响摆动旋转圆柱升阻力特性的因素，能够充分激发学生的学习兴趣，将理论和实践相结合，不仅能够提高学习效率，还能培养学生的创新能力。

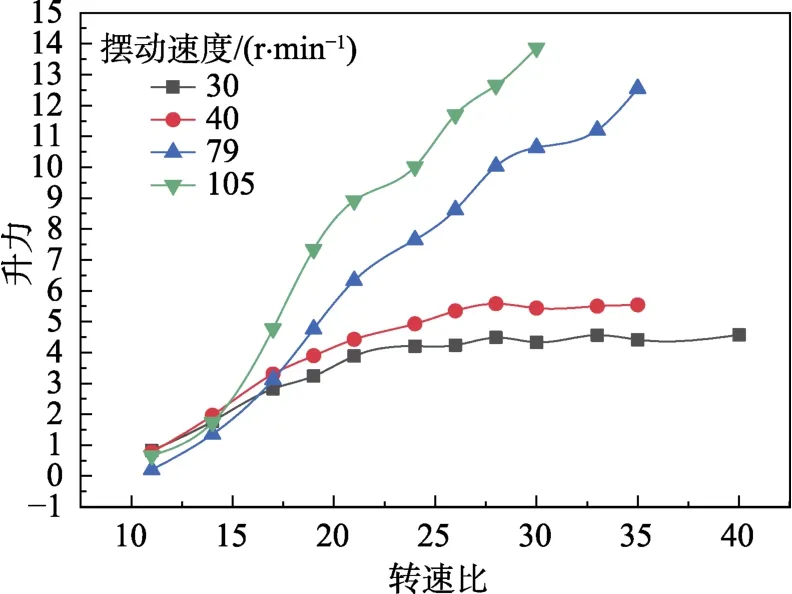
图8 摆动角度为120°时升力变化趋势

图9 摆动速度为92 r/min 时升力变化趋势

5 结语

本设计是一套基于 Magnus 效应的摆动旋转圆柱实验教学平台，该实验平台能够准确形象地演示出影响摆动旋转圆柱升阻力特性的因素，使学生能够简单快速地了解基于Magnus 效应的摆动旋转圆柱的原理，在理解理论的基础上，锻炼学生的实践能力，使其全方面发展。该平台具有综合性，不仅仅适用于摆动旋转圆柱，也可以模拟其他模型如减摇鳍、舵等的受力情况。