基于GA-MVFOSM法的DSA250型受电弓运动可靠性分析

曹 阳，李永华，吴永鑫

(大连交通大学机车车辆工程学院，辽宁 大连 116028)

0 引言

牵引供电系统作为轨道车辆的重要动力传输系统，是保证列车动力来源稳定的关键。受电弓作为牵引供电系统的核心部件之一，其工作可靠性会严重影响列车运行稳定性和安全性。随着列车运行速度的提高，受电弓工作条件逐渐恶化，对受电弓工作可靠性提出了更高的要求。因此，分析不确定性因素对受电弓工作可靠性的影响，对提高受电弓工作可靠性有重要意义。

受电弓的可靠性与其工作性能密切相关。受电弓工作性能越好，各杆件的运动轨迹越接近理想轨迹，受电弓的可靠性越高。目前，文献[1-7]对受电弓工作性能进行了研究，这些研究多以弓网系统的结构参数为属性建立模型，分析受电弓的工作性能是否满足实际要求。为探究受电弓的工作性能达到实际要求的程度，有学者对受电弓的工作可靠性进行了研究。张义民等[8]采用随机摄动法分析了受电弓在最大工作高度时的静强度可靠性及灵敏度；李永华等[9]采用GO法对受电弓系统进行了RAMS评估，得到了受电弓系统可靠性数据；李兴运等[10]和王远霏等[11]采用系统可靠性分析的方法对受电弓系统进行了研究，得到了受电弓系统可靠性水平。上述研究得到了受电弓系统在实际运行工况下的薄弱环节，得出载荷与材料参数对受电弓静强度可靠性的影响。除以上因素外，受电弓杆件尺寸的不确定性与运动副磨损会严重影响受电弓机构的运动轨迹，降低受电弓工作可靠性，造成弓网故障，威胁列车运行安全。

本文首先构建了DSA250型受电弓的运动学方程；其次根据Archard磨损理论与可靠性理论，考虑运动副磨损与杆件尺寸不确定性，建立了受电弓的磨损可靠性与运动可靠性模型；最后将遗传算法与一次二阶矩法相结合，求解受电弓运动可靠度，并分析了杆件尺寸不确定性与运动副磨损对受电弓工作可靠性的影响，为提高受电弓工作的可靠性提供一定参考。

1 受电弓运动学方程的建立

本文采用的DSA250型受电弓如图1所示。受电弓工作原理为：升弓气囊对下臂杆施加升弓力矩，使其绕运动副转动，同时下臂杆通过铰链的作用，带动拉杆、连杆和上臂杆绕着相应的运动副抬升一定的角度，带动弓头达到规定的工作高度。平衡杆和平衡臂则在列车运行中起到保持弓头转角不超过允许值的作用。

图1 DSA250型受电弓

为了保证受电弓在列车运行中可靠受流，弓头的运动高度必须高于允许最小运动高度，若低于最小值，会严重影响弓网受流质量，进而影响列车正常运行。因此，获取受电弓弓头运动高度表达式是受电弓运动可靠性分析的前提。考虑到受电弓工作特点及力学特性，可将其简化为平面连杆机构，如图2所示。

图2 DSA250受电弓机构简化图

由图2可知，弓头E点的运动学方程可表示为

yE=lBDsinα+lDEsinγ

(1)

yE为弓头运动高度；lBD、lDE分别为BD、DE的杆长；α、γ分别为BD、DE杆与水平方向的夹角。

2 可靠性模型的建立

根据受电弓工作要求，弓头的运动高度需达到规定工作高度，才可以从接触网获取电能，使列车有稳定的动力来源。受电弓机构在反复升降弓之后，受到杆件尺寸不确定性及运动副不同程度磨损的影响，弓头的运动高度会与规定高度有一定偏差，降低弓网受流质量，无法为列车提供稳定的动力，影响列车运行稳定性和安全性。因此,有必要分析磨损与杆件尺寸不确定性对受电弓运动可靠性的影响。

2.1 受电弓运动副磨损可靠性模型

受电弓连杆机构在运动过程中会出现运动副磨损，使运动副半径变大，降低机构的运动精度。根据Archard磨损理论，推导出运动副半径磨损量模型为

(2)

Δr为磨损半径变化量；n为运动周期，本文中表示一次升弓或降弓；k为磨损系数；φ为2个构件相对转过的角度；F为运动副的接触力；b为运动副的接触宽度；H为运动副材料的布氏硬度值。

由式(2)可知，运动副半径磨损量大小受材料参数k与H影响。在实际生产过程中，受加工工艺水平的限制及人为因素的影响，材料参数具有不确定性，从而使磨损量大小也存在不确定性。根据文献[12]，当运动副半径磨损量达到运动副初始半径r的0.003～0.006倍时，可认为该运动副失效，则运动副磨损可靠性模型为

(3)

μ[r]为半径最大允许磨损量均值，其取值范围为0.003r～0.006r；μk与μH分别为k与H的均值；σk与σH分别为k与H的标准差。

在实际运行中，受电弓受各种因素的影响使弓头脱离接触网的距离称为离线距离，当离线距离小于允许值时，才可以保证受电弓正常受流。由于各运动副的磨损，必然会导致弓头的运动高度有一定下沉。本文假设各运动副半径的磨损量之和等于弓头运动高度下沉量，则当下沉量小于允许最大离线距离时，可以保证受电弓正常工作。根据式(1)，弓头的运动高度与运动副B、D、E有关，则考虑运动副磨损的弓头运动可靠性模型为

(4)

i=B、D、E；dmax为允许最大离线距离。

2.2 受电弓运动可靠性模型

为进一步探究杆件尺寸不确定性对受电弓弓头运动可靠性的影响，将弓头运动高度yE与弓头因磨损而导致的下沉量作差可得

(5)

联立式(2)和式(5)，建立考虑杆件lBD、lDE尺寸不确定性的受电弓弓头运动可靠性模型为

β3=

(6)

μlBD与μlDE为lBD与lDE杆件的均值；σlBD与σlDE为lBD与lDE杆件的标准差；ymin为受电弓允许最小运动高度。

3 GA-MVFOSM法

受电弓运动可靠性的计算是基于可靠性理论，构建运动可靠性指标，再通过可靠度求解方法获取运动可靠度。可靠度求解方法主要有一次二阶矩法、蒙特卡洛法和高次高阶矩法。其中，一次二阶矩中心点法(mean value first order and second moment，MVFOSM)是工程上常用的可靠度求解方法，其原理是利用随机变量的特征值建立结构可靠度求解模型，再通过式(7)求得结构可靠度：

R=Φ(β)

(7)

R为结构的可靠度；Φ(·)为标准正态分布的累积分布函数。

MVFOSM法虽计算简便，精度较高，但当原功能函数较为复杂时，其计算结果往往与实际情况相差较大，如图3所示。图3中，β1为应用MVFOSM法求得的可靠性指标，β2为实际的可靠性指标；而且MVFOSM法展开点不一定位于原失效曲面上，会降低求解的精度。

图3 传统MVFOSM法的几何意义

为提高MVFOSM法的计算精度，本文提出了GA-MVFOSM可靠度求解方法，具体求解步骤如下：

a.建立结构的可靠性模型并确定随机变量的变化范围。

b.按照遗传算法的编码规则，对随机变量进行二进制编码并生成初始种群。

c.以结构的可靠性模型为适应度函数，计算个体适应度。

d.根据遗传算法的寻优原理，选取适应度高的个体进行遗传操作。

e.由式(3)～式(7)计算结构可靠度。

综上所述，基于GA-MVFOSM的受电弓运动可靠性分析流程如图4所示。

图4 受电弓运动可靠性计算流程

4 受电弓运动可靠性分析

4.1 仅考虑运动副磨损的受电弓运动可靠性分析

对于在线路上运行的受电弓，最危险的状态为弓头处于最大工作高度的状态。根据DSA250型受电弓技术参数，其最大工作高度为2 850 mm，设允许最大离线距离dmax为10 mm，允许最小运动高度ymin为2 840 mm。运动副B、D、E随机变量分布类型及参数如表1所示，允许最大磨损量如表2所示。

表1 随机变量分布类型及参数

表2 允许最大磨损量

为计算各运动副的磨损量，需先建立受电弓几何模型，仿真获取各运动副的接触力。在ADAMS/View中，受电弓各杆件应用连杆模拟，采用长方体与布尔运算的方式建立受电弓底架与弓头，在相应的运动副处挖孔、建立圆柱体并添加转动副约束来模拟实际运动副销轴，最后在运动副B处施加驱动力矩，设置仿真步长和仿真时间，模拟受电弓运动到最大工作高度。受电弓的几何模型如图5所示，通过仿真获取的各运动副接触力如图6所示。

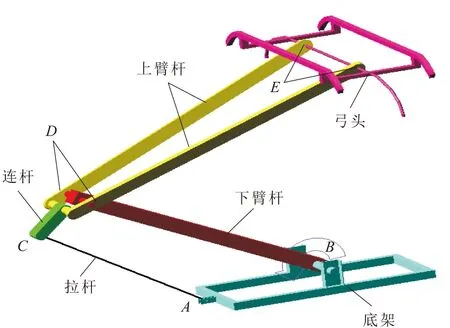
图5 受电弓几何模型

图6 运动副接触力

由图6可知，运动副B与D的接触力在0～4 s内逐渐减小，在4～8 s内变化比较平稳，而运动副E的接触力在0～8 s内变化均较小，且运动副B的接触力始终最大，运动副E最小。原因在于，受电弓开始升弓时需克服杆件自身重力作用，运动副B与D需较大的力来维持升弓状态，随着弓头逐渐达到规定高度，二者x向距离逐渐减小(如图1所示)，维持受电弓升弓状态的力逐渐降低并趋于平稳，在受电弓升弓过程中，运动副B承受除底架外所有杆件重量且受有升弓力矩，运动副D承受上臂杆与弓头的重量，而运动副E自始至终只需维持弓头处于上升状态，在升弓过程中，只需承受弓头的重量，且没有外力作用，其接触力最小且变化比较平稳。

将获取的各运动副接触力及已知参数代入式(2)，得到各运动副的半径磨损量如表3所示。由表3可知，各运动副的磨损量在GB/T 21561.1--2018规定的运动周期内，均未超过最大允许磨损量。由于运动副B的受力情况最复杂，其磨损量始终最大；运动副E的受力情况最简单，其磨损量始终最小；运动副D的受力复杂程度介于二者之间，其磨损量也始终介于二者之间。

表3 各运动副的半径磨损量

将表3数据代入式(3)得到各运动副的磨损可靠度，如图7所示。

由图7可知，当运动副B、D、E的磨损量分别在0～0.230 0 mm、0～0.136 6 mm、0～0.006 6 mm内时，各运动副的磨损可靠度较高，且下降速度缓慢；当各运动副的磨损量超过0.230 0 mm、0.136 6 mm、0.006 6 mm时，各运动副的磨损可靠度急剧下降。原因是当磨损量超过一定值后，各运动副半径变大，销轴之间的距离增加，接触力增大，使销轴表面接触点在局部高压力作用下产生黏合，在销轴相对滑动的过程中，由于接触表面切向力的作用，加剧了销轴表层材料的磨损，恶化了运动副工作环境，使运动副磨损可靠度急剧下降。与MVFOSM法相比，利用GA-MVFOSM法得到的可靠度结果偏于安全，且更接近受电弓真实的可靠度值。

根据表3提供的各运动副磨损量，计算受电弓运动过程中的总磨损量，并结合式(4)和GA-MVFOSM法得到弓头的运动可靠度，计算结果如图8所示。

由图8可知，随着运动副总磨损量的增加，弓头的运动可靠度呈现出近似线性的下降趋势。原因在于，在受电弓机构的主要使用期间内，各运动副处于稳定磨损阶段，此时运动副磨损速率恒定，运动副磨损量呈线性增加的趋势。弓头的运动可靠度均在0.99之上，处于较高水平，说明受电弓在1万次的运动周期中，弓头达到规定高度的可靠度水平较高。

图7 各运动副磨损可靠度

图8 仅考虑磨损的弓头运动可靠度对比

4.2 综合考虑杆件尺寸不确定性及运动副磨损的受电弓运动可靠性分析

为进一步探究杆件尺寸不确定性对弓头运动可靠性的影响，将4.1节获得的各运动副接触力与磨损量代入式(6)，并应用GA-MVFOSM法计算弓头运动可靠度。其中，各随机变量分布类型及参数如表4所示，弓头运动可靠度结果如表5所示。

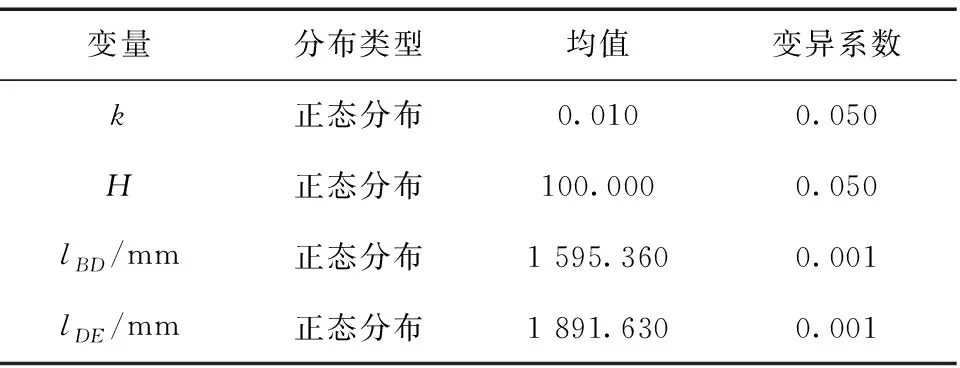
表4 各随机变量分布类型及参数

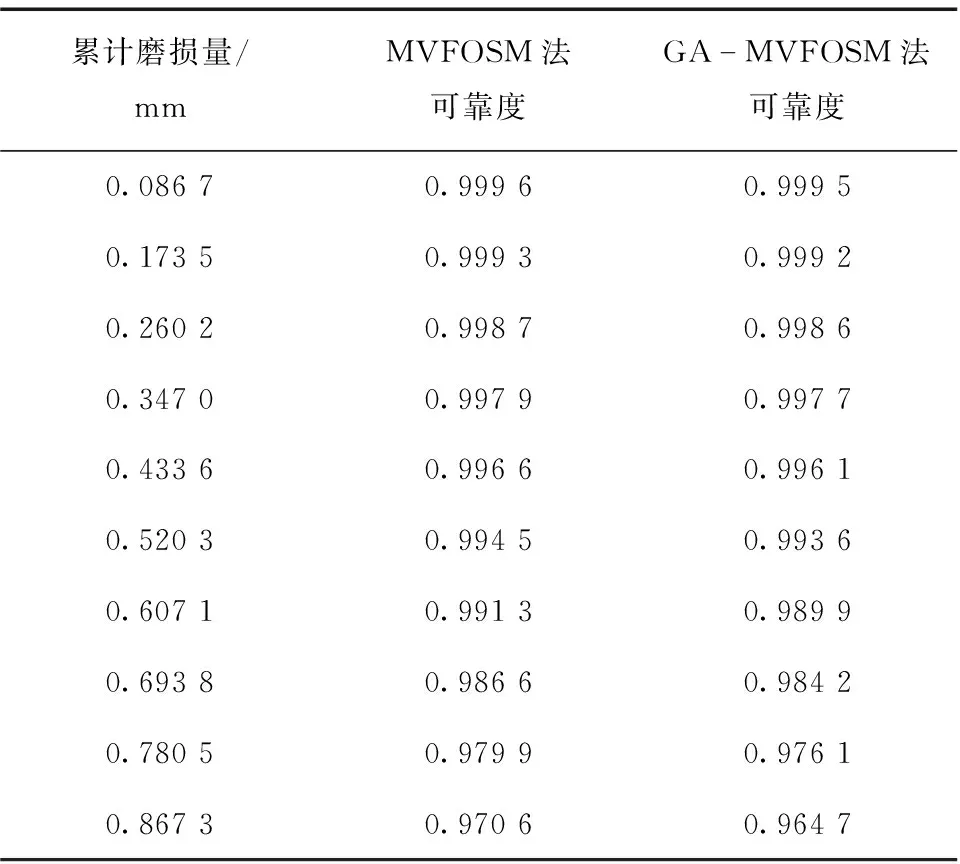
表5 弓头运动可靠度

由表5可知，随着运动副累计磨损量的增加，弓头的运动可靠度逐渐降低，最小值为0.964 7。表明运动副半径的变化影响了受电弓杆件的实际工作长度，由于这种误差的累积，使得受电弓弓头的运动高度逐渐偏离规定高度。弓头运动可靠度对比如图9所示。

图9 2种因素综合的弓头运动可靠度对比

由图9可知，当运动副的总磨损量在0～0.433 6 mm内时，弓头的运动可靠度下降速度较慢；当总磨损量超过0.433 6 mm时，弓头运动可靠度的下降趋势明显加快，说明随着运动副磨损量的增加，受电弓杆件实际工作长度的不确定性对弓头运动高度的影响越来越大。为更好地比较考虑杆件尺寸不确定性后弓头运动可靠度的变化，将通过GA-MVFOSM法获得的2种情况下的弓头运动可靠度进行对比，如图10所示。

图10 2种情况下弓头运动可靠度对比

由图10可知，当运动副的总磨损量在0～0.347 0 mm内时，2种情况下的弓头运动可靠度下降速度均较为缓慢；当运动副的磨损量超过0.347 0 mm时，2种因素耦合情况下的弓头运动可靠度下降速度要高于仅考虑磨损的情况。原因是当磨损量在0.347 0 mm内时，由于杆件尺寸不确定性造成的弓头运动高度误差超过允许范围的概率较小，弓头的运动可靠度较高；当磨损量超过0.347 0 mm时，受杆件尺寸不确定性的影响，弓头运动高度误差超过允许范围的概率变大，弓头的运动可靠度逐渐下降。因此，在实际制造与维修中，应该严格控制杆件的加工误差；定期检查运动副的磨损量是否超限；按照标准检查弓头是否能运动到指定高度，确保受电弓工作可靠性。

5 结束语

提出了一种GA-MVFOSM法，有效地解决了传统一次二阶矩法在功能函数复杂时线性化失效曲面与原失效曲面偏离较大的问题。

建立了运动副磨损可靠性模型，对受电弓进行运动可靠性分析。研究结果表明：当各运动副的磨损量分别超过0.230 0 mm、0.136 6 mm、0.006 6 mm时，运动副磨损可靠度下降趋势逐渐变快；随着运动副磨损量的增加，弓头的运动可靠度均在0.99之上，处于较高水平。因此，为保证受电弓工作可靠性，在检修中应重点检查运动副磨损量是否超限。

建立了考虑磨损与杆件尺寸不确定性的可靠性模型，探究了2种因素耦合对受电弓运动可靠性的影响。研究结果表明：当总磨损量超过0.347 0 mm时，与考虑磨损相比，2种因素耦合对弓头运动高度的影响不断增大，使其运动可靠度不断下降，最小值为0.964 7。因此，为保证受电弓工作可靠性，在制造中应该严格控制受电弓杆件尺寸的不确定性。