微波引导下的滚筒杀青机内电磁场分布研究

张世功

(贵州理工学院理学院，贵州 贵阳 550003)

0 引言

贵州茶产业规模位居全国前列，但产品品质仍与国内知名茶叶存在一定差距。这主要是因为贵州茶叶加工的产业化程度相对落后，在加工技艺改进上的投入相对有限[1-2]。

杀青是茶叶加工过程中的第一道重要工艺，是茶叶形状和品质形成的关键工序[3-5]。其目的是通过高温抑制茶多酚等的酶促氧化，钝化鲜叶中的氧化酶活性，使茶叶便于下一步成形，是茶叶色、形、味形成的关键步骤。传统的滚筒杀青机对茶叶从外至内进行加热，易造成如黔湄601等品种的肥大茶叶杀不透的问题，严重影响了茶产品的品质。微波可使介质内外同时均匀受热，是一种新型的杀青方式[5-6]。将微波引入滚筒杀青机不但可以改善杀青品质，还可保留滚筒杀青下的特有茶香。但对滚筒杀青机进行改造之前，需根据相关参数对腔内的电磁场和温度场进行仿真分析。

由于电磁波在加热腔内的谐振模态受腔体尺寸和微波频率影响，造成腔内电磁场不均匀，本文基于电磁场Maxwell方程组的理论分析，同时考虑电磁场的热效应，利用商业有限元仿真软件对设计腔体的内部电磁场和加热功率场进行数值仿真，研究结论可为微波滚筒杀青机工程改造项目提供技术支撑。

1 理论基础

微波是一种电磁波，电场可使极性分子(如水)以电磁波的频率(约2.4 GHz)高速转动，分子之间形成快速摩擦生热，从而实现对茶叶深层的水分进行快速加热的目的。电磁波的传播与分布特性可用Maxwell 方程组进行描述[7]：

·D=ρ

(1)

(2)

(3)

(4)

D和E分别为电位移和电场强度；ρ为空间自由电荷分布密度；B和H分别为磁感应强度和磁场强度；j为空间自由电流密度分布。在介质内部存在极化和磁化现象，引入本构方程D=εE，B=μH进行描述，ε=ε0εr为介电常数，μ=μ0μr为磁导率，εr和μr分别为相对介电常数和相对磁导率。在微波加热腔中没有自由电荷和自由电流，故ρ=0，j=0。在均匀各项同性介质中，式(1)和式(2)可变化为：

ε·E=0

(5)

(6)

对式(6)两边取旋度，并结合式(1)～式(4)可得

(7)

(8)

一般地，可设电磁波为简谐波，即E=E(x,y,z)e-iωt，H=H(x,y,z)e-iωt代入式(8)有

(9)

由于加热腔壁面为金属材料，趋肤深度较小。微波加热研究中可以将金属视为理想导体，金属体内没有电磁波和电流，但表面可有面电荷和面电流，金属边界处的介质空间边界条件(n为法向单位矢量)可简化为

n·B=0n×E=0

(10)

2 谐振腔中的电磁波传播模式

式(9)和式(10)构成在谐振腔内的电磁波分布及边值问题，在宽、长、高分别为W、D、H的矩形腔中求解该边值问题，得到谐振腔中可以存在的电磁波谐振频率f为

(11)

m、n、p为正整数，每组(m,n,p)的值决定一种谐振模式，E波记为Emnp，H波记为Hmnp，脚标(m,n,p)可取多种组合满足式(11)，不同的谐振模式对应的电磁场分布，即Emnp和Hmnp是简并的。另外，针对某个方向的横电波TE模式可能是另外一个方向的TM模式。对于TE模式，p≠0，对横磁波TM，p可为0，但m，n不能为0，因此(m,n,p)3个数字最多只能有1个为0。谐振腔内最低的振荡频率为3种最低模态对应的频率。谐振腔内每种谐振模式对应于腔内的1种驻波存在形式。微波频率为2.45 GHz时，当W×D×H越大，(m，n，p)的组合方式就越多，谐振腔内包含的振荡模式就越多，电磁场分布就更加均匀，加热均匀性就越好。

但在辐射能量一定的情况下，谐振腔尺寸越大，箱体内的能量密度就越小，加热速度相应减慢。所以谐振腔的尺寸设计需综合考虑以上两方面的问题进行合理设计，根据滚筒杀青机尺寸将谐振腔尺寸设定为500 mm×1 000 mm×240 mm(W×D×H)。若将微波器件置于一排，则箱体长度方向上可根据需要进行延长，仿真中暂定其长度为1 000 mm。

谐振腔在加热时，由于电子器件发热等的影响，电子管输出频率有±0.03 GHz的波动，所以电磁波频率范围为2.42～2.48 GHz，对应波长范围为121～124 mm。

260.28≤4m2+n2+17.36p2≤273.35

(12)

解不等式(12)得到(m,n,p)的组合，即可得到相应的21组模态及相应频率，具体数值如表1所示。

由表1可知，设计的谐振腔内可存在21种谐振模式，对其中的电磁场分布进行仿真计算，选择适合的模态进行机械设计，可提高腔内电磁场和温度场的均匀度。

表1 谐振腔中微波谐振模式和频率

电磁能在介质中转变为热能[8]，其功率流通过坡印廷矢量计算得到：

(13)

P为功率流；s为面积微元；H*为磁场强度的共轭；Re表示取复数实部。考虑到介质因素，平均加热功率最终可写为

(14)

脚标rms表示有效值。另外，根据受热介质的比热容Cp、密度ρ等可得到温度T的上升率为

(15)

最终得到加热功率及温度场。

3 仿真计算

磁控管是产生微波的电真空器件[8]，实质上为置于恒定磁场中的二极管。管内电子受相互垂直的恒定磁场和电场控制，然后与高频电磁场发生相互作用，把从恒定电场中获得的能量转变成微波能量，从而达到输出微波的目的。磁控管产生的电磁能通过磁控管上的天线辐射出来，并经由微波传输系统传入到微波谐振腔中[9-11]。在进行腔体内微波分布分析时，假定微波是从腔壁面的某个区域辐射进入加热腔的。

根据上文所述谐振腔尺寸构建仿真计算模型，对腔内电磁场进行仿真计算，得到相关模式的电磁场分布。图1为表1中序号为18的谐振模式，即 (7,2,2)谐振模式下腔内的电磁场及加热功率分布图。其中，电磁场分布主要集中在中心长轴位置，但谐振腔表面的加热功率也较强。这样的谐振模式容易对电路及设备造成不利影响，是应该避免的情况。

图1 谐振模式(7,2,2)的电磁场及加热功率分布

图2为19号模式，即(7,7,1)情况下腔内的电磁场及受热功率分布图。从图2中波峰分布可明显看出3个方向上的7、7、1个驻波模式，腔内电磁场与加热功率分布相对均匀，且加热功率在腔体表面分布较小，内部场值较大且相对均匀，是较为理想的谐振模型。

图2 谐振模式(7,7,1)的电磁场及加热功率分布

图3为谐振模式(5,12,1)的电磁场及加热功率分布，其与谐振模式(7,7,1)相比，电磁场和热功率要相对更加均匀，但腔体表面热功率比模式(7,7,1)略强。这3种模式比较具有代表性，其他各种模式的电磁场分布不再列出。

由上述分析可知，若要在谐振腔内形成较为均匀的电磁场和温度场，需选择较为合适的谐振模式。首先，腔内电磁场分布要均匀，一般地，模式越大，电磁场分布越均匀；其次，为保护器件，受热功率在谐振腔的表面应尽量小；再次，腔体尺寸严重影响谐振模式，应根据谐振模式设计谐振腔尺寸。对于受热体积小且位置固定的情况(比如微波炉内加热馒头)，可采取小模态[12]，如(1,0,1)进行，只能对腔内中心位置形成快速高效的加热效果。但对于体积小但位置分散且快速移动的受热介质(如滚筒杀青机快速滚动的茶叶)，应采取大模态方式加热，考虑到受热介质反射等对谐振模式的影响，更易形成均匀的电磁场。

图3 谐振模式(5,12,1)的电磁场及加热功率分布

4 讨论分析

介质在进行微波加热时，不同位置上的加热功率会受谐振模式影响，为适应工程应用，对加热腔内相关要求下的电磁场分布进行了进一步的仿真计算，结果表明：

a.谐振腔内的模式越多，电磁场的分布就越均匀，谐振腔内的微波(电场强度)分布也就越均匀，但仍应考虑避免将加热功率出现在腔体表面。当谐振腔内有不规则形状的受热介质时，电磁场更均匀，所以应对工程制作的谐振腔尺寸和形状设计耦合口数目及位置，以形成均匀的温度场，实现茶叶杀青的均匀性。

b.单个磁控管微波馈入形成的电磁场分布规律性较强，3个方向的驻波模式较明显，而在工程应用中，为提升腔内加热功率，并使电磁场更加均匀化，可适当增设磁控管数目。进一步的仿真计算结果表明，微波馈入口位置应尽量不规则排列，图4为4个不同位置馈入(白色方框)情况下某高度的电磁场分布，这样不但加强了腔内加热功率，还可使电磁场的分布更加均匀。

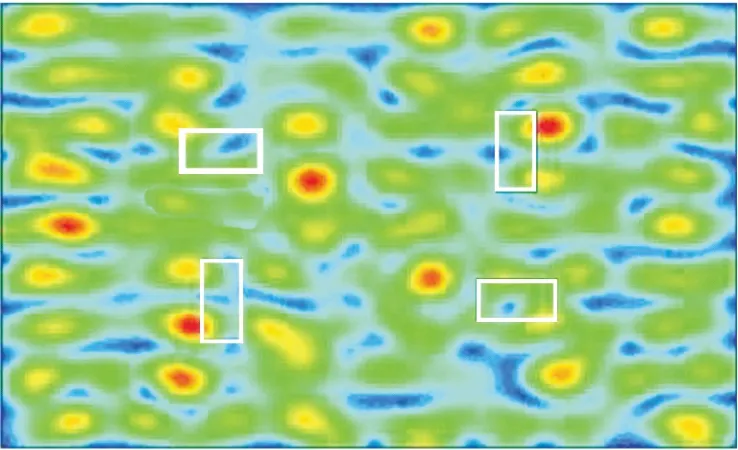
图4 4个微波馈入口某种谐振模态下的电磁场平面分布

c.当谐振腔内有受热物体时，它的介质参数及均匀性会部分改变电场的分布，同时，相关参数受温度、频率等影响，会造成仿真得到的场分布结果与实验有一定差别。

5 结束语

本文在分析微波传播的理论基础上，研究了特定尺寸加热腔内电磁波谐振模式并进行了数值仿真。结果表明：不同尺寸的加热腔存在不同的谐振模式，为达到均匀加热并提高杀青效率的目的，加热腔应通过先期数值仿真进行设计，选择腔内电磁场均匀，且功率场尽量不分布在腔体表面的相关模式进行机械设计。除谐振腔尺寸影响外，微波馈入口位置、方向、数目均对电磁场均匀性有影响。仿真研究结果也可为工程样机设计提供技术方案。