事件触发机制下二阶多智能体系统量化追踪控制

徐光辉，余蒙，付波，赵熙临，陈洁

(1. 湖北工业大学 电气与电子工程学院，湖北 武汉 430068；2. 湖北工业大学 太阳能高效利用与储能系统运行控制湖北省重点实验室，湖北 武汉 430068；3. 湖北工业大学 理学院，湖北 武汉 430068)

近些年，多智能体系统(MAS)的协同控制在工程领域引起了众多研究者的注意[1-5]，例如无人机编队飞行、军事导弹防空部署和快递分拣的移动机器人.刘晨等[6]研究了系统的最优主从一致性控制问题，设计了一种自适应事件触发的控制算法.王誉达等[7]分析了MAS遭受网络攻击的一致性问题，设计了有关网络攻击的控制协议.在实际的工程应用中，为了降低网络资源的消耗，需要设计相宜的控制方法.事件触发机制由此被提出.在事件触发机制下，当智能体的测量误差满足触发条件时，控制器才会再次更新，从而使得控制器的更新频率明显减少.

近些年，基于事件触发的二阶MAS的追踪控制问题引起了众多学者的广泛关注[8-12].Li等[13]分析了在事件触发机制下二阶MAS的追踪控制问题.Fan等[14]提出了一种改进的事件触发控制算法.在数据通信传输中，信息量化可以减少对网络通信对带宽的需求，但是也会影响系统的稳定性.因此，分析MAS在量化环境下的追踪控制问题很有研究意义[15-18].盖彦荣等[19]考虑了在有向拓扑下高阶离散MAS的量化一致性问题.朱韵茹[20]分析了在连续时间一致性协议下的信息量化对二阶异质MAS稳定性的影响.周慧芹[21]为了寻找MAS稳定的最优解，设计了基于量化的一致性控制算法，并且分析了量化误差对系统收敛性的影响.

综合上述讨论，本文引入改进事件触发机制[14]和均匀量化方式[22]，以二阶线性MAS为研究对象[23]，设计了基于事件触发的二阶线性MAS的量化跟踪控制算法，研究其分布式事件触发机制[24].

1 预备知识及问题描述

1.1 代数图论

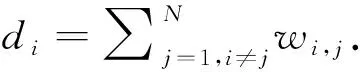
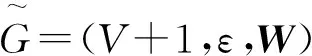
文中考虑比较常见的均匀量化器[25-26]，定义qu:R→αR为均匀量化，则均匀量化qu定义为

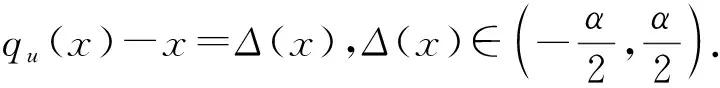
1.2 系统描述

给定一个包含N个跟随者和一个领导者的N+1个智能体MAS，其二阶线性动态方程分别为

(1)

(2)

式(1)，(2)中：xi(t),vi(t),ui(t)∈Rm分别表示跟随者i在时刻t的位置状态、速度状态和控制输入；而x0(t),v0(t)∈Rm分别表示领导者0在时刻t的位置状态和速度状态.

2 主要结果及其证明

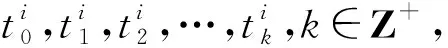
(3)

令ζi(t)=xi(t)-x0(t)，μi(t)=vi(t)-v0(t)，i=1,2，…,N，则定义状态误差为

(4)

给出如下几个定义，即

智能体i的事件触发函数fi(t)设计为

fi(t)=(bi+di)‖ex，i(t)+ev，i(t)‖+‖Wi‖‖ex，i，j(t)+ev，i，j(t)‖-ρiEi(t).

(5)

根据上述的均匀量化性质qu(x)-x=Δ(x)及式(4)，可得控制协议的紧凑形式为

u(t)=-(γ1(L+B)⊗IN)(ζ(t)+μ(t))-(γ1(L+B)⊗IN)(Δx(t)+Δv(t))-

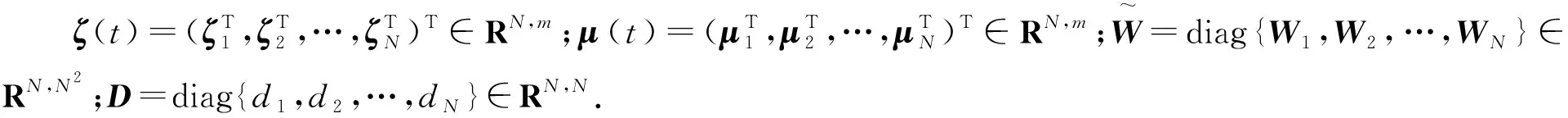
在控制协议(3)和事件触发函数(5)作用下分析MAS(1)，(2)的收敛性，则系统(1)，(2)可改为

(6)

{x(t)‖x(t)-x0(t)IN‖≤ψ/[γ1λmin((L+LT)/2+B)-2θ]}，

{vi(t)‖v(t)-v0(t)IN‖≤ψ/[λmin[γ1(L+LT)/2+B-IN]-2θ]}.

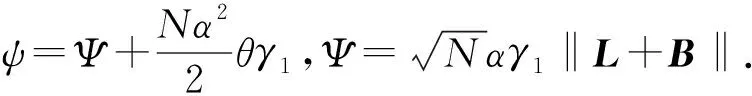
证明：令z(t)=(ζT(t),μT(t))T，构造Lyapunov函数为

(7)

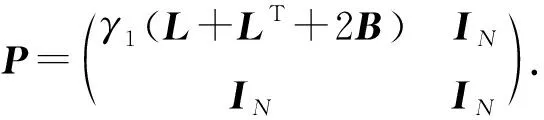
对式(7)求导，再将式(6)代入，可得

(ζT(t)+μT(t))[γ1Π(t)+(γ1(L+B)⊗IN)(Δx(t)+Δv(t))].

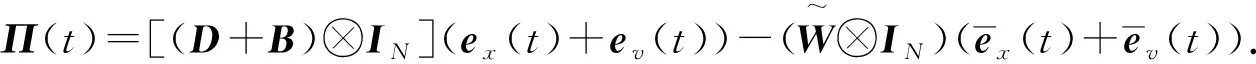
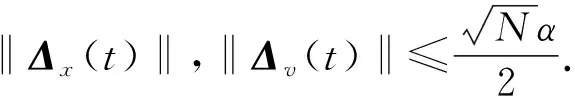
(8)

根据事件触发函数(5)的定义，有

(bi+di)‖ex，i(t)+ev，i(t)‖≤σi，1ρiEi(t)， ‖Wi‖‖ex，i，j(t)+ev，i，j(t)‖≤σi，2ρiEi(t).

其中：σi，1,σi，2>0，并且满足σi，1+σi，2=1.

根据范数性质，‖x-y‖2≤2(x2+y2)，x,y∈Rn，可以得到

因此有

3)将原有的药剂塑料管改为钢管，减弱草酸、TL-1和P86对管道的腐蚀作用，在配制TL-1的搅拌桶上加装盖板，防止蒸汽和粉尘对人体的危害。

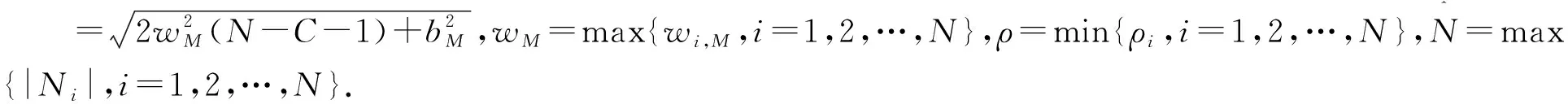
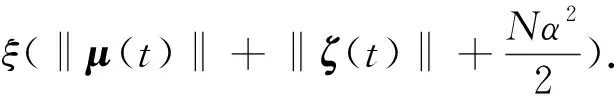
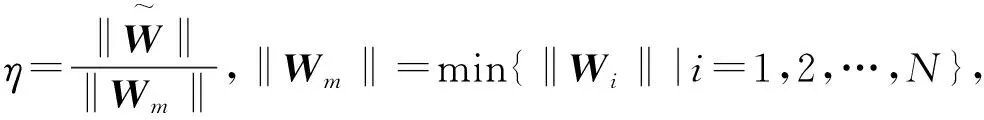
其中：θ=sρϑ，从而可得到

由式(8)和上述证明可得

当γ1>2θ{λmin[γ1((L+LT)/2+B)-IN]}，可以得到所有跟随者的位置和速度分别收敛为

{x(t)‖|x(t)-x0(t)|IN‖≤ψ/[γ1λmin((L+LT)/2+B)-2θ]}，

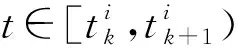
3 仿真实验与分析

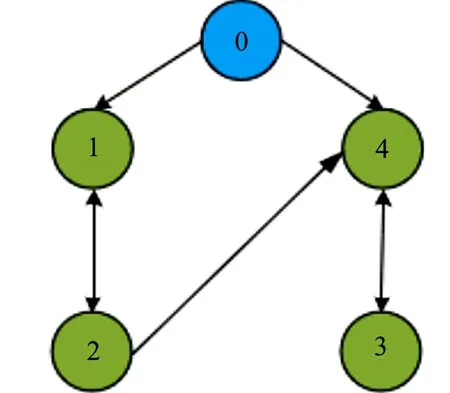
图1 通信拓扑图Fig.1 Communication topology diagram

(a) 跟随者 (b) 领导者图2 跟随者与领导者的位置差轨迹图Fig.2 Position difference trajectory of followers and leader

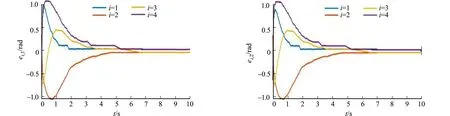
(a) 跟随者 (b) 领导者图3 跟随者与领导者的速度差轨迹图Fig.3 Tracking diagram of speed difference between followers and leaders

图4 事件触发时间序列图Fig.4 Time sequence diagram ofevent-triggered

4 结束语

文中研究了基于事件触发的二阶线性MAS的量化追踪问题，设计了基于事件触发的追踪控制算法.事件触发机制与均匀量化器有关，其中所有的跟随者的状态信息都先进行均匀量化处理，然后再进行信息交互的.基于构建的合适Lyapunov函数，分析得到了与控制增益参数和量化参数有关的系统稳定的充分条件.最后，通过仿真实例验证了理论结果的可行性和有效性.