结合时间序列分解和神经网络的河流溶解氧预测
2020-10-09卢毅敏张红
卢毅敏,张红
(1. 福州大学 空间数据挖掘与信息共享教育部重点实验室,福建 福州 350108;2. 福州大学 地理空间信息技术国家地方联合工程研究中心,福建 福州 350108;3. 数字中国研究院(福建),福建 福州 350003)
河流中的溶解氧(DO)是反映水质状况及自净能力的重要指标[1].高质量浓度溶解氧有利于降解河流中各类污染物,并有效控制底泥释放氮、磷和有机物,当河流复氧速度远低于耗氧速度时,低质量浓度溶解氧将导致需氧生物死亡及水质恶化[2].因此,针对河流溶解氧预测的研究具有重要意义,为水质管理和污染预警提供决策支持.
基于机理模型的河流溶解氧预测方法需要大量的基础资料作为支撑[3],而小流域资料贫乏,随着机器学习与智能传感器技术的快速发展,基于数据驱动的非机理组合预测模型逐渐兴起[4-7].但河流的动态性、不确定性,以及繁杂性使得河流溶解氧随着时间随机变化,呈现非线性、非平稳性特征[8],预测精度难以提高.文献 [9-10]采用小波分解法进行平稳化处理及降噪,并取得较好的预测效果,但这些方法未对DO序列的不同时频特征进行深入挖掘,并且小波基函数依赖于人为选择,给预测结果带来一定主观影响.经验模态分解(EMD)法很好地解决了这个问题[11],仅根据数据自身极值特点进行分解,而具有自适应噪声的完整集成经验模态分解(CEEMDAN)法解决了EMD模态混叠问题[12],以及集合经验模态分解(EEMD)存在大量集成平均计算次数的问题[13].因此,本文提出一种结合CEEMDAN分解和Elman动态神经网络的河流溶解氧预测模型.
1 研究方法
1.1 CEEMDAN分解法
DO时序数据具有明显的非线性和非平稳性特征,任一时间可具有多种波动模式,为了提取DO时序数据潜在的变化特性、周期特征,以及长期趋势,实现对DO序列时频特征的充分挖掘、平稳化处理及降噪,引入CEEMDAN分解法,使噪声残留引起的重构误差在分解阶段叠加抵消.
进行I次实验,通过对每次分解后的余量序列添加白噪声,并进行EMD分解,可得第k个模态分量IMFk(t)及第k个余量Rk(t)为
(1)
Rk(t)=rk-1(t)-IMFk(t).
(2)
式(1),(2)中:I为500;εk-1取值为ε0[std((rk-1(t))/std(Ek-1(wi(t)))],ε0取0.2,std(·)为标准差算子,能使每个分解过程具有适当的信噪比;E(·)为分解算子.
当余量序列Rk(t)的极值点个数小于2时,结束分解,共得到k个代表DO序列不同时频特征的模态分量,以及代表DO序列长期趋势的最终余量R(t).原始DO时序数据S(t)可表示为

(3)
1.2 样本熵
若对分解后的每个DO时频特征都进行建模,会带来预测误差累积;若仅根据频率特征将各特征重组为高频、中频、低频3组,会丢失部分隐含的DO时序变化信息.样本熵(SE)是通过计算时间序列的复杂度来衡量信号产生新模式的概率,抗噪能力强,采用较少的数据段即可得到稳定的熵值,可充分挖掘水环境系统复杂性[14].因此,文中以SE衡量DO各时频特征的自相似性,熵值越大,时频特征越复杂,特征序列的自相似性越小,所包含的特征信息与变化细节越重要,对DO预测结果影响越大,建模时越应当保留.将各DO时频特征依序分别组成维数为m和m+1的向量序列Sm={s1,s2,…,st-m}和Sm+1={s1,s2,…,st-m},其中,si={ui,ui+1,…,ui+m-1}(i=1,2,…,t-m)为IMFk(t)中第i个数据开始,连续m+1个数据组成的向量,m取4.
样本熵定义为
(4)
各时频特征的样本熵值计算式为
(5)
式(4),(5)中:r取0.1~0.2std(IMFk(t))具有较合理的统计特性,文中取0.15std(IMFk(t));Bm(r),Bm+1(r)分别为向量Sj与模板向量Si的匹配概率.
将熵值近似的分量进行合并,得到n个新的重组序列Xt={x1,x2,…,xt}(t=1,2,…,T).
1.3 CS优化的Elman神经网络
DO时序数据具有延续性及自相关性,历史时序数据对未来指标值的变化具有很大影响.Elman动态神经网络作为时间序列预测模型的一种,承接层可以记忆一定程度的DO历史数据,并与当前时刻DO值共同成为隐含层的当前输入.这可以表达历史DO数据与未来DO数据间的时间延迟,捕捉DO数据的时间变化特征,具有适应时变特性的能力[15-17].新兴的布谷鸟搜索(CS)算法只有两个参数(待优化的初始权值与阈值组数n=25,新解的概率p=0.25),通用性好,搜索速率快,不易陷入局部最小值,能有效克服神经网络存在的问题[18-19],并消除预测过程中随机因素的干扰,提高预测精度.将误差值定义为适应度值fit,依据莱维(Levy)飞行原理寻找新解,采用偏好随机游动法替换该解,即
(6)
式(6)中:α>0为步长缩放因子;⊗为逐点乘积运算;levy(λ)为随机搜索路径,可以产生随机步长;R为(0,1)的随机数;xt,p,xt,q表示t代的两个随机解.最终得到最小适应度值fitmin及最优解xbest.
1.4 组合预测模型的构建
基于CEEMDAN分解、SE和CS-Elman动态神经网络构建的河流溶解氧预测方法流程图,如图1所示.首先,使用CEEMDAN方法分解原始DO时序数据,实现对非线性、非平稳性DO序列的平稳化处理及降噪,充分挖掘DO时序信号中不同时间尺度的特征信息及噪声,提取DO时序随时间变化的波
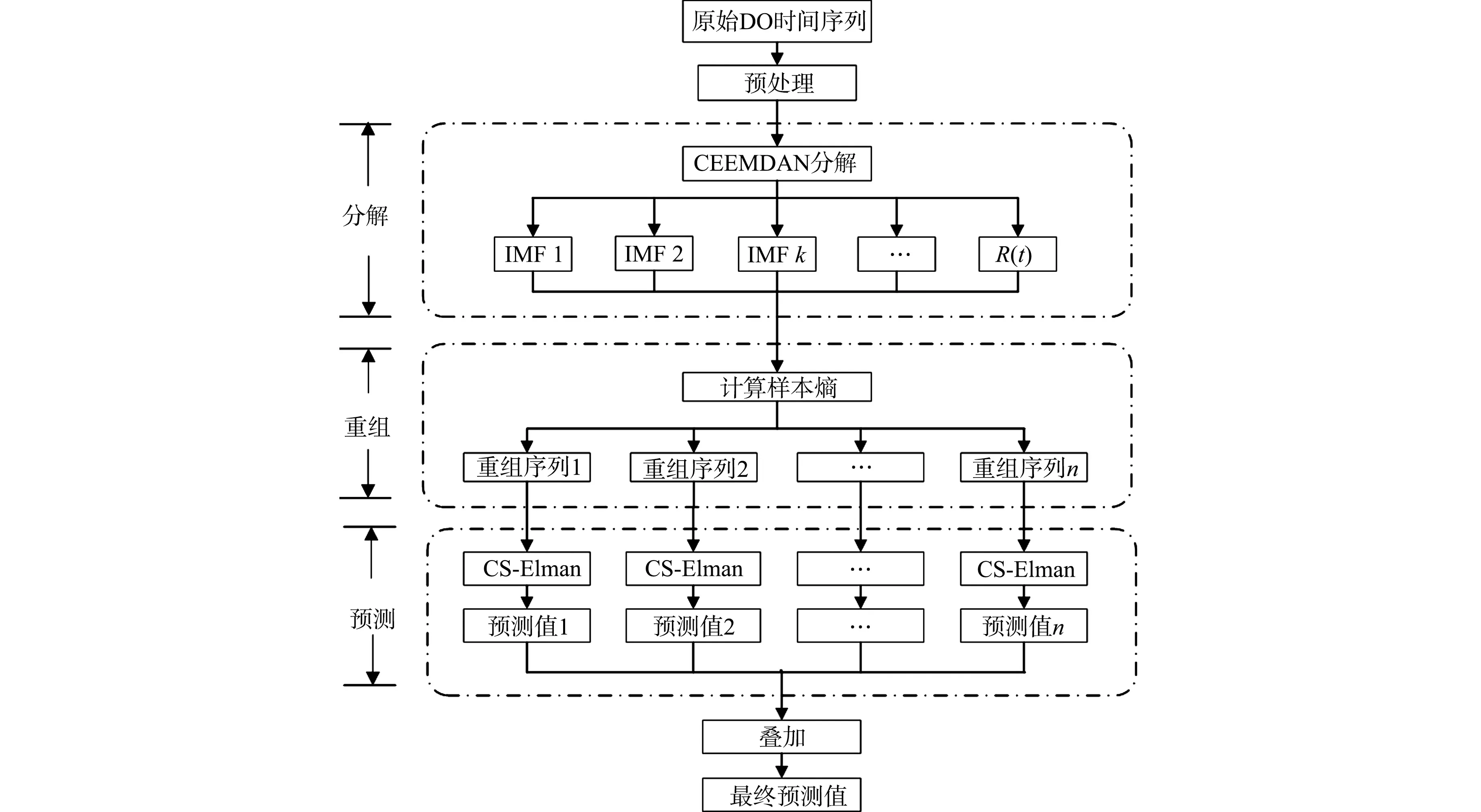
图1 河流溶解氧预测方法流程图Fig.1 Flow chart of dissolved oxygen prediction in rivers
动特征、周期特征及长期趋势.然后,通过计算样本熵值衡量各时频特征的自相似性,将熵值近似的特征重新组合为新序列,以减小计算量和误差累积.同时,保留对DO预测结果具有重要影响的特征信息与变化细节.最后,对新序列分别构建CS优化的Elman预测模型,将预测值叠加,得到最终预测结果.
2 实验分析
2.1 数据预处理
以福建省的晋江流域为研究区域,该流域位于北纬24°49′36″~25°35′13″,东经117°41′13″~118°41′49″,流域总面积为5 629 km2,河长为182 km,河道平均坡降为1.9%,是福建省第3大河流,泉州市境内第一大河流,也是福建省经济最发达地区之一.晋江流域水资源是泉州市重要的饮用水源地,其水质优劣与泉州市经济发展和人民生活水平密切相关.
实验数据来源于福建省环保厅地表水质自动监测站点.晋江流域共有泉州石砻、安溪南英和南安秋阳3个地表水质监测站点,选取各站点2017年3月27日至2019年1月2日的DO监测数据作为研究数据.每日自00:00开始监测,每间隔4 h采样一次.由于监测设备故障、网络传输错误等问题,建模前必须对原始DO监测数据进行预处理.首先,依据GB 3838-2002《地表水环境质量标准》和箱线图剔除异常值;其次,考虑到实验数据集缺失值很少,且DO数据一般短时间内波动较小,所以使用中值插补法对缺失值进行插补;最后,计算日均值,分别得到的647条日监测数据构成完整的DO时间序列S(t)={s1,s2,…,st}.
2.2 河流溶解氧质量浓度预测
DO时间序列CEEMDAN分解结果,如图2所示.由图2可知:原始DO时序数据表现出明显的随机性和非线性,IMF 1~IMF 3时频特征起伏变化明显,表明DO质量浓度受到随机影响;IMF 4~IMF 8时频特征具有明显的周期特征,可知DO时间序列具有季节性变化;余量时频特征较为平缓,表明DO时间序列的长期趋势,各IMF分量迭代次数逐渐降低至0,重构后相对百分比误差达到10-13数量级,表明DO原始数据得到完全分解.

图2 DO时间序列CEEMDAN分解结果Fig.2 CEEMDAN decomposition results of DO time series
计算各IMF分量样本熵,如表1所示.表1中:Δ为差值.由表1可知:各分量的样本熵值整体表现为递减趋势,说明各分量随着波动频率降低,序列的复杂程度越小,随机性也越小;IMF 1熵值最大,和相邻分量IMF 2的样本熵差值为0.230,在所有相邻样本熵差值中为第2大,说明IMF 1与IMF 2之间的相似性较小,两者所包含的特征信息与变化细节的差异较大,所以IMF 1对DO预测结果影响较大,建模时将IMF 1单独作为一个新的重组序列;IMF 2~IMF 4熵值较大,且IMF 2与IMF 3,IMF 3与IMF 4之间的样本熵差值在所有差值中较大,说明IMF 2~IMF 4所包含的特征信息与变化细节对预测结果均有一定影响,也分别单独作为一个新的重组序列;IMF 5~IMF 7熵值较小,序列的复杂程度较低,且IMF 4与IMF 5之间的样本熵差值在所有差值中最大,IMF 5与IMF 6,IMF 6与IMF 7之间的样本熵差值最小,说明IMF 4与IMF 5所包含的特征信息的相似性很小,不应叠加,而IMF 5~IMF 7这3个分量具有一定的相似性,所以将这3个分量叠加作为一个新的重组序列;同理将余量与IMF 8叠加作为一个新的重组序列.
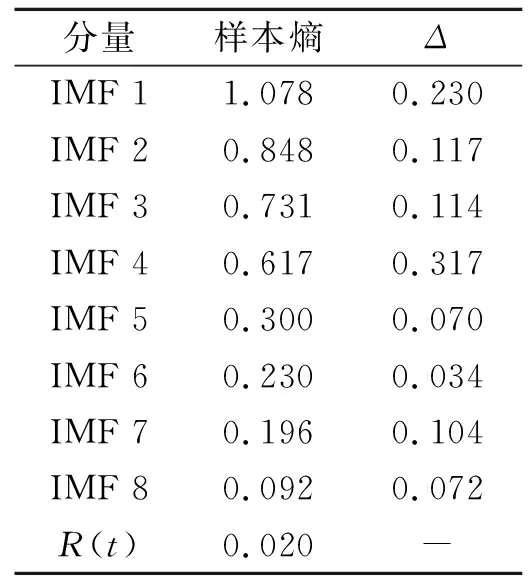
表1 各IMF分量样本熵Tab.1 Sample entropy of each IMF component
根据文献[20]计算各重组序列的平均周期,各重组序列的分量组成及其平均周期结果,各IMF分量重组结果,如表2所示.表2中:T为平均周期.由表2可知:各重组序列的平均周期呈现递增趋势;重组序列1~3为分解出的高频序列部分,平均周期分别为6.55,8.44,12.27 d,表明短期内DO影响因子随机作用引起的DO质量浓度波动情况;重组序列4,5为分解出的中频序列部分,平均周期分别为23.28,51.92 d,表明河流DO质量浓度的月变化、季节性变化;重组序列6为分解出的低频部分,平均周期为337.50 d,表明从长期看,晋江流域DO的周期性是按年度变化的.

表2 各IMF分量重组结果Tab.2 Results of recombined of IMF components
通过计算时间序列的自相关系数确定模型结构,当滞后阶数为N时,时间序列自相关系数较小,可以认为前N-1天的DO质量浓度对第N天的DO质量浓度影响最大,确定Elman模型输入神经元个数为N-1,输出神经元个数为1.对于重组序列Xt,循环将连续N天的数据分为一组,用前N-1天的DO数据预测第N天的DO质量浓度,即前N-1天的DO时序数据作为输入,第N天的数据作为输出,得到样本P={p1,p2,…,pT-N+1},其中,pi=[xi,xi+1,…,xi+N-1]T(i=1,2,…,T-N+1),共T-N组,将前3(T-N+1)/4组作为训练数据,后(T-N+1)/4组作为测试数据.N为3,共得到645组实验数据,将前500组作为模型的训练数据,后145组作为测试数据.
将训练样本P={p1,p2,…,pT-N+1}归一化,并输入CS-Elman模型,将最优初始权值和阈值xbest赋予Elman神经网络,使用误差反向传播和梯度下降法对各个隐含层神经元的权值系数进行修正,直到训练误差小于阈值.为保证模型高效、稳定运行,将Elman神经网络的学习速率设为0.1,训练目标最小误差设为0.000 1,隐含层输出采用激活函数tansig处理,模型训练结束后,将测试样本的DO数据输入到训练好的模型中进行预测,经过线性传递函数purelin处理并反归一化,得到各重组特征序列的预测结果,如图3所示.由图3可知:随着DO数据波动趋于平稳,预测值与实际值越相吻合.
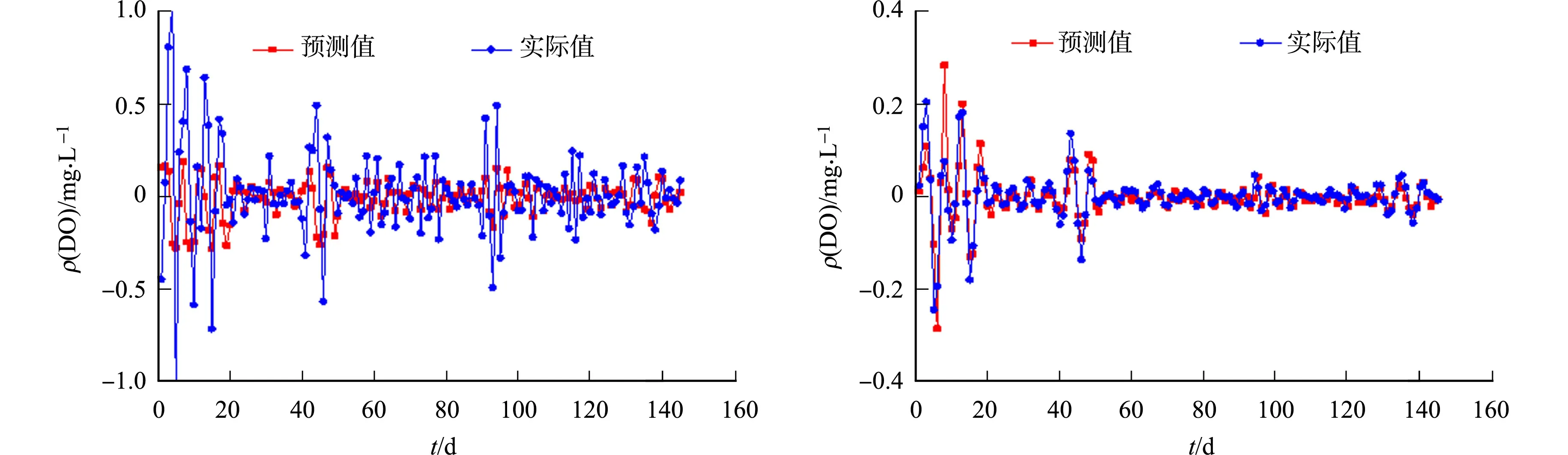
(a) 重组序列1 (b) 重组序列2
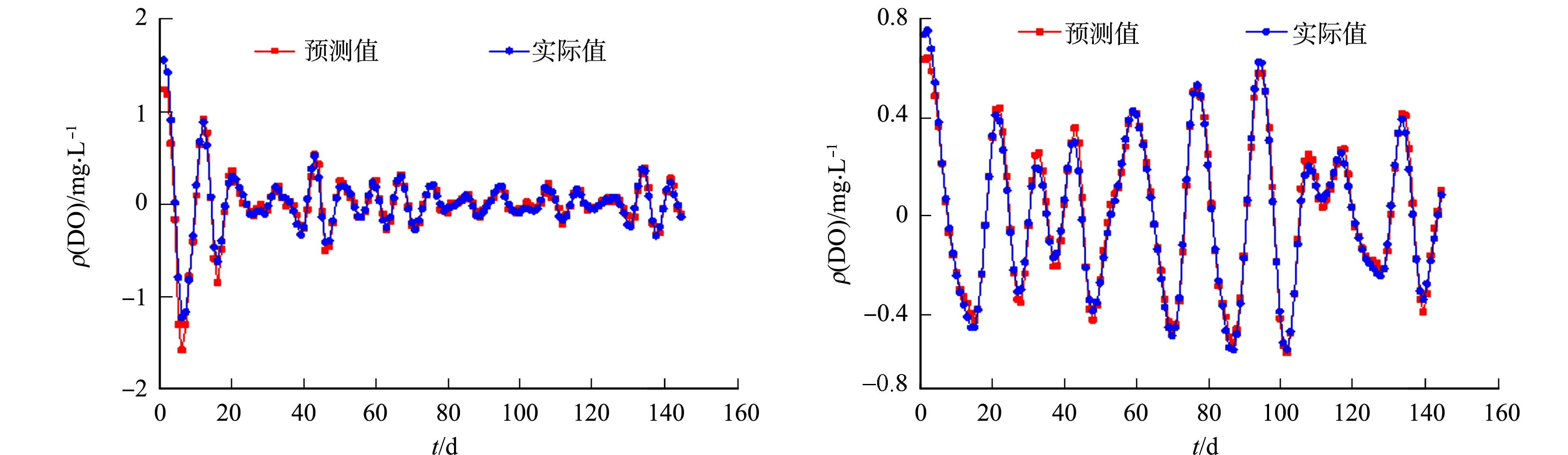
(c) 重组序列3 (d) 重组序列4

(e) 重组序列5 (f) 重组序列6图3 重组序列单步预测结果Fig.3 Single-step prediction results of recombined sequences
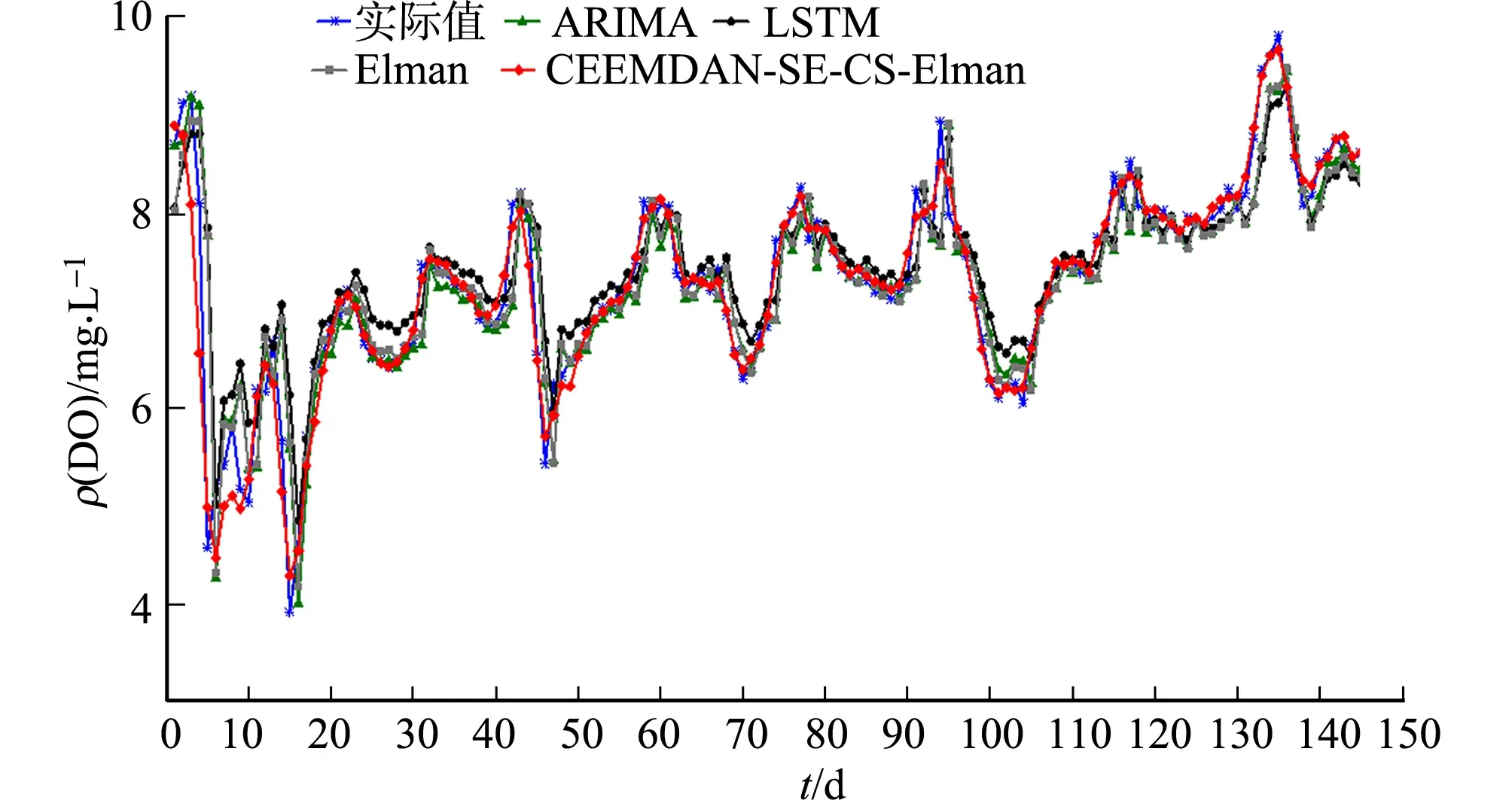
图4 DO时间序列单步预测Fig.4 Single-step prediction of DO time series
2.3 模型对比分析与精度评价
为评估文中模型(CEEMDAN-SE-CS-Elman)的有效性,将其与其他传统时间序列预测模型进行对比,结果如图4所示.由图4可知:文中模型的预测曲线更贴合真实曲线,预测精度更高.
精度评价结果,如表3所示.表3中:EMA为平均绝对误差;EMPA为平均绝对百分误差、ERMS为均方根误差;R2为可决系数.由表3可知:相较于其他经典的时间序列预测模型(LSTM,ARIMA,Elman动态神经网络预测),文中模型的精度更高,更适合作为晋江流域河流溶解氧预测的基准模型;相较于未分解的单一Elman模型,文中模型的EMA提高0.17,EMPA提高2.60%,ERMS提高0.26,R2提高0.197 5,说明采用分解法对溶解氧时序数据进行平稳化处理及降噪,提取溶解氧不同时频特征,能显著提高预测精度,且CEEMDAN分解比EMD,EEMD分解更有效;相较于CEEMDAN-CS-ELman,文中CEEMDAN-SE-CS-Elman模型EMA提高0.04,EMPA提高0.49%,ERMS提高0.05,R2提高0.031 2,说明将样本熵值近似的溶解氧时频特征重组,能减小误差累积,保留重要信息,有效提高河流溶解氧预测精度;与采用遗传算法优化的Elman神经网络模型(CEEMDAN-SE-GA-Elman)进行对比,文中模型EMA提高0.02,EMPA提高0.30%,ERMS提高0.02,R2提高0.016 4,证明CS优化算法的优越性,能进一步提高河流溶解氧预测精度.综合分析,文中构建的模型较其他模型预测效果更好,误差评价指标均为最优.

表3 不同预测模型精度评价
2.4 模型应用结果
为了验证文中模型的实用性,分别对晋江流域安溪南英和南安秋阳站点同期DO时序数据进行预测,预测的结果,如图5所示.由图5可知:预测值与实际值拟合较好,安溪南英站点EMA为0.20,EMPA为2.50%,ERMS为0.31,R2为0.928 1;南安秋阳站点EMA为0.17,EMPA为2.39%,ERMS为0.25,R2为0.902 5.
实验结果表明:文中模型具有一定的实用性,但对于突变数据(如安溪南英站点第133 d),虽能准确预测变化趋势,但存在一定预测误差,在今后的建模中,将针对研究提高突变数据的预测精度,考虑加入其他DO影响因素,使模型更加准确、稳定.
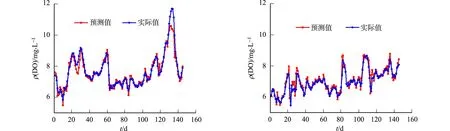
(a) 安溪南英 (b) 南安秋阳图5 不同监测站点的预测结果Fig.5 Prediction results of different monitoring sites
3 结论
针对小流域基础资料少和溶解氧指标值的随机波动性与非平稳性造成预测精度难以提高的问题,提出了基于CEEMDAN分解、样本熵和CS-Elman动态神经网络的组合预测模型.以福建省晋江流域溶解氧数据作为实例验证,得到以下2个结论.
1) 设计CEEMDAN和样本熵相结合的溶解氧时间序列分解方法,实现对溶解氧数据的平稳化处理及降噪,充分挖掘溶解氧数据隐含的不同时间尺度特征,相较传统分解方法,既保留了细节信息,又减小误差累积,有助于解读溶解氧指标随时间变化的内在机理.
2) 对提取的溶解氧时频特征,分别构建Elman动态神经网络模型进行训练和预测,采用全局搜索能力较强的CS算法优化模型,进一步提高了河流溶解氧预测精度.
结果表明,提出的CEEMDAN-SE-CS-Elman模型与其他时间序列预测模型相比,EMA,EMPA,ERMS及R2均有所提高,可为数据驱动的小流域短时河流溶解氧预测提供新方法.
