永磁铁近场等效阻尼计算分析

郭通，李斌，张生坤

（1.中国飞机强度研究所 航空声学与动强度航空科技重点实验室，西安 710065；2.西北工业大学 航空学院，西安 710072；3.中国舰船研究设计中心，武汉 430000）

动力吸振器作为一种可靠性高、耐久性长的被动抑振装置在工程上有大量应用[1-3]。随着技术更新，利用导体在磁场中运动或导体处于时变磁场中受Lorentz 力作用的原理制成的电涡流吸振器，在减振降噪领域开始有一定应用[4-6]。但现有的电涡流吸振器距宽频域、宽速度域应用还有较大距离，原因是目前对电涡流阻尼的定量计算研究并不充分，常用的定性解析法仅在限定条件下具有一定的科学性。解析法是较为传统的一种电涡流阻尼求解方法，该方法将永磁铁视为一圈环形电流， 并应用毕奥- 萨法尔（Biot-Savart）定理积分计算，先得到电磁场强度[7]，再得到导体管相对永磁铁运动所受的Lorentz 力，然后求得电涡流阻尼系数。1999 年，林德华[8]基于毕奥-萨法尔和叠加积分定理直接求得方形永磁铁近场磁场分布，并研究了磁铁尺寸与磁铁表面磁场的分布规律。2004 年，苟晓凡[9]基于分子环流模型和毕奥-萨法尔定理推导了多块磁铁按极性相反排列时的磁场解析表达式。2016 年，李斌[10]等人采用分子环流模型和毕奥-萨法尔定理，并基于准静态假设研究了圆柱形永磁铁的近场磁场分布，推导了其产生的电涡流阻尼力解析表达式。但解析法从准静态理论出发，认为导体运动时产生的感应磁场是均匀分布的，感生的电涡流阻尼力可线性无限增大且和运动频率无关，实际上电涡流互感效应是高度动态的[11]。因此，这种等效阻尼还待进一步明确其动态特性，获取其动态规律。

本研究将直接从时变状态下的Maxwell 方程出发，突破解析法的准静态求解约束，采用有限元方法[12]更全面真实地分析柱塞型电涡流吸振器的动态电磁场分布和等效电涡流阻尼效应，进一步解释主要设计参数对电涡流阻尼的影响规律。

1 等效阻尼系数计算

1.1 解析法

采用环形电流模型，将圆柱形永磁铁等效为一圈导体上的轴对称环形电流， 并应用毕奥-萨法尔（Biot-Savart）定理积分计算出电磁场强度B[13-14]，B 存在Br、Bz两个分量，分别对应径向和轴向。

设导体运动速度为v，由于Bz的矢量方向与v 相同，则Bz不引起涡流效应。因此，圆柱形永磁铁与导体管诱导电涡流之间产生的电磁阻尼力可表示为：

式中：outr 为导体管外半径；inr 为导体管内半径；H 为导体管高度。式（2）中导体管厚度远小于导体管中径，因此，等效电涡流阻尼系数c 为：

式中： mr 为导体管中径； δ 为导体管壁厚度。

1.2 有限元方法

对于一般时变电磁场，Maxwell 方程组的微分形式为[15]：

式中：H 为磁场强度矢量；D 为电位移矢量。

同时，需要电场的连续性方程为：

式中： ρ 为体电荷密度。

要获得一个封闭的系统，仅有Maxwell 方程组还是不够的，还应包括一些描述介质属性的本构方程，它们包括：

式中：M 是磁化强度。已知时变磁场是无散场，故B 可表达为矢量场A 的旋度，即可令：

式中：A 为矢量位。那么，对于时变磁场情形，导体相对磁场以速度v 运动，诱导电流密度可以表示为：

式中：eJ 为除诱导电流之外的外部电流密度，求解时，其默认值为0。联立式（4）—（8），得到包含矢量磁位和标量电位的时变磁场 Maxwell 方程：

针对讨论的电涡流阻尼系数计算问题，所涉及到的介质均为连续的连通介质，因此不考虑电位移D对电磁场方程求解的影响，这样就得到时变磁场下的由矢量磁位表示的Maxwell 方程：

基于COMSOL Multiphysics 可以对永磁铁磁场分布进行有限元求解，并对电流密度和磁场强度积分，求得电涡流阻尼力：

2 电涡流阻尼计算结果分析

本研究利用Bae 等人[16]的磁铁在铜管中自由下落的实验来验证两种算法的准确性。实验如图1 所示，将永磁铁放进足够长的铜管作自由落体运动，铜管上感生环向涡流与磁场相互作用，进而对磁铁产生阻尼力，阻碍磁铁的加速下落。当阻尼力与重力大小相同时，永磁体达到受力平衡状态，将不再向下加速，以平衡速度继续匀速下落至地。

图1 永磁铁自由下落实验原理Fig.1 Schematic diagram of free falling experiment of permanent magnet

表1 为两种算法的结果对比。由表1 可知，有限元方法在电涡流阻尼计算上精度更高，结果更准确。基于此，为进一步明确动态特性对等效阻尼效应的影响，用有限元法分别求解了永磁铁在不同运动速度下的等效阻尼系数，以阐述动态行为对等效电涡流阻尼的影响规律，算例参数见表2。模型采用如图2 所示的二维轴对称形式建立，图2a 中的黑色部分为永磁铁，橙色部分为导体铜管，灰色部分为空气。

相对运动速度设置形式如下式所示：式中：v表示磁铁铜管相对运动速度；v0表示基准速度，取为20 mm/s；n为速度放大倍数。n分别取为1、50、1000、5000，即磁铁与铜管相对运动速度分别为0.02、1、20、100 m/s，分析得到的电涡流阻尼力和阻尼系数见表3。

表1 两种算法结果对比Tab.1 Comparison of results of two algorithms

表2 模型参数Tab.2 Model parameters

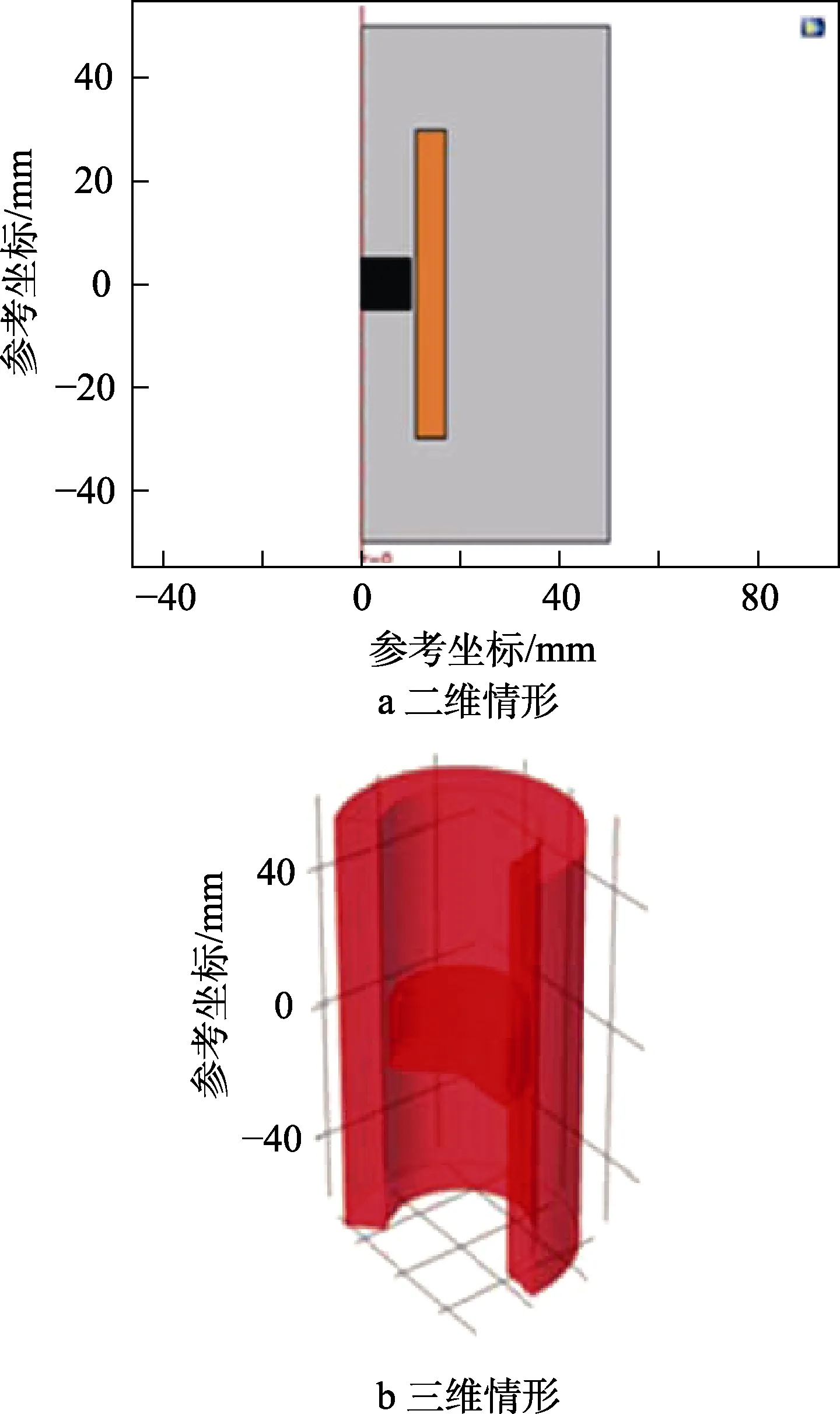
图2 两类求解状态对比模型Fig.2 Comparison model of two kinds of solution states: a)Two dimensional case; b) Three dimensional case

表3 不同速度下的阻尼系数Tab.3 Damping coefficient with different velocity

由表3 可以发现，解析法所得阻尼系数不随相对运动速度变化而变化，时变有限元法求解状态下，阻尼系数会随速度增大而发生变化。低速情况时，时变与解析法结果差异不大，而高速情况时，时变有限元求解结果与准静态的解析法结果差异明显，总体来讲，速度越大偏差越大。

根据式（11）可知，导体在磁场中运动所受的电涡流阻尼力与感生涡流有关。为分析产生上述现象的原因，绘制了不同速度下的磁场分布和铜管中涡流分布情况，如图3 和图4 所示。

图3 为不同速度下的磁场分布情况，图中的线为磁场磁力线。由图3 可知，磁力线随速度变化而变化，而非恒定。低速情况下，磁场磁力线分布基本恒定均匀，而高速情况下，时变磁场磁力线相对低速（或准静态场）发生扭曲，速度越大扭曲越明显。

图3 不同速度放大倍数下的空间磁场Fig.3 Space magnetic field with different velocity magnification

图4 为不同速度下铜管中的涡流场。由图4 可知，铜管中的涡流分布随速度逐渐变化，速度越大，涡流越往铜管内壁集中，这就是电流的趋肤效应[17-18]。对表的参数模型来讲，相对运动速度20 m/s 可视为准静态和时变状态的分界线，在此之前，由于电流趋肤效应较弱，可以忽略电流趋肤效应和涡流对磁场的反项）。在此之后，上述电流的趋肤效应和涡流对磁场的反作用不能忽略，故准静态假设不再成立。

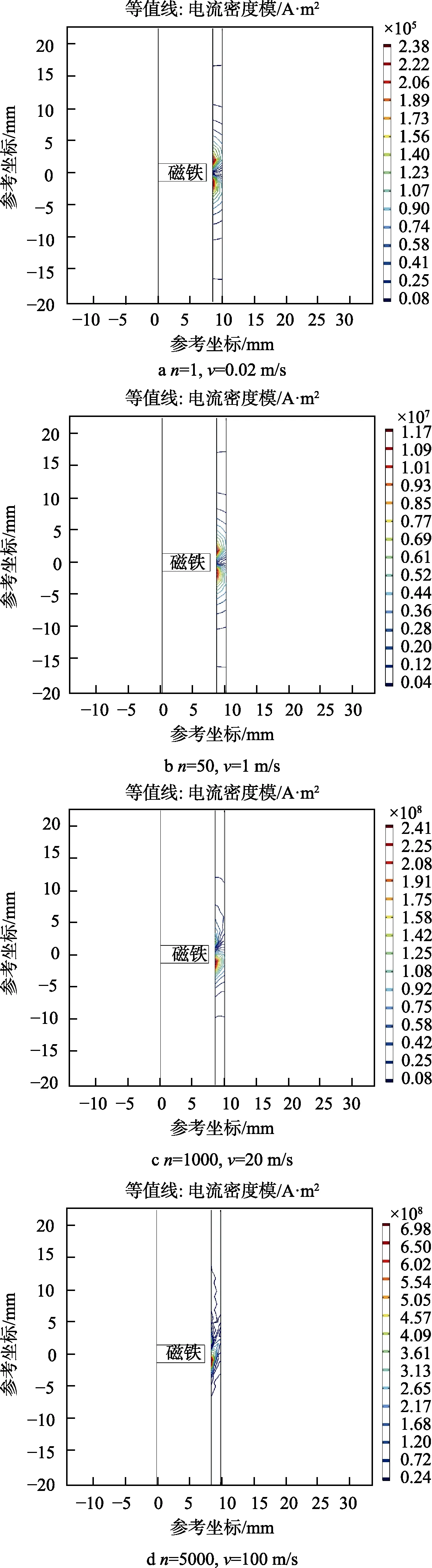
图4 不同速度下铜管中的涡流场Fig.4 Eddy current field in copper tube at different velocity

本研究认为基于时变状态参数求解的有限元法较解析法更为精确和适用，原因概括如下：

1）铜管厚度方向磁场分布的差别：解析方法利用环形电流模型进行永磁铁近场磁场计算时，为简化积分运算，认为磁场沿铜管厚度方向均匀分布，而实际中恒定磁场分布是不存在的，有限元法是基于真实磁场分布求解电涡流阻尼效应，真实度依赖于网格密度，故比解析方法更加精确。

2）铜管厚度方向诱导电涡流分布差别：铜管中诱导电涡流与磁场强度存在线性关系，因此解析方法计算得到的诱导电涡流在铜管厚度方向也是均匀分布的，而时变有限元法的计算结果则是高度依存磁场真实分布，呈非均匀状态。

3 结论

以算例实测值为参考，分别应用解析法和有限元法求解其电涡流阻尼系数。结果证明，与解析法计算结果相比，有限元法与实测值更接近，有更高的准确性。又基于有限元法，研究了相对运动速度和频率对等效电涡流阻尼效应的影响规律，得到如下结论：磁体运动后，由于逐渐增强的电流趋肤效应和涡流对磁场的反作用，磁场磁力线将出现扭曲，磁场强度的变化导致等效电涡流阻尼系数与永磁铁运动速度呈非线性负相关现象。解析法由于基于恒定磁场假设，求得电涡流阻尼系数与实测值误差较大。有限元法基于时变电磁场理论，能反应磁场分布的真实情况，所求得的电涡流阻尼系数与实测值更为接近，计算结果更加精确。