语音信号多维特征参数可视化∗

江军亮 张二华 张丽娜

（南京理工大学计算机科学与工程学院 南京 210094）

1 引言

多维可视化技术是进行数据理解和分析的有效手段，它可以从多维数据中发现隐藏在数据中的现象和规律，并获取有用的信息，帮助用户进行数据理解和分析，为用户进行科学决策提供依据，得到了学者的广泛关注［1］。目前，国内外学者己经提出了多种多维可视化方法，这些方法根据可视化原理的不同可以划分为基于几何的技术、基于降维映射的技术、基于层次的技术、基于图形的技术、面向像素的技术和基于图标的技术等［2］。

多维可视化技术中，需要解决的一个问题是如何进行多维数据的显示，针对这个问题，人们提出了多种方法，例如平行坐标系法［3］、星型坐标系法［4］、散点图矩阵［5］等方法来显示多维数据。在传统的平行坐标可视化方法中，当数据量和数据维度很大时，各种线条交叉重叠在一起会造成视觉上的混乱，用户对高维数据的理解和分析也很困难。人们还提出了多种改进的多维可视化方法［6～7］，但是这些方法可视化效果不理想，仍不能完全满足用户的需求。本文研究了一种新的多维可视化方法来解决现有多维可视化图不直观、不容易定位的问题。

多维可视化的应用很广，可使用多维可视化方法对说话人识别和语音识别的结果进行分析。在说话人识别中，理论上经过端点检测去除无声段后可以提高识别率，但实验表明在有些情况下识别率反而略有下降，本文应用多维可视化方法对识别率下降的原因进行了深入分析。

目前说话人识别大多采用统计模型的方法，在实验中还发现，当使用数字语音训练、用文本语音进行测试时，识别率显著下降，这是由于训练样本与测试样本的分布规律不一致造成的。本文还利用多维可视化方法，直观地说明了在统计模式识别中训练样本与测试样本的分布必须一致，否则将会明显影响识别效果。

2 语音信号多维特征参数可视化的基本原理

2.1 三维数据可视化原理

本文的多维可视化方法基于三维可视化，对于分布在三维空间的体数据来说，有两类不同的可视化算法，面可视化算法和直接体绘制算法［8］。本文主要研究直接体绘制算法，它可以直接由三维数据场通过图像合成生成屏幕上的二维图像，称为体绘制（Volume Rendering）算法，或称为直接体绘制（Direct Volume Rendering）算法［9］。这种算法生成的图像质量高，且具有便于并行处理的优点［10］。

经典的Splatting 算法首先由Westover［11］提出，其原理是先选择重构核，再计算通用足迹表，构造特定视线下的足迹表，然后按层对体数据逐个投影查足迹表获得对屏幕像素的贡献，最后进行图像合成。针对经典Splatting 算法的缺点，Westover 又提出了基于帧缓冲的Splatting 算法［12］，该算法选择数据体可见面中的法向量与视平面法向量夹角最小的面作为投影方向面，然后沿着与该投影方向面垂直的坐标轴进行切片，每个切片内部采样点做加法操作，而切片之间做融合操作。

本文采用的三维可视化算法是基于View-buffer的Splatting算法［13］，基本思想是选择与视平面平行的方向构造View-buffer，当视平面发生变化时，View-buffer 也随之改变，并始终与视平面平行，每个View-buffer 内部的采样点做加法操作，而View-buffer 之间做融合操作。由于View-buffer 始终都是平行于视平面，因此改进的算法不仅能够解决重叠问题，而且还能较好地消除Popping现象。

2.2 多维数据可视化原理

本文提出一种以三维数据可视化为基础的多维数据可视化方法，先通过主成分分析（Principal Component Analysis，PCA）进行降维，用较少的维数表示多维数据的主要信息，然后将每维特征参数离散化，以三维数据可视化为基础，采用逐维展开法，分层次显示。

五维数据可视化原理如图1 所示，五维数据可用x=（x1，x2，x3，x4，x5）来表示，前三维x1，x2，x3构成的小长方体，可以作为三维数据可视化子图，先根据第四维x4值的大小进行横向扩展，再根据第五维x5值的大小进行纵向扩展。每一个小长方体可以使用基于View-buffer的Splatting算法进行绘制。

图1 五维数据可视化原理图

多维数据可视化具体过程为：将三维数据可视化图作为子图，如果是四维数据可视化，则首先将第四维的值离散化，再对三维可视化子图进行横向扩展，可以看作为一行三维数据体。如果是五维数据可视化，则在四维可视化的基础上，将第五维的值进行离散化，并在纵向上扩展。可由三维可视化子图组成的二维阵列来显示五维数据的可视化，五维空间中相邻的点，在三维子图阵列中也是相邻的，并且任一个三维子图都可以进行五维坐标的定位。五维可视化阵列又可以看作更高层次的一个子图，简称五维子图，可由五维可视化子图组成的更高层次的二维阵列来显示七维数据的可视化。七维空间中相邻的点，在五维子图阵列中也是相邻的，并且任一五维子图都可以进行七维坐标的定位。同理，可由七维可视化子图组成的更高层次的二维阵列来显示九维数据的可视化，九维空间中相邻的点，在七维子图阵列中也是相邻的，并且任一七维子图都可以进行九维坐标的定位。以此类推，层层扩展，每一更高层次都扩展2维，可显示11维、13维……数据的可视化。

3 语音信号多维特征可视化的主要步骤

3.1 端点检测

语音信号一般可分为无声段、辅音段、过渡段和浊音段［14］，其中无声段不包含说话人的基音频率和共振峰等个性特征，无声段的混入会明显降低说话人的识别率，准确的端点检测能排除无声段的干扰，提高识别系统的性能。

传统的双门限算法主要依靠短时平均能量和短时平均过零率来进行端点检测。在进行端点检测时，根据三个阈值参数：低能量阈值EL、高能量阈值EH、短时平均过零率阈值ZH进行有声段判决。

本文采用的端点检测算法为多阈值端点检测算法，传统的双门限算法，检测辅音段时，只要短时过零率超过阈值ZH就判断为辅音，忽视了能量的限制，造成部分无声段混入了辅音段，该算法增设辅音能量阈值EC和疑似辅音能量阈值ES［15］，并将过零率修改为跨过正负门限的次数，提高过零率的抗干扰能力，能有效提高端点检测的正确率。多阈值端点检测有声段判断方法如表1所示。

表1 多阈值端点检测有声段判断方法

3.2 Mel频率倒谱系数

Mel 频率倒谱系数（Mel Frequency Cepstrum Coefficient，MFCC）模拟了人耳对语音信号的感知特性，是说话人识别系统中最常用的特征参数［16］。人的听觉系统是一个特别的非线性系统，感知不同频率信号的灵敏度是不同的［17］。Mel 频率与实际频率的对应关系如下：

其中，实际频率f的单位为Hz。

MFCC 参数的求取过程是将原始信号通过一组三角滤波器组，然后转换到倒谱域的过程［18］，其流程如图2所示。

1）原始语音经过预加重、分帧、加窗等预处理得到每一帧的时域信号x（n）。其中预加重的目的去除口唇辐射的影响，增强语音的高频能量，通常选用一阶数字滤波器H（z）=1-uz-1，u 取0.95。由于语音信号具有短时平稳性，为了使帧与帧之间平滑过渡，相邻两帧之间重叠半帧，帧长选择32ms。加窗处理是为了减少频谱分析时产生能量泄漏，一般选用汉明窗，如式（2）所示。

其中，N为窗口长度，n为窗内数据点序号。

图2 MFCC特征参数提取过程

2）将每一帧的时域信号x（n）经过快速傅里叶变换（FFT）得到频谱X（k），如式（3）所示。

3）根据频谱X（k），即振幅谱，用一组三角滤波器进行滤波处理，得到每一个三角滤波器的输出，如式（4）所示。

其中，Yi为第i 个滤波器的输出；Xk为频谱上第k 个频谱点的振幅；Fi为第i个滤波器的中心频率。

4）将每个三角滤波器的输出做对数运算，得到相应频带的对数振幅谱；并进行反离散余弦变换，得到MFCC参数，如式（5）所示。

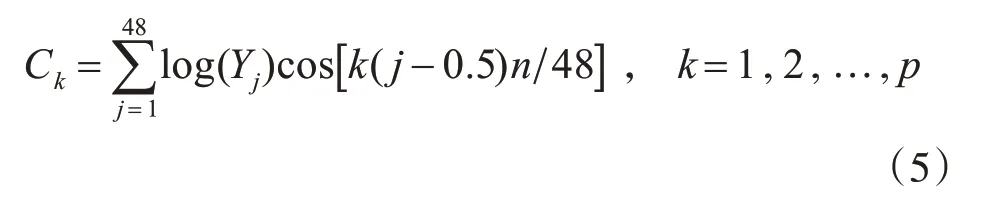
其 中p 为MFCC 参 数 的 阶 数，取12。｛C1，C2，…，Cp｝即为所求的MFCC参数。

3.3 主成分分析

主 成 分 分 析（Principal Component Analysis，PCA）是一种常用降维方法，它可以用较少的维数表示多维数据的主要信息。计算过程如下：

输入：n 维数据集Xm×n，m 为样本个数，n 为每个样本的维数；

输出：k 维数据集Ym×k，m 为样本个数，k 为每个样本的维数。

1）按列计算数据集Xm×n每一维的均值，然后将Xm×n减去每一维的均值得到数据集Am×n；

2）求解矩阵Am×n的协方差矩阵，并将其记为Cn×n；

3）计算协方差矩阵Cn×n的特征值和特征向量Vn×n；

4）将特征值按照从大到小的排序，选择其中最大的k 个，然后将其对应的k 个特征向量分别作为行向量组成特征向量矩阵Wk×n；

5）计算Ym×k=Am×nWTk×n，即将数据集Am×n投影到选取的特征向量上，这样就得到了降维到k 维的数据集Ym×k。

3.4 高斯混合模型

3.4.1 GMM模型

目前，说话人识别方法中常用的方法是高斯混合模型（Gaussian Mixture Model，GMM），本文采用该方法进行实验。GMM 本质上是一个多维概率密度函数，即用多个高斯分布概率密度函数的加权组合来描述特征矢量在概率空间的分布情况［19］，理论上，GMM 可以拟合任意类型的分布。说话人识别中，M阶GMM的概率密度函数如式（6）所示：

其中，x 为K 维的声学特征矢量；λ为GMM 模型的参数集；i为高斯分量的序号；ci为第i个分量的混合权值，且满足c1+c2+…+cM=1；bi（x）为高斯混合分量，一般采用K维单高斯分布函数，如式（7）所示：

其中，μi为均值矢量；∑i为协方差矩阵，i= 1，2，…，M。

GMM 参数集λ可由各混合分量的权值、均值矢量及协方差矩阵组成，如式（8）所示：

3.4.2 GMM模型说话人识别

对于测试语音特征矢量X=｛x1，x2，…，xT｝，GMM 说话人识别过程就是寻找模型λ=｛λ1，λ2，…，λN｝中使得测试样本X 后验概率最大的模型λi*，则λi*对应的说话人i*即为识别结果［20］。根据贝叶斯公式可知，特征矢量X 在模型λi下的后验概率P（λi|X）如式（9）所示：

其中，P（X|λi）为第i 个说话人对特征矢量X 的条件概率；P（X）为全部模型条件下X的概率；P（λi）为识别为第i个人的先验概率，一般情况下，可以认为每个人的先验概率是相等的，如式（10）所示：

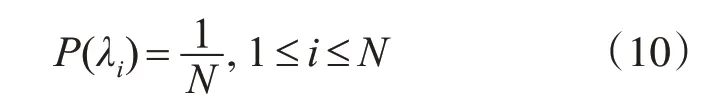
求P（λi|X）的最大值的过程可转换成求P（X|λi）最大值的过程。因此，识别结果可以用式（11）来表示：

其中，i*为识别出的说话人。

3.5 说话人实际散点分布图

实验使用的语音库来自南京理工大学NJUST603 语音库，库中包含423 人的语音，其中男生210 人，编号为M001-M210，女生213 人，编号为F001-F213；每个人有三段阿拉伯数字语音，编号为N1、N2、N3；四段汉语文本语音，编号为T1、T2、T3、T4。采样频率为16kHz，采样精度为16位。

为了对比说话人实际散点分布和理论模型的差别，本文首先显示说话人实际散点分布图，散点图生成过程如下。

1）首先对语音库中说话人编号为F001-F050、编号为M001-M050 共100 人的T4 文本语音提取MFCC 特征参数，对每个说话人的每帧语音数据，用48 个三角滤波器组进行滤波，再取前12 维MFCC特征参数。

2）对步骤1）的12 维MFCC 数据的每一维，按所有说话人特征参数的最大值、最小值进行归一化。将所有100 个说话人的所有训练语音帧的特征参数，对第j维统计总的最小值minj，最大值maxj，将minj映射为0，maxj映射为1，其余值按线性内插，将第j 维特征参数归一化到0～1，再求均值`uj，j=1，2，…，12，均值`uj在做PCA分析时会用到。

3）对步骤2）的所有人的12 维归一化后的数据，进行PCA 分析，取前5 维较大的特征值对应的特征向量作为投影的主轴，将减去每一维均值的12维数据投影到主轴上，从12维降为5维。

4）将步骤3）的数据，即PCA 后的特征值再进行归一化。对每一维，按100人（50个男声、50个女声）的最大值、最小值进行归一化。

5）对步骤4）的数据，进行离散化。对每个说话人，按所有人的每一维的最大值、最小值线性离散化。对第1、2、3 维，进行64 等分；对第4、5 维，进行8等分。

6）对步骤5）的数据，对每个说话人，根据离散化后的语音帧的特征值，绘制5维散点图。

图3 为说话人F020 的语音特征参数离散化后的5 维散点图，其中黑色点为无声帧的特征参数散点，灰色点为有声帧的特征参数散点。从图3 中可以看出无声帧和有声帧的聚集区域是不同的，无声帧的特征和有声帧的特征是有差异的。但在有声帧和无声帧之间的过渡段有少量特征重合的语音帧，这是因为在求取MFCC 特征参数时，转换到对数振幅谱时进行取对数操作，使得有些无声帧的特征值被相对增强，因此有少量的无声帧和有声帧的特征重合。

图3 说话人F020的所有语音帧实际5维散点分布图

3.6 说话人理论模型图

为了直观地显示GMM理论模型在多维空间上的分布特征，本文绘制了说话人GMM 模型训练后的理论概率分布图，理论模型概率分布数据生成过程如下：

1）对3.5节步骤4）的数据（未进行离散化），用GMM 模型进行训练，得到理论模型，得到32 阶、5维、高斯混合模型的混合权系数、各维的均值、方差。

2）根据得到的GMM 模型参数，绘制理论模型的概率分布，对各维特征值进行离散化，第1、2、3维，进行64 等分；对第4、5 维，进行8 等分。各维特征值进行离散化时，与3.5 节步骤5）的区间界限完全一样。计算GMM模型对应各区间的理论概率值（GMM概率密度×5维网格单元的体积）。

3）根据得到的5维理论概率值数据，将概率值的最小值映射为0，最大值映射为255，其余值按线性内插，得到5维的理论模型数据。

将生成的理论模型数据进行5 维可视化，图4为说话人F38 的GMM 理论模型概率分布5 维可视化图。其中黑色的为高概率区域，灰色为低概率区域。

4 实验及结果分析

4.1 端点检测对识别率影响

4.1.1 实验条件

选取文本语音T4 中的50 个男生和50 个女生的语音作为训练语音；分别用端点检测前和端点检测后的语音特征参数训练GMM 模型；GMM 模型的阶数为32 阶；采用12 维的MFCC 经过PCA 提取主要的5 维特征参数训练模型，训练时间为60s；用文本语音T3 进行测试，测试时间分别为4s、8s、…、36s，并分别用端点检测前和端点检测后的语音进行对比，进行说话人识别。

图4 说话人F038的GMM理论模型概率分布5维可视化图

4.1.2 评价标准

说话人识别评价指标为识别率，计算公式为

4.1.3 实验结果及分析

按4.1.1 节的实验条件进行实验，得到的识别率结果如图5所示。

图5 端点检测前后识别率结果对比图

从图5可以看出，当测试时间小于12s时，端点检测后明显高于端点检测前的识别率。当测试时间在16s 左右时，端点检测后比端点检测前的识别率低2%左右。当测试时间高于20s 时，端点检测后的识别率稳定在98%，端点检测前的识别率在96%附近波动。从总体来看，端点检测可以提高说话人识别系统的识别率和稳定性。

应用多维可视化方法来进一步分析上述结果，图6 为说话人M026 端点检测前用所有语音帧的多维特征得到的GMM 模型分布，图7 为说话人M026经过端点检测后用有声帧的多维特征得到的GMM模型分布。图8 为说话人F016 端点检测前所有语音帧实际散点投影到理论模型分布，图9 为说话人F016 端点检测后有声帧实际散点投影到理论模型分布。

图6 说话人M026端点检测前用所有语音帧的多维特征得到的GMM模型分布

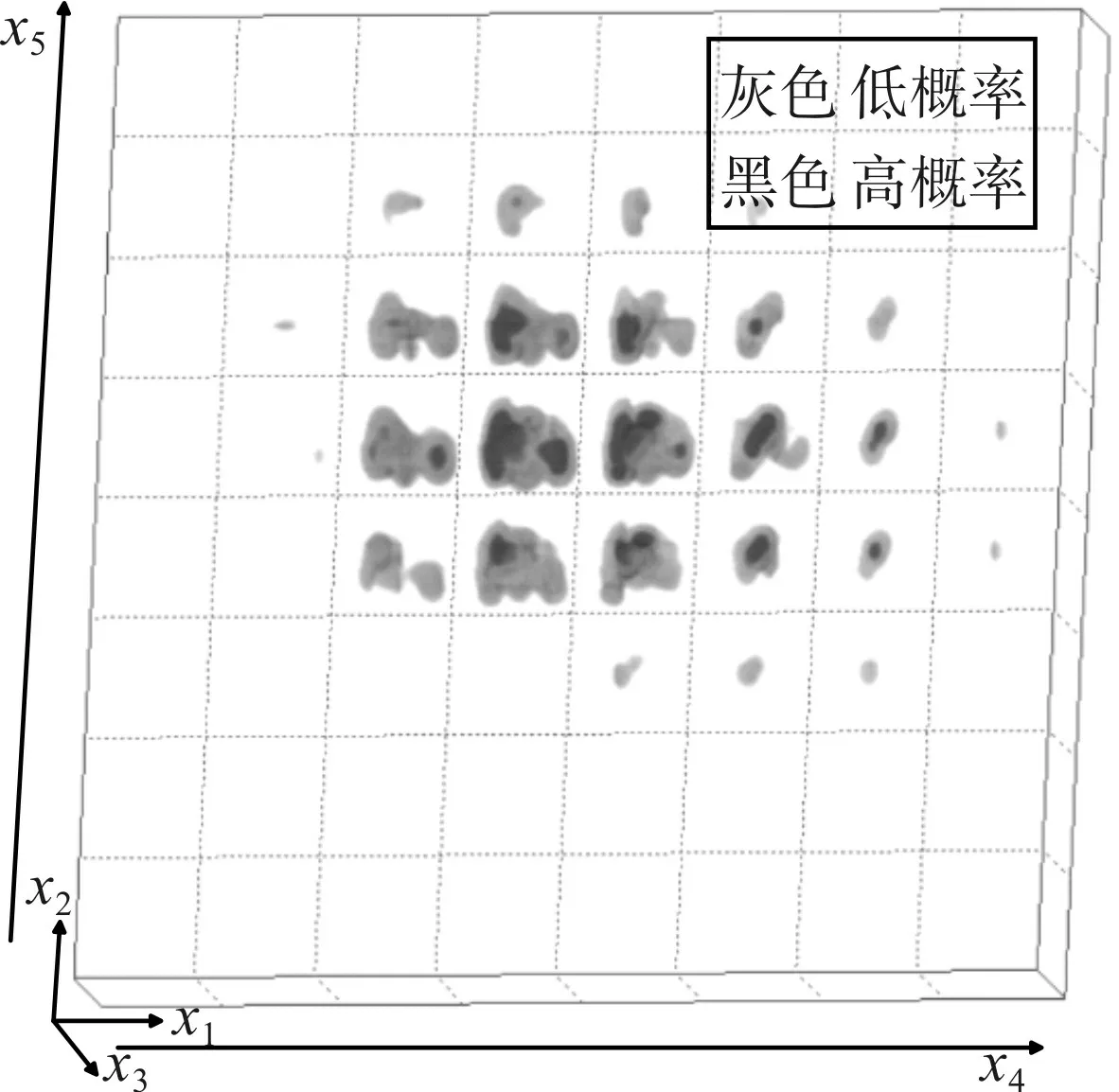
图7 说话人M026经过端点检测后用有声帧的多维特征得到的GMM模型分布

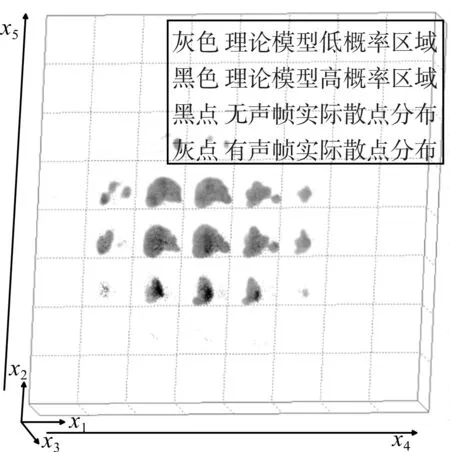
图8 说话人F016端点检测前的所有语音帧实际散点投影到理论模型分布

对比图6 和图7、图8 和图9 可以看出，端点检测后比端点检测前的理论模型分布覆盖范围更大，基本上完全覆盖了训练语音的特征。从图8 可以看出，端点检测前，有少量语音帧不在理论模型范围内，理论模型没有完全覆盖测试语音的特征。从图9 可以看出，端点检测后，有声帧基本都在理论模型的高概率区域，理论模型基本完全覆盖了测试语音的特征。

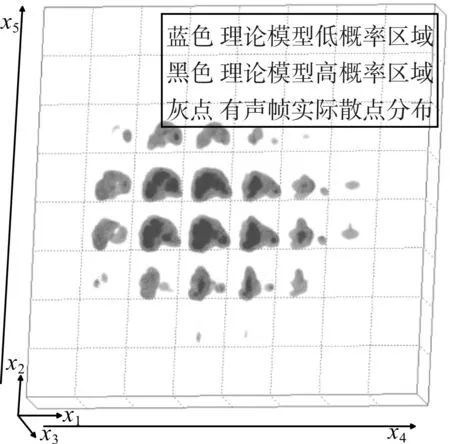
图9 说话人F016端点检测后的有声帧实际散点投影到理论模型分布

4.1.4 说话人识别鲁棒性分析

鲁棒性评价指标可以用得分差来表示：

说话人识别就是对每一帧的特征参数的对数得分进行累加，得分最高的说话人为最后识别结果。得分差越大，说明识别为第一名的概率得分远大于其他说话人的得分，以绝对的优势取得识别结果，抗干扰能力强，识别结果稳定，鲁棒性好。表2为端点检测前后前2 名平均得分差对比及端点检测后平均得分提高百分比。

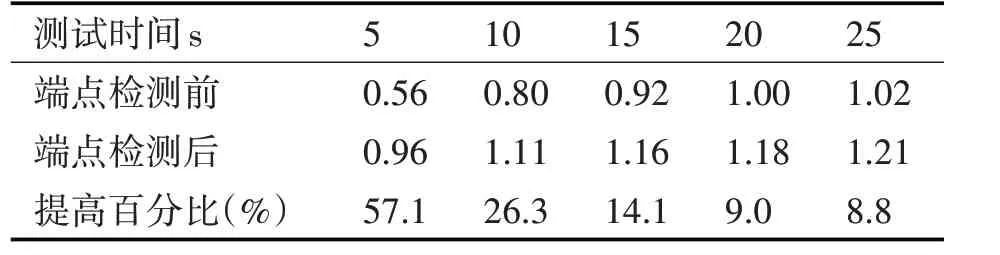
表2 端点检测前后前2名平均得分差及提高百分比

从表2可以看出，当测试时间小于10s时，端点检测后的平均得分差比端点检测前有了明显的提高，端点检测可以明显提高模型的鲁棒性。当测试时间为15s 时，虽然端点检测后识别率略有下降，但是模型的鲁棒性却提高了14.1%。端点检测前，识别结果鲁棒性较差；端点检测后，识别结果鲁棒性好，结果可靠，因此说话人识别中进行端点检测是很有必要的。

4.2 测试语音对识别率影响

4.2.1 实验条件

选取数字语音N3 中的50 个男生和50 个女生的语音作为训练语音；GMM 模型的阶数为32 阶；采用12 维的MFCC 经过PCA 提取主要的5 维特征参数训练模型，训练时间为60s；再分别用文本语音T4、数字语音N2进行说话人识别测试，测试时间分别为5s、10s、…、30s。

4.2.2 实验结果及分析

按4.2.1 节的实验条件进行实验，得到的识别率结果如表3所示。

表3 不同测试语音识别率结果

从表3 可以看出，当使用数字语音N3 训练模型，用数字语音N2 进行测试时，识别率较高；用文本语音T4 进行测试时，识别率较低，这是由于测试样本与训练样本中音素的分布不一致，数字语音中仅包含0-9 的音素，而文本语音中包含了更多的音素，数字语音的模型未完全覆盖文本语音的特征，造成部分未覆盖到的文本语音帧的后验概率很低，明显影响了识别率。

应用多维可视化的方法来进一步分析数字语音训练、文本语音识别时识别率明显降低的原因。图10 为说话人F001 的文本语音T4 理论模型分布图，图11为说话人F001的数字语音N3理论模型分布图，图12为说话人F001的文本语音T4实际散点分布图。

图10 说话人F001的文本语音T4理论模型分布图

图11 说话人F001的数字语音N3理论模型分布图

对比图10 和图11 可以看出，数字语音与文本语音的理论模型分布不一致，数字语音的理论模型分布范围很小，包含的音素较少；而文本语音的理论模型分布范围很大，包含的音素较多。对比图11和图12可以看出，当使用数字语音训练模型、文本语音进行测试时，文本语音的实际散点分布有大部分不在数字语音的理论模型范围内，因此，使用文本语音进行测试时，识别率显著降低。

图12 说话人F001的文本语音T4实际散点分布图

5 结语

本文提出了一种新的多维可视化方法，该方法可以直观地显示多维语音特征参数在多维空间上概率分布情况。应用多维可视化方法分析了说话人识别中经过端点检测后识别率往往略有下降的原因；还直观地说明了在统计模式识别中训练样本与测试样本的分布要保持一致，否则会严重影响识别效果。下一步还将应用该方法研究单个汉字的多维语音特征可视化，分析语音识别发生错误的原因。