T形刚构桥转体施工设计与控制分析

钟栋材 薛 飞 万 波 张瀚文 李文文

(1.中铁二十四局集团新余工程有限公司 江西新余 338009; 2. 中国铁路南昌局集团有限公司 江西南昌 330002;3.福建工程学院 福建福州 350118; 4.南昌铁路勘测设计院有限责任公司 江西南昌 330002)

0 引言

随着城市立体交通建设的不断发展，出现了大量需要跨越既有线路的新建桥梁，为减少对既有线路的干扰，转体施工法作为经济可行的方案得到了广泛应用[1-3]；近年来的诸多学者对转体施工技术开展了大量深入研究[4-5]，使桥梁转体施工技术得到了进一步完善。

转体施工过程中转动体系始终处于不稳定平衡状态，为使转体顺利进行，对桥梁稳定性的控制成为重中之重，目前我国学者对其已积累了大量工程经验。工程实践发现，球铰摩擦力矩的测量对转体施工具有较大影响[6]，国内学者针对球铰摩擦力矩和静摩擦系数计算方法也进行了相关的理论分析，并提出了设计指导建议[7-8]。部分学者还结合工程案例，对比了3种不平衡力矩的测量方法[9]，有的学者甚至还对不同桥型转体施工中关键控制要点进行了总结，对不完善之处提出了改进意见[10-13]；有的学者结合有限元软件对转动体系进行了精细化研究[14]，详细介绍了转体施工关键控制技术要点[15]。虽然转体施工在我国有了一定的发展，但相关理论对设计的指导还不够完善，需要结合实际工程验证理论分析的可行性，并对影响转动体系关键参数进行分析。

基此，本文依托跨越沪昆铁路、蒙华铁路联络线的新余市环城立交桥梁工程，针对大吨位T形刚构桥转体施工的转体设计需求，对T形刚构桥平转状态进行分析，推导不平衡力矩的计算公式，设计有效的自平衡配重方法，分析不平衡自重、风荷载作用、转动速度对转体结构稳定性的影响。

1 工程概况

新建新余市环城路立交桥上跨沪昆铁路，为预应力混凝土T形刚构桥，主跨跨径分布为2m×70m。箱梁截面顶部宽度33.5m，底部宽度23.7m～26.3m。梁高最厚处7m，最薄为3m，梁底成二次抛物线变化。

转动体系由墩柱、转动系统和牵引系统构成。采用平面直径750cm上球铰，下转盘球铰平面直径450cm(图1)。转体系统荷载21 000 000kN，转体部分长度132m，桥梁逆时针转动83.58°。

图1 转体系统示意

2 转体系统设计

2.1 转体球铰设计

该工程采用钢球铰，由上下球铰、定位销轴及套筒、型钢骨架组成。转体总重G=21 000t，考虑到称重试验后还需对转动体系进行平衡配重，故球铰承载力还应适当提高，设计中球铰竖向承载力采用G′=30 000t，球铰混凝土计算压应力σ=18.5MPa。计算公式如下：

因计算得到的球铰直径应大于2.9m，又因结构及滑道的空间布置需要，选用D=4.5m。

进一步对填充的四氟乙烯滑动片应力进行检算，共布置φ6cm的聚四氟乙烯片1812块，总面积为51 207.12cm2，平均压应力为：

安全系数为2.44，满足转体要求。

2.2 转动牵引系统设计

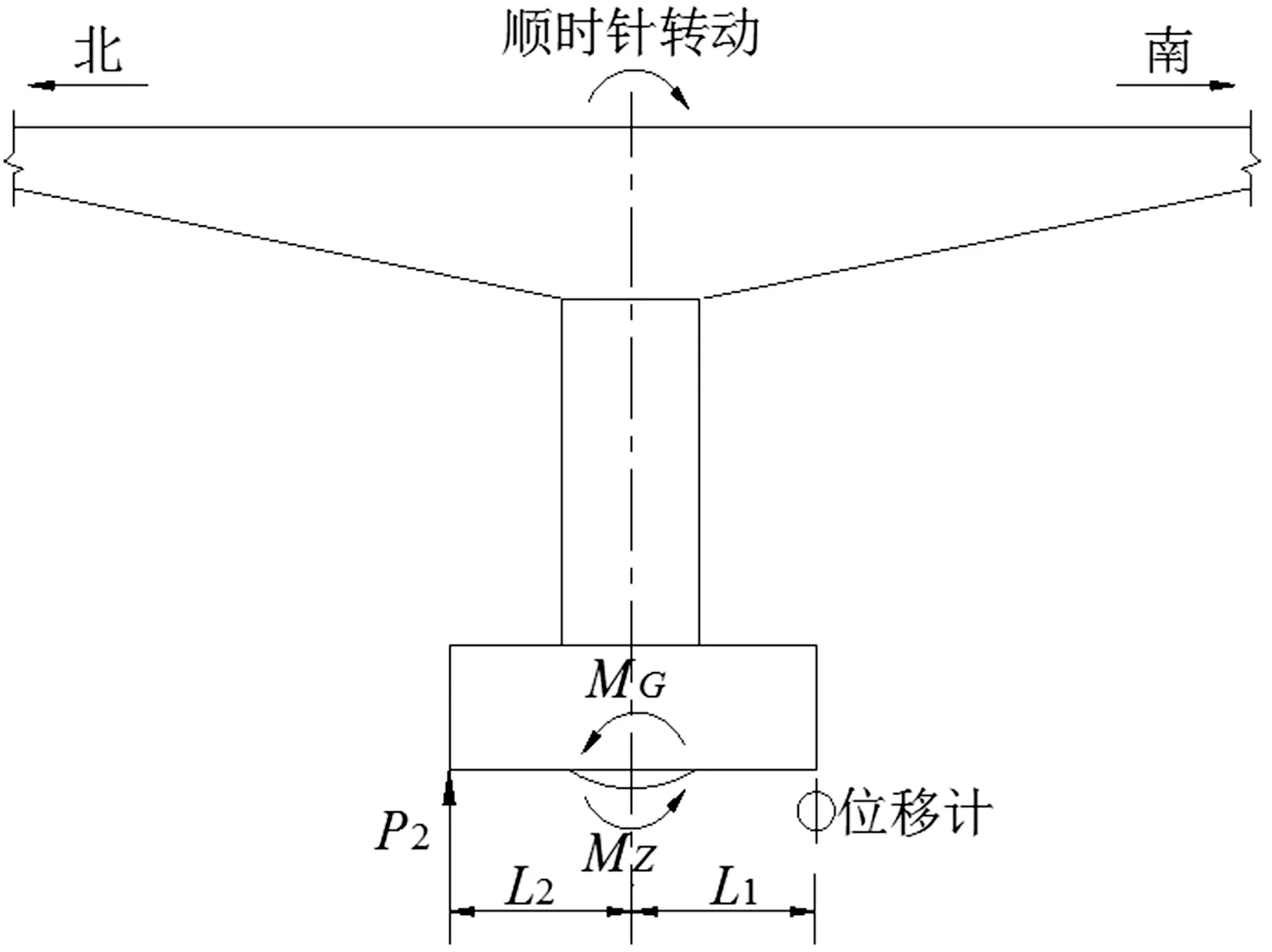
基于通过对转动牵引力计算，可以避免启动惯性失控造成桥梁不安全因素和转体角度产生误差等问题，因此，按照图2对牵引力进行计算。

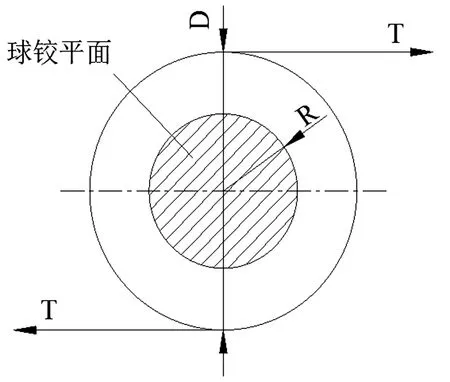
图2 启动牵引力计算平面示意图

假设球铰为平面且应力均匀分布，球铰的转动力矩计算方式如下：

根据《公路桥涵施工技术规范》计算牵引系统的牵引力，即：

式中：

R为球铰半径；

D为牵引力臂；

μ为摩擦系数；

N为荷载。

转体体系由于存在偏心，撑脚和滑道接触，撑脚和滑道之间在转动时存有摩擦力，启动前静摩擦系数取值0.1，启动后动摩擦系数取0.06，T 构的各项参数如下：

启动时所需静摩擦力：

F=21 000×0.1=210t

启动后所需动摩擦力：

F=21 000×0.06=127t

最大启动牵引力：

T1=2Nμ静R/3D=21 000×0.1×2×2.25/3/7.5

=420t；

启动后所需牵引力：

T2=2Nμ动R/3D=21 000×0.06×2×2.25/3/7.5

=252t。

牵引系统设备的选择详见表1。

表1 牵引动力系统组成 台

2.3 平衡保险系统设计

该工程安全系统，包括撑脚、滑道和转盘间保险柱、临时固结；平衡系统，包括结构本身和平衡荷载。

(1)撑脚

在距球铰圆心3.25m圆周上设置6组撑脚。每组撑脚由2根80cm直径、壁厚16mm的钢管组成，其内部填充C50微膨胀混凝土。采用表明光滑的6.3级钢板做为滑道。下转盘混凝土与撑脚同时浇筑完成。

(2)滑道

下球铰外侧顶面安装环形滑道，环带外径r=3.75m，宽0.95m。选用5mm厚钢管作为滑道，调位螺母设置在钢管边缘。滑道下部的角钢支架顶部相对高差不大于5mm，钢板面局部高差不允许大于0.5mm。

3 转体称重试验

3.1 不平衡重称重试验

不平衡重称重试验大多采用球铰竖向转动法。称重时，当顶升荷载较小时，球铰处于静止状态，摩阻力矩等于顶升力矩，球铰处的位移为微小转动变形和上转盘弹性变形之和，顶升力与位移近似线性关系；当顶升荷载较大时，接近球铰最大静摩阻力矩时，整个转动体处在静止和滑动状态之间，摩阻力矩不再增加，如果变成滑动时摩阻力矩还会变小，此时球铰处的位移为转动变形或者球铰发生较大晃动，顶升力与位移不再是线性关系。当主梁脱架完成后，此时梁体的平衡有两种形式：

(1)当球铰摩阻力矩大于不平衡力矩时若桥梁重心偏向北侧，在南侧承台下部逐级加载(图3)，测量顶推力和位移值，记录位移突变值和此处的顶推力P1：

图3 不平衡力矩大于摩阻力矩顶升示意

P1·L1+MG=MZ

(4)

在北侧承台下部使用顶推设备加载(图4)，记录位移值和顶推力，当位移发生突变时，记录下此处顶推力P2：

P2·L2=MG+MZ

(5)

解方程(4)(5)，得不平衡力矩和摩阻力矩：

MG=(P1·L1-P2·L2)/2

(6)

MZ=(P1·L1+P2·L2)/2

(7)

(2)若球铰摩阻力矩小于不平衡力矩时，假设桥梁重心偏向北侧，撤除砂箱后结构北侧的撑脚与滑道接触，因此只能在北侧承台下部逐级加载(图4)，直到使球铰发生微小瞬间转动，记录下其临界顶力P2，得到平衡方程：

图4 不平衡力矩小于摩阻力矩顶升示意

P2·L2=MG=MZ

(8)

当达到顶推力P2后，逐步降低千斤顶顶力(图5)，直到位移计数值发生突变，记录下此处的顶推力，建立平衡方程：

P2·L2=MG-MZ

(9)

解方程(8)(9)，得到不平衡力矩和摩阻力矩：

MG=(P2·L2+P2·L2)/2

(10)

MZ=(P2·L2-P2·L2)/2

(11)

3.2 球铰静摩擦系数和转动体偏心矩计算

球铰处的摩擦力直接影响牵引力的大小，需要对摩擦力矩进行精确计算。其受力简图如图6所示，工程推导如下：

图6 不平衡重状态下主梁竖向位移

静摩阻力矩微元：

静摩擦力微元：

dF=μ0·σs·dA

球铰表面任意一点处面积微元 ：

dA=Rssinθ·dφ·Rs·dθ

作用于球铰下表面的压应力：

σs=σ·cosθ

转体T构对球铰上表面的名义压应力：

对于该桥球铰平面至球心连线与竖直方向Oz轴间的夹角为：

α=arcsin(Rp/Rs)=7°32′51″

由式(12)可得球铰静摩阻系数和转动体偏心距：

3.3 称重设备及测点布置

称重试验选择千斤顶放置上下转盘之间进行，根据估算结果，在主桥转动体墩顶的北侧和南侧各布置2台400t千斤顶，距离球铰中心距离(纵桥向力臂)均为6.0m，千斤顶和测点布置示意图如图5所示。

图5 测点布置示意

在称重时对转体结构进行顶推，获取实时的顶推数值，转盘两侧的力差即为不平衡重量。同时，在球铰四周及南北端中部共布置6个位移计，实时测试转动体在称重过程中是否发生转动，测出球铰由静摩擦状态到动摩擦状态的临界值。

4 主要影响因素分析

4.1 自重不平衡影响分析

现浇主梁两侧的自重不平衡在转体启动时将产生一个不平衡力矩，使其稳定性受到影响，主梁的转体形态及转向速度也将难以控制。假设右侧主梁自重增大为原来的1.03倍、1.05倍、1.07倍、1.1倍，左侧主梁自重不变。对应的主梁竖向位移如图6所示。

由图6可以看出，随着右侧自重的增大，刚体向右倾斜，位移也同时增大。与此同时左侧位移随之减小；挠度与自重不平衡程度成正比，两者呈线性关系。根据规范规定[16]，主梁悬臂端挠度应控制在L/600，该工程中主梁远端最大挠度不应大于116.7mm。当重量比值超过1.05倍后，主梁挠度均大于容许值。由分析可知，该工程应将悬臂重量比值控制在1.05倍范围内。

4.2 风荷载作用影响分析

为考虑多种风荷载对转体结构的影响，分析时，按不低于5年的重现期风速取值，并根据《公路桥梁抗风设计规范》[17]中静力阵风风速进行风荷载计算，4种工况分析情况如表2所示。

表2 4种工况的主梁风荷载组合

图7为不同工况风荷载时主梁横向变形曲线。主梁位移达到7mm在工况4时。梁体横向变形逐渐减小随着工况3到1。

图7 静风荷载作用下主梁横向位移

4.3 转体角速度影响分析

匀速转体阶段在整个转体过程中占时最长，在转动过程中主梁产生的离心力与转动角速度的平方成正比，即F=mω2r。转速过快会对转体稳定性造成严重影响，并在主梁根部截面处产生拉应力。所以，转体施工要在小转速下进行，被较多选用的转体角速度为0.02rad/min。以其为基准，设计了5中转速，主梁的拉应力在不同转速下的应力情况如图8所示。

图8 不同转速下主梁拉应力

由图8可见，当转速小于0.1rad/min时，主梁应力值小于0.1MPa，偏安全。随着主梁转速增加，主梁各控制节点上的应力也在增大，增幅与主梁转速呈二次关系。因此，在实际工程中应将转速控制在较小的范围内，以防主梁混凝土开裂。

5 结论

本文以新余市环城路立交桥上跨沪昆铁路转体桥(2m×70m T形刚构)为工程背景，通过力矩平衡关系式计算摩阻力矩和不平衡力矩，确定自平衡转体施工所需配重大小和配重位置，并通过纵向倾斜配重方法对桥梁转体自平衡体系实施配重设计，该方法具有较高的精确性与适用性。同时，结合工程实例对桥梁转体施工过程中的主要影响参数进行分析，结果表明两侧主梁自重差值应尽量不大于5%，且转动速度控制在0.1rad/min范围内较为安全。