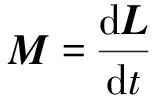变转动惯量的刚体转动问题分析*

邢 杰 张自力 赵长春 郝会颖

[中国地质大学(北京)数理学院 北京 100083]

1 变转动惯量问题的提出

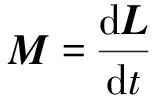
唐军杰等人之前研究过变转动惯量刚体定轴转动的实验研究和数值模拟，在他们的实验中，转动惯量的变化都是因为附加机构质量或质量的分布发生改变引起的[1,2].其实，在最简单的两刚体系统中，转动惯量就已经在变化了，如例1所示.

【例1】一定滑轮固定于O点，定滑轮可以看成是一个质量均匀分布的圆盘，圆盘半径为R，质量为m1.绳子一端固定并绕在轮轴上，另一端挂一质量为m2的物体，自然下垂.绳子的长度不变，质量不计，绳与滑轮之间无相对滑动，求滑轮转动的角加速度.

在这个问题中，一般参考书的解法有两种，第一种：隔离法，第二种：整体法.我们先给出这两种方法.

隔离法：将滑轮m1和物体m2分别做受力分析，然后列动力学方程.对m1来说，滑轮做定轴转动，利用转动定律M=Jm1α，得到

TR=Jm1α

(1)

对于m2，可以看成质点，在本身重力和向上的拉力作用下做竖直向下的直线运动.利用牛顿定律，有

m2g-T′=m2a(T=T′)

(2)

再根据运动学关系

a=Rα

(3)

式(1)～(3)联立，可以求出角加速度

整体法：将m1和m2看成一个整体，这个系统所受的合外力矩是m2gR，它们在外力矩的作用下做定轴转动，根据M=J总α，这里转动惯量

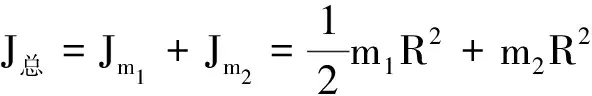
(4)

代入后，可得

这个结果和隔离法的结果一致.

2 等效转动惯量的证明与结论

整体法的处理方法在一些刚体的轮轴问题中经常能看到[1～4]，但是仔细考察后发现式(4)中m2的转动惯量并不好理解.在整个运动过程中，m2相对于转轴的位置总在变化，为什么可以等效成m2R2这一常量表达呢？为了解释清楚这个问题，我们画了图2.

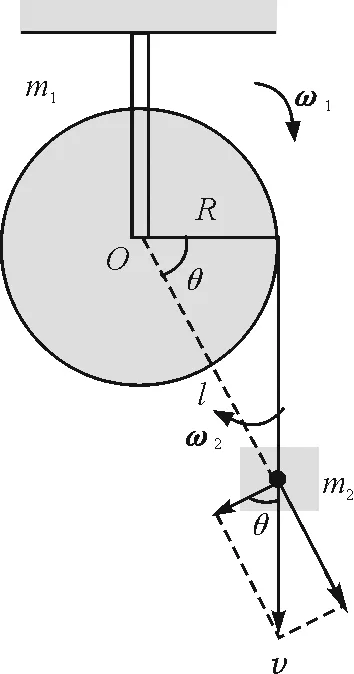
图2 转动惯量分析

这个复合体系中有两个刚体，其中一个刚体m2相对于转轴的位置不断随时间变化，因此我们把总角动量L写成两部分，即

L=Jm1ω1+Jm2ω2

(5)

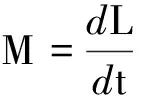
其中圆盘m1的转动惯量Jm1是一个常数，其余参量(ω1，Jm2，ω2)都是时间的函数，于是有

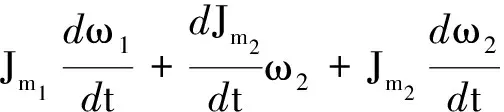
(6)

根据图2和运动学关系，可以得到m2的转动惯量Jm2和角速度ω2

(7)

(8)

这里v表示m2的运动速度，将式(7)和式(8)代入式(6)中，有

(9)

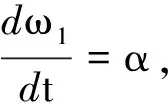
(10)

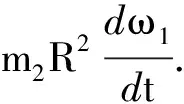
以上是从物理学角度导出了例1这一典型运动模型的运动特点和规律，式(10)与定轴转动刚体的转动定律M=Jα比较可得以下结论：

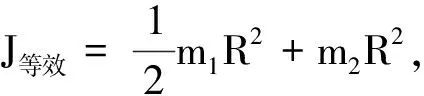
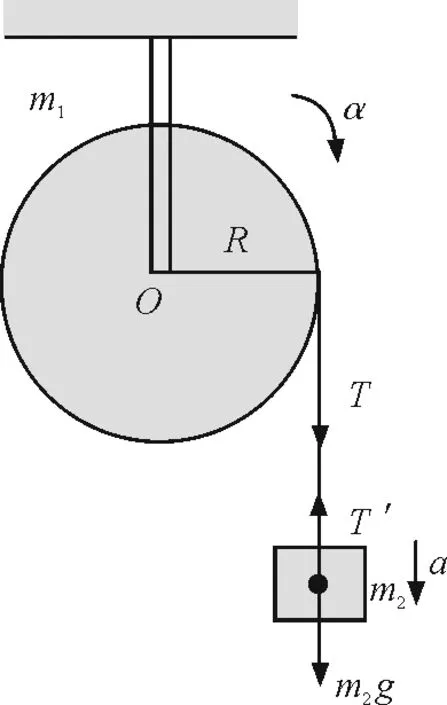
图1 滑轮定轴转动

在普通物理学课程中，一般不定义也不讲解“等效转动惯量”的概念，而在机械原理和机电一体化专业课程中，严格定义讲解了“等效转动惯量”的概念并用于机电工程设计中[5].其中“等效转动惯量”定义的实质和规则是：一个由若干个移动(平动)部件和转动部件构成的系统，其各部件动能之和等于一个等效的定轴转动刚体的转动动能，这个刚体的转动惯量即为等效转动惯量.

按照以上定义和规则，可求出图1所示重物滑轮系统的等效转动惯量，过程为

即有

这就从不同学科的角度证明了“等效转动惯量”概念的正确性和合理性.

3 结束语

有些教材和文献直接用公式M=(Jm1+m2R2)α来进行动力学计算，而且未对式中m2R2做任何注释[1,2,4]，这样很容易让学生误读，学生以为Jm1+m2R2就是刚体系定轴转动的实际总转动惯量，而且总转动惯量是不变的.甚至一些教师也这样认为.笔者翻看了近几年的大学物理教材，一些教材在处理这类轮轴问题时，仍然采用隔离法求解，很少用等效的方法[6～8]，可能也是怕引起误解.