基于真实问题指向素养培育的教学设计——以“生活中的圆周运动”为例

齐国元

(浙江省杭州第四中学 浙江 杭州 310018)

1 教学内容与学生分析

从知识结构上看，学生已经具有受力分析、牛顿运动定律以及圆周运动的相关知识，具备从动力学研究生活中圆周运动的知识储备.“生活中的圆周运动”是学生所学圆周运动知识在现实生活中的具体应用，课堂教学应该让学生充分经历实际问题解决的基本程序：问题呈现—提出方案—推理论证，促进学生思维的发展和素养的形成[1].

从认知结构上看，高一的学生具有大量生活中圆周运动的感性认识，但缺少理性分析生活中圆周运动的经历.本课题的教学核心目标是让学生从物理视角看生活中的圆周运动，利用所学的知识解决实际问题，让学生从物理学角度理性认识生活中的圆周运动，实现对世界的观察从感性认识到理性认知的升华[2].

2 任务分解

任务1：圆周运动力学条件的研究.

任务2：基于真实数据推理论证赛道中的汽车在转弯时是否会发生危险(离心运动的条件).

任务3：为了防止赛道中的汽车做离心运动提出具体的方案并论证其可行性.

任务4：生活中竖直平面内圆周运动问题处理.

3 教学活动

任务1：圆周运动力学条件的研究.

复习问题：该环节旨在让学生理解向心力在圆周运动中的作用，建立圆周运动力学条件的物理观念.问题如表1所示.

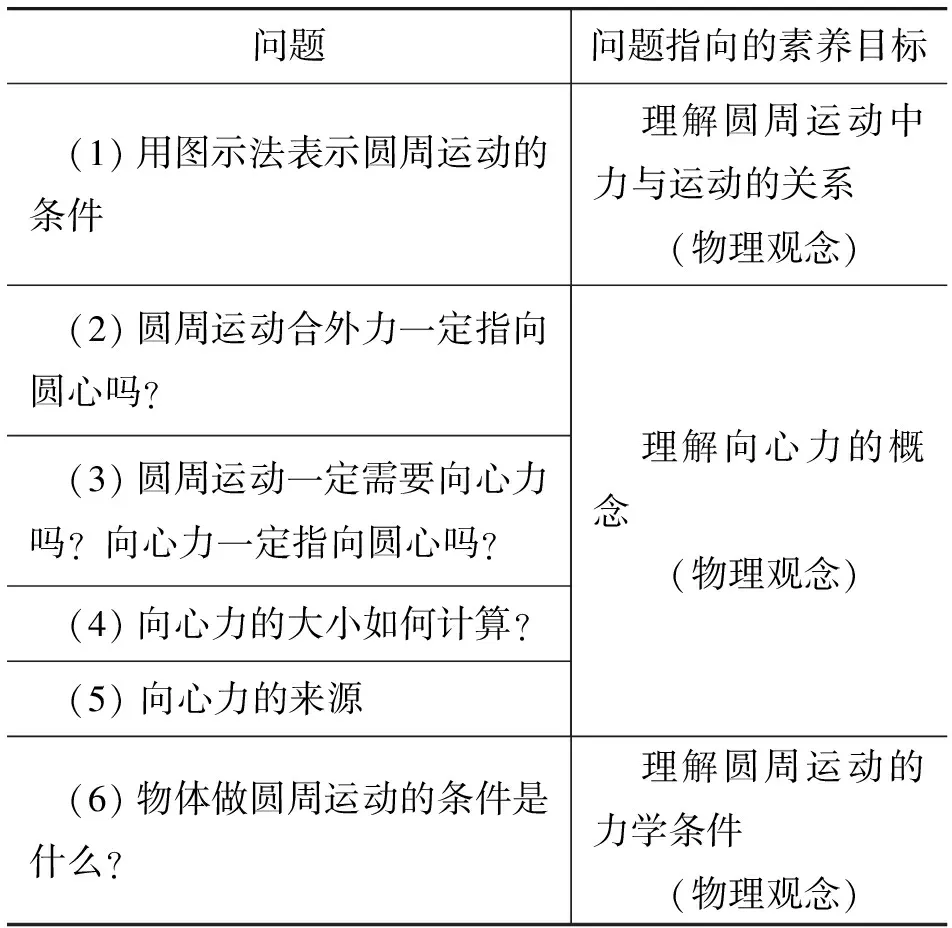
表1 圆周运动力学条件研究中的问题与素养目标

教学建议：

(1)思维引导建议.“圆周运动合外力不一定指向圆心”是学生思维上的一个难点[3]，建议教师在教学过程中通过力与速度的示意图来分析匀速圆周运动和变速圆周运动中，力与速度的关系.

(2)教学活动建议.该任务中的问题学生基本能解决，建议教学中让学生评价学生的回答，以加深学生对圆周运动力学条件的理解.

任务2：基于真实数据推理论证赛道中的汽车在转弯时是否会发生危险(离心运动的条件).

问题情境：该环节旨在培养学生处理实际问题的能力，通过模型建构、科学推理、科学论证、质疑创新来实现科学思维的培育.

如图1所示为一水平赛车跑道的俯视图(不计路面的宽度)，赛道由两条直道(AB,CD)和一个半圆赛道(BC)构成.一赛车(可视为质点)沿赛道从A处经B,C到达D处.

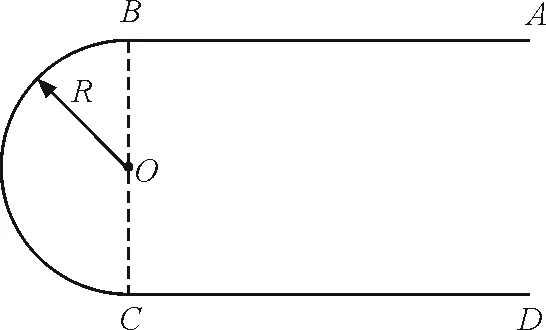
图1 赛车跑道俯视图

要求：在最短的时间走完赛道，如果你是赛车手你会怎么操控赛车？(问题如表2)

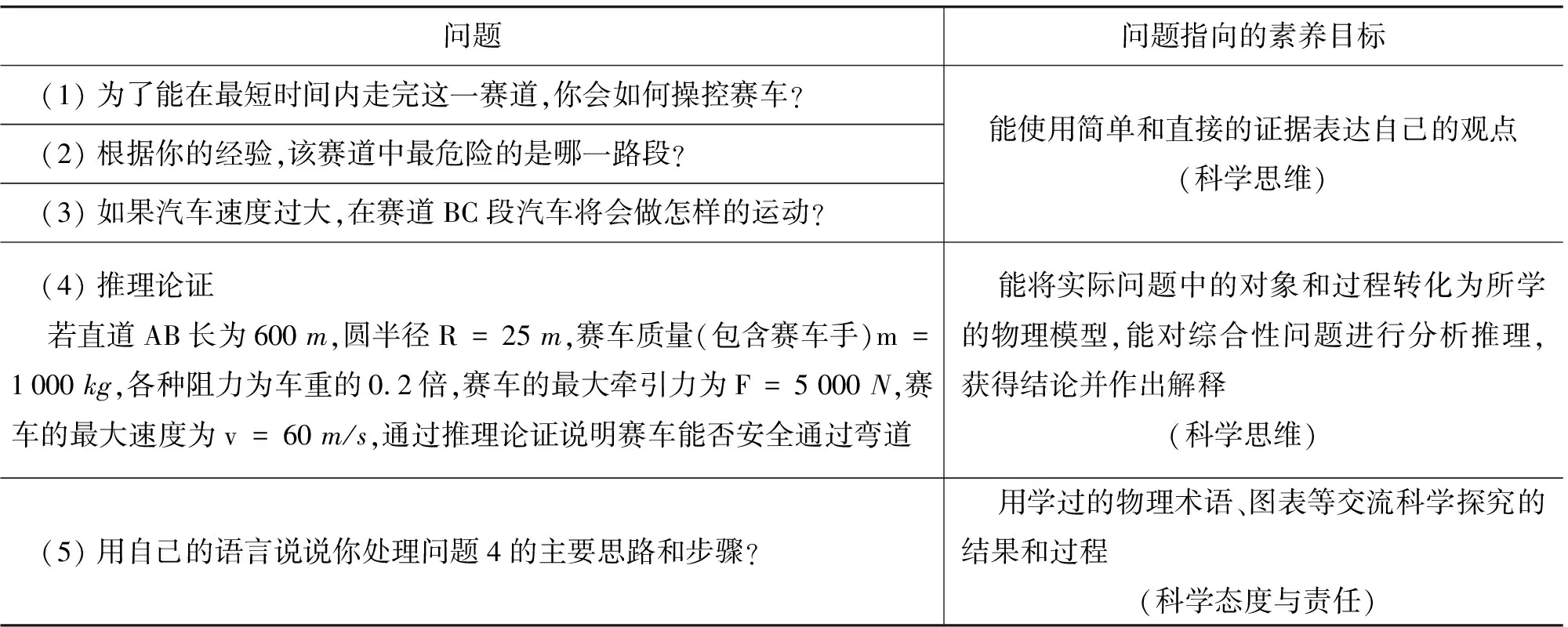
表2 操控赛车运动的问题与素养目标

教学建议：

(1)思维引导建议.学生对离心运动有感性的认识，但缺乏物理视角下理性的认知，建议教学中培养学生用数据来表达自己的想法和结论.通过问题的解决提炼出解决实际问题的一般模式：真实情景—模型建构—推理论证—得出结论.

(2)教学活动建议.该教学环节是本课题教学的重点，建议教师要给予学生充足的时间来自己完成，把学生在处理实际问题中的困难充分地暴露出来.

任务3：为了防止赛道中的汽车做离心运动提出具体的方案并论证其可行性.

问题呈现：该环节旨在让学生直面真实问题，基于所学的物理知识提出可行性方案，并加以论证说明，提升学生的质疑创新能力，问题如表3所示.

表3 防止赛道中的汽车做离心运动分析中的问题与素养目标

教学建议：

(1)思维引导建议.这是一个培育学生科学思维的好案例，建议教师按照：模型构建—科学推理—科学论证—质疑创新的思维路线开展教学.

(2)教学活动建议.学生根据生活经验对这个问题有话可说，建议教师对于问题(1)和问题(2)在教学中让学生大胆地提出自己的方案，并让学生对学生提出的方案进行评价.问题(3)和问题(4)要让学生把实际问题转化为物理模型，经历实际问题处理的过程.

任务4：生活中竖直平面内圆周运动问题处理.

问题情境：本环节旨在培养学生把实际问题转化为所学物理模型的能力，突出模型建构的过程.

如图2为一拱形桥，一汽车正驶过拱形桥，若汽车要安全通过桥面，则在最高点汽车运行速度是大一点好还是小一点好？问题如表4所示.

表4 汽车安全驶过拱形桥分析中的问题与素养目标

图2 汽车驶过拱形桥

教学建议：

(1)思维引导建议.引导学生把实际生活中的生活语言转化成物理术语，这是解决实际问题的一个重要环节.建议教师做好一般曲线运动到圆周运动模型建立的铺垫，通过桥的半径不断变大直到地球半径,培养学生知识的迁移能力，为后续万有引力的学习做好铺垫.

(2)教学活动建议.竖直平面内圆周运动是生活中非常常见的物理模型，若教学时间允许可以增加“汽车过凹桥”“水流星”等模型,让学生自主分析，以培养其对实际问题的分析解决能力.