基于升沉补偿的钻柱-采油树纵向下放安装研究
2020-09-29方海辉王安义
王 川,方海辉,那 枫,金 浩,王安义,刘 静
(1.西南石油大学机电工程学院,四川成都610500;2.中国石油技术开发有限公司,北京100009;3.中国船舶重工集团公司第七一四研究所,北京100101;4.国家油气钻井装备工程技术研究中心,陕西宝鸡721002)
采油树系统下放安装过程比较复杂,容易受到波浪和海流等各种恶劣环境因素的影响。在下放过程中需要控制采油树的下放精度,否则会影响采油树下放的安全以及采油树与井口的对准安装。目前许多学者对采油树的安装稳定性展开了相关研究,如:Bai等[1]介绍了利用隔水管安装采油树的方法,并进行了安装安全性分析;Hu等[2]研究了采油树下放和与井口对接的2个阶段,分析了海洋环境中立管的应力和位移;Zhang等[3]给出了在安装过程中应对绕线和其他操作风险的解决方案;林秀娟等[4]根据在海洋环境中的实际安装工况,建立了深水采油树在下放过程中钻柱的横向力学分析模型,讨论了一些基本参数对钻柱的应力、位移的影响;龚铭煊等[5]根据安装工况建立了在采油树下放安装过程中钻杆的力学分析模型,但未考虑升沉补偿装置以及钻柱的纵向振动;肖易萍等[6]介绍了水下采油树的发展、构造以及不同类型采油树的优缺点,研究了采油树下放安装的步骤与要求;叶永彪等[7]介绍了水下卧式采油树的结构及采油树的主流类型,并总结了水下采油树采用动态定位船吊机下放安装的几个要点。脱浩虎等[8]用OrcaFlex软件建立了水深为1 500 m时采油树下放安装过程的数值仿真模型,研究环境差异等因素对采油树横向偏移和受力的影响。
目前,针对采油树安装稳定性的研究,主要是分析钻柱横向振动的影响,并没有考虑采油树的纵向振动以及其与海底井口连接时开启升沉补偿装置导致的振动的影响。本文针对钻柱-采油树安装模式,建立钻柱-采油树纵向振动动力学仿真模型,考虑平台的升沉补偿,定量研究升沉补偿模式、PID控制器比例函数、补偿缸体积、水深、钻柱壁厚、采油树质量等因素对钻柱-采油树纵向振动性能的影响,以对采油树现场下放安装提供一定的参考。
1 水下采油树安装工况分析
水下采油树在刚开始下放时,与平台的连接为刚性连接。通过钻柱一直下放到井口,到井口附近开启与钻柱上端连接的升沉补偿装置,以确保水下采油树与海底井口安装对接的稳定性。采油树从下放到安装结束一直处于悬挂状态,如图1所示[9]。图1(a)中钻柱与平台为刚性连接,称为采油树硬悬挂;图1(b)中钻柱与平台通过升沉补偿装置连接,称为采油树软悬挂。

图1 采油树悬挂模式示意图Fig.1 Schematic diagram of production tree suspension mode
为了更好地分析和计算,作如下假设[10-14]:
1)钻柱为均质、各向同性的等截面圆管;
2)钻柱上端与平台上的升沉补偿装置相连,钻柱下端与采油树相连,将采油树视为集中质量块悬挂在钻柱的底部;
3)忽略钻柱内部流体对钻柱的影响。
2 基于升沉补偿的钻柱-采油树纵向振动动力学模型的建立
2.1 钻柱-采油树纵向振动动力学分析
钻柱-采油树结构如图2所示,其中L为钻柱的长度。将钻柱底部的采油树视为坐标原点,沿水深方向为x向,水平方向为y向,建立钻柱-采油树纵向振动动力学模型。钻柱微元段力学模型如图3所示,其中:E为钻柱弹性模量,Pa;A为钻柱截面积,mm2;mz为钻柱微元段质量,kg;u(x,t)为距离坐标原点为x的钻柱微元段的纵向振动位移,m;v为海水的线性阻尼系数;g为重力加速度。
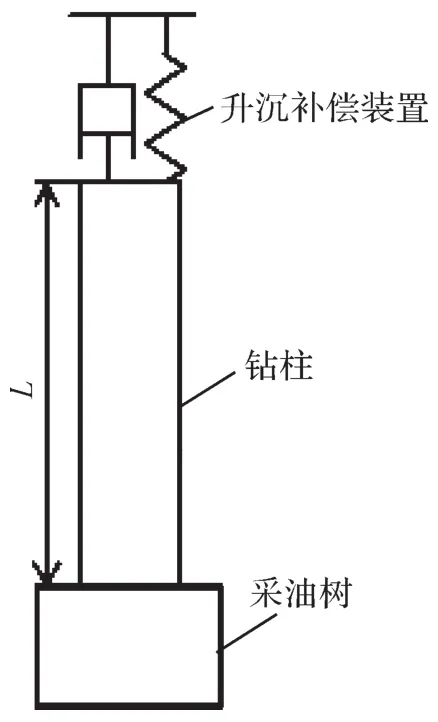
图2 钻柱-采油树结构示意图Fig.2 Structural diagram of drill string-production tree

图3 钻柱微元段力学模型Fig.3 Mechanical model of micro-segment of drill string
距离坐标原点为x的钻柱微元段受到的纵向应力F(x)可以表示为:

在x+dx处钻柱纵向应力可以表示为:

根据牛顿第二定律,钻柱纵向振动微分方程为:

整理式(3)可得:

式中:mg=mz/dx。
2.2 升沉补偿装置力学分析
升沉补偿装置近似于一个大型的气液弹簧,由波浪引起的钻柱升沉运动在补偿装置的作用下会减小振幅,在实际应用中可通过调节补偿缸的压力来适应不同井深的钻柱。主动式升沉补偿装置的工作原理如图4所示。

图4 主动式升沉补偿装置工作原理示意图Fig.4 Schematic diagram of working principle of active heave compensation device
设定:将升沉补偿装置补偿缸内的气体视为无重力的弹簧,其黏性阻尼系数为c1,等效刚度为k1,N/m;升沉补偿装置与钻柱连接的钢丝绳等效为弹簧,其等效刚度为k2,N/m。
当平台上升时补偿缸活塞的受力如图5所示,其中:x1为平台上升位移,m;F1为弹簧恢复力,平台上升时补偿缸内气体被压缩,则F1方向向上,F1=k1(x1-x2),N;f1为补偿缸液阻尼力,方向向上,N;F2为钻柱对活塞的作用力,方向向下,N;Fa1为活塞、活塞杆的惯性力,与活塞运动方向相反,方向向下,N。

图5 平台上升时补偿缸活塞受力示意图Fig.5 Diagram of compensation cylinder piston force with the platform riseing
通过受力分析,得到活塞和钻柱的动力学方程为:

式中:x2为补偿缸活塞的位移,m;m2为活塞和活塞杆的质量,kg。
设x3为升沉补偿装置与钻柱之间的弹性伸长量,其值为平台上升位移与活塞杆运动位移的差值,通过分析可知:

分别对式(5)至式(7)进行拉普拉斯变换,可得:

整理式(8),得活塞位移和平台上升位移之比的拉氏变换为:

同理,当平台下沉时对补偿缸活塞进行力学分析,得到的拉氏变换公式和式(9)相同。
2.2.1 补偿缸等效刚度k1的求取
由理想气体状态方程和弹簧等效刚度的定义可得:

式中:V0为初始工作时补偿缸内气体的体积,V1为活塞杆运动后补偿缸内气体的体积,m3;p0为补偿缸内气体的初始压力,p1为补偿缸内气体的体积为V1时气体的压力,MPa;n为多变指数,等温过程中n=1.0,绝热过程中n=1.4,本文取n=1.0;A2为补偿缸有杆腔工作面积,m2。
由式(10)可解得:

2.2.2 钢丝绳等效刚度k2的求取
根据前文的设定,由材料力学可得钢丝绳等效刚度k2为:

式中:E1为钢丝绳弹性模量,Pa;S1为钢丝绳的截面积,m2;l为钢丝绳的长度,m。
2.3 钻柱-采油树纵向振动动力学模型的边界条件
平台随海浪升沉的运动经升沉补偿装置作用后施加在钻柱的顶部。将升沉补偿装置作用后平台的位移看作钻柱-采油树纵向振动动力学模型的上边界条件。
钻柱底部连接采油树,将采油树看作钻柱底部的附加集中质量块,则钻柱-采油树纵向振动动力学模型的底部边界条件可以表示为:
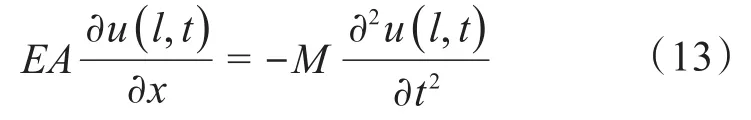
式中:M为采油树质量,t。
3 基于有限差分法的钻柱-采油树纵向振动动力学模型求解
3.1 有限差分法的基本思路
钻柱-采油树纵向振动动力学模型包含对时间和空间的二阶偏导方程,采用有限差分法对钻柱-采油树纵向振动动力学模型求解[15-19]。其基本思路为:
1)利用差分网格对偏微分方程的求解域进行划分;
2)利用向前差分法离散微分方程组,得到方程组的差分格式;
3)将定解条件进行离散,导出相应的离散化差分格式;
4)通过迭代法得到偏微分方程定解区域内的解。
3.2 方程组差分的格式
将钻柱视为一个梁单元,沿x方向均匀划分m段,共有m+1个节点,每段长度为h。自下而上依次给节点i编号,i=1,2,…,m,m+1。模型计算时间为t,用Δt表示时间间隔,对时间进行离散,得到j个时间节点,j=1,2,…,b,b+1,则钻柱的i节点在j时刻的位移为ui,j。
根据有限差分法可得到差分公式,把差分公式代入式(4)和式(13),可以得到钻柱-采油树纵向振动微分方程的差分格式为:


3.3 模型求解
在上一节已经求解出升沉补偿装置活塞位移与平台升沉位移之比的拉氏变换,在MATLAB中搭建升沉补偿装置的Simulink模型,如图6和图7所示。主动式升沉补偿装置可以通过检测活塞的位移信号,获得钻柱移动的位移,并主动进行补偿以保持钻柱位置的平衡。本文采用PID(proportion integration diferentiation,比例积分微分)控制器作为主动式升沉补偿装置的控制模块,该控制器具有算法简单、稳定性和可靠性好等优点。

图6 主动式升沉补偿装置的Simulink模型Fig.6 Simulink model of active heave compensation device

图7 被动式升沉补偿装置的Simulink模型Fig.7 Simulink model of passive heave compensation device
将模型运行后的仿真数据保存到MATLAB的工作区间,作为钻柱-采油树纵向振动动力学模型的上边界条件。式(14)所示的差分方程组有m+1个未知量,通过MATLAB编程对该封闭方程组(m个方程组及上边界条件)求解。
4 实例仿真与结果分析
某井位作业环境水深为1 500 m,海水密度为1 030 kg/m3,钻井液密度为1 600 kg/m3;钻柱外径为127 mm,钻柱壁厚为10.92 mm,钻柱密度为7 850 kg/m3,钻柱的弹性模量为206 GPa;采油树质量为40 t,平台升沉运动振幅为2 m,运动周期为30 s,补偿缸体积为1 m3,PID控制器的参数为:kp=8,ki=2.0,kd=1.0。
基于以上基本参数,讨论升沉补偿模式、PID控制器比例系数、补偿缸体积、水深、钻柱壁厚和采油树质量等因素对钻柱-采油树纵向振动性能的影响。
4.1 升沉补偿模式的影响
保持其他参数不变,分别采取硬悬挂被动式升沉补偿模式(以下简称为被动模式)、主动式升沉补偿模式(以下简称为主动模式)进行仿真分析。图8所示为不同补偿模式对钻柱-采油树纵向振动性能的影响。
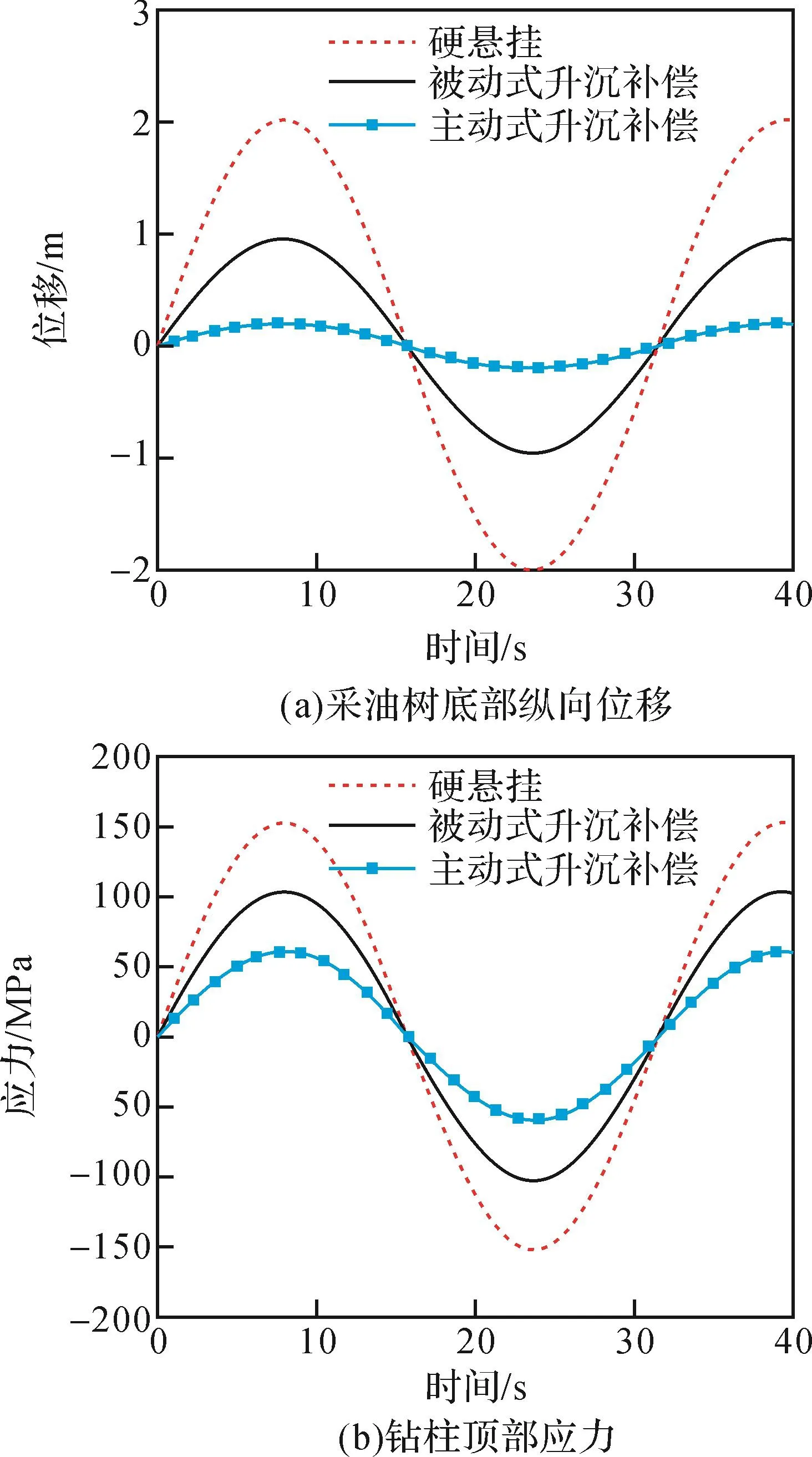
图8 不同补偿模式对钻柱-采油树纵向振动性能的影响Fig.8 Influence of different types of compensation modes on the longitudinal vibration performance of drill stringproduction tree
由图8可以看出,采油树底部纵向位移和钻柱顶部应力均随时间呈正弦变化。硬悬挂模式下位移和应力最大,其次是被动模式,最小的为主动模式,说明主动模式效果最优。被动式升沉补偿装置补偿后钻柱-采油树纵向最大位移为0.95 m,补偿率为52.5%;主动式升沉补偿装置补偿后的最大位移为0.18 m,补偿率为91%。因此,在采油树下放时应优先选择主动模式。
4.2 PID控制器比例系数的影响
PID控制器有比例、积分、微分三种调节方式,由于篇幅所限本文仅对PID控制器的比例系数kp对钻柱-采油树纵向振动性能的影响进行分析。在主动模式下,保持其他参数不变,分别取比例系数kp=8,9,10进行仿真分析。图9所示为PID控制器比例系数对钻柱-采油树纵向振动性能的影响。
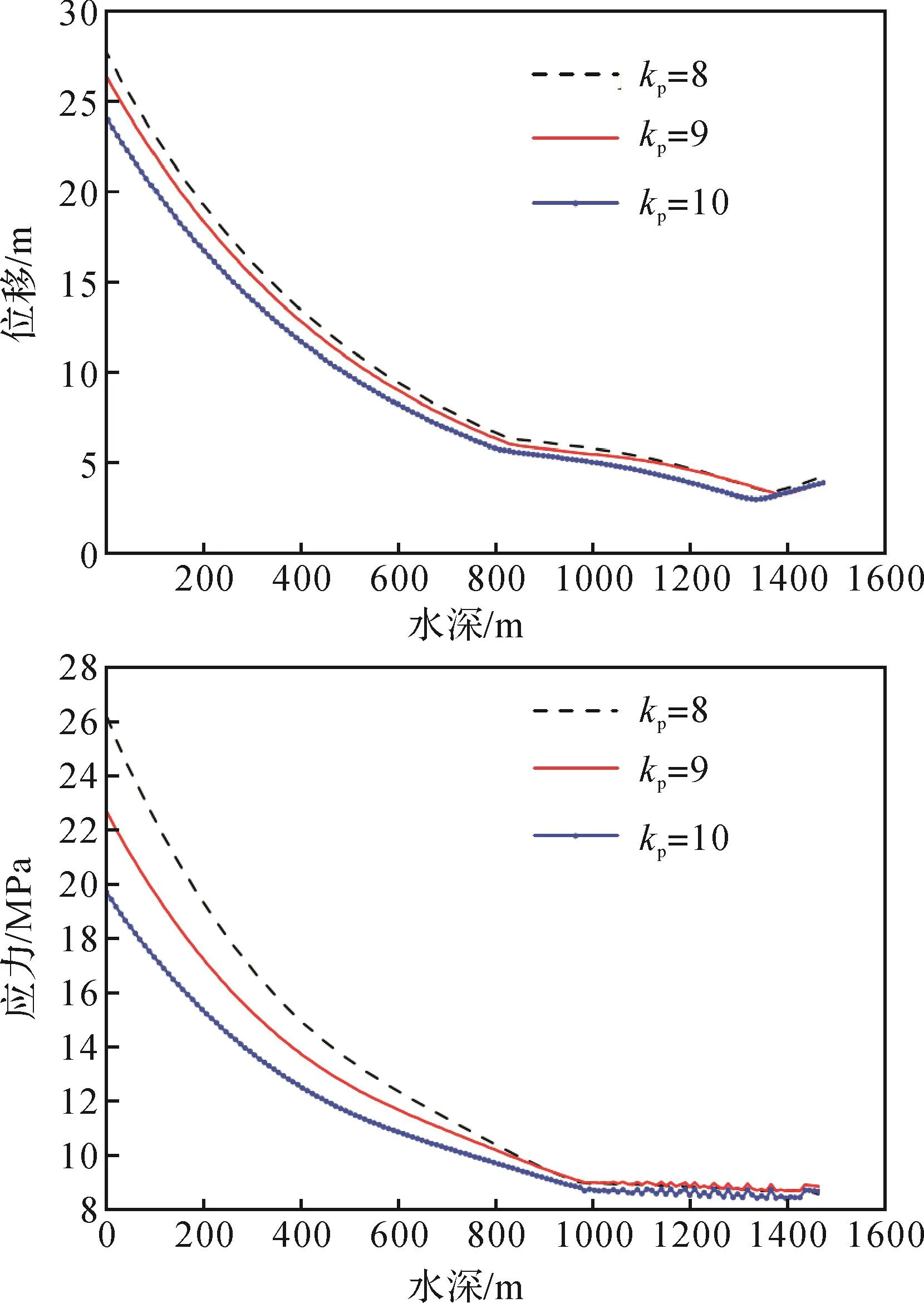
图9 PID控制器比例系数对钻柱-采油树纵向振动性能的影响Fig.9 Influence of PID controller proportional coefficient on the longitudinal vibration performance of drill stringproduction tree
由图9可以看出,随着水深的加大,钻柱-采油树的纵向振动位移及受到的应力逐渐减小,且在1 000 m水深后减小趋势变缓慢。由位移图可以看出,随着kp增大,钻柱-采油树纵向振动位移减小,kp=10时其最大纵向振动位移为23 mm,kp=8时其最大纵向振动位移为27 mm,且在1 000 m水深下钻柱纵向振动位移有重合。由应力图可以看出,随着kp增大,钻柱-采油树受到的应力减小,在1 000 m水深下应力出现波动,说明钻柱-采油树系统不稳定。因此,在主动模式下应该选择合适的kp以确保钻柱-采油树系统的稳定。
4.3 补偿缸体积的影响
保持其他参数不变,分别选取补偿缸体积V=1,10,20 m3进行仿真分析。图10所示为补偿缸体积对钻柱-采油树纵向振动性能的影响,其中,zd表示主动模式,bd表示被动模式。
由位移图可知:在被动模式下,补偿缸体积为1 m3时钻柱-采油树最大纵向振动位移为185.8 mm,补偿缸体积为20 m3时最大纵向振动位移为169.0 mm;在主动模式下,补偿缸体积为1 m3时最大纵向振动位移为37.2 mm,补偿缸体积为20 m3时最大纵向振动位移为33.9 mm;随着补偿缸体积的增大,钻柱-采油树的纵向振动位移减小。

图10 补偿装置气缸体积对钻柱-采油树纵向振动性能的影响Fig.10 Influence of compensation cylinder volume of compensation device on longitudinal vibration performance of drill string-production tree
由应力图可知;钻柱-采油树受到的应力随补偿缸体积的增大而减小;在被动模式下,随着补偿缸体积的变化,钻柱-采油树顶部受到的最大和最小应力分别为122 MPa和111 MPa;在主动模式下,钻柱-采油树顶部受到的最大和最小应力分别为51 MPa和45 MPa。
由上可知,在被动模式下补偿缸体积的变化对钻柱-采油树纵向振动性能的影响较主动模式更明显。
4.4 水深的影响
保持其他参数不变,分别选取水深d=500,1 500,2 500 m进行仿真分析。图11为水深对钻柱-采油树纵向振动性能的影响。
由位移图可以看出:在不同水深条件下,钻柱-采油树顶部纵向振动位移基本相同,沿轴向方向逐渐减小,在钻柱-采油树底部表现出增大的趋势;当钻柱长度增加到1 500 m以后,钻柱-采油树底部纵向振动位移变化很小;在被动模式下,1 500 m的钻柱-采油树底部纵向振动位移为20.1 mm,水深为2 500 m时其底部位移为9.8 mm;在主动模式下,1 500 m的钻柱-采油树底部纵向振动位移为11.8 mm,水深为2 500 m时其底部位移为7.3 mm,而钻柱顶部受到升沉补偿装置的持续激励作用,所以振动位移相同。在主动模式下顶部纵向振动位移为40.1 mm,被动模式下顶部纵向振动位移为114.2 mm,主动模式下顶部振动位移仅为被动模式的35%,可见主动模式的补偿效果优于被动模式。
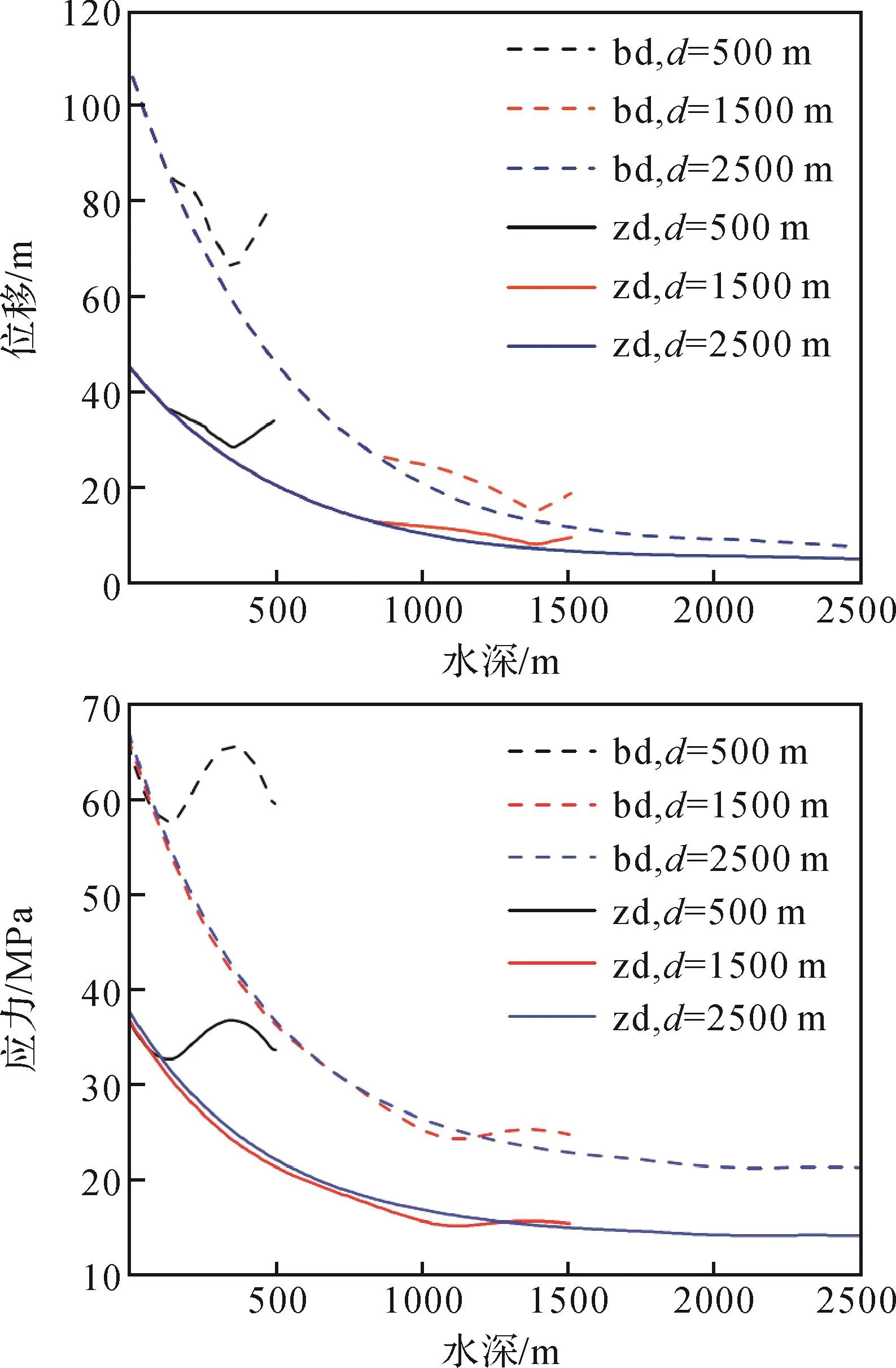
图11 水深对钻柱-采油树纵向振动性能的影响Fig.11 Influence of water depth on longitudinal vibration performance of drill string-production tree
由应力图可以看出;在不同水深条件下,钻柱-采油树顶部受到的应力相差不大;随着水深的增加,应力从顶部到底部表现出先减小后增大的趋势,增大的趋势随着水深的增加而减弱;在被、主动模式下钻柱-采油树受到的最大应力分别为68.1,34.2 MPa,主动模式下钻柱-采油树的应力为被动模式的一半,补偿效果明显。
4.5 钻柱壁厚的影响
保持其他参数不变,分别选取钻柱壁厚D=8.56,10.92,12.7 mm进行仿真分析。图12为钻柱壁厚对钻柱-采油树纵向振动性能的影响。
由图12可以看出:钻柱-采油树纵向振动位移和受到的应力均随钻柱壁厚的增大而减小,且变化趋势在钻柱壁厚较小时更明显;钻柱-采油树顶部响应变化趋势较底部更明显,当壁厚从8.56 mm增大为12.7 mm时,在被动模式下钻柱-采油树最大纵向振动位移减少了92.6 mm,受到的最大应力减少了61.8 MPa;在主动模式下最大纵向振动位移减小了18.5 mm,最大应力减小了28.1 MPa;主、被动模式下钻柱-采油树最大纵向振动位移分别为51.3,256.5 mm,主动模式下最大纵向振动位移仅为被动模式的20.0%,其补偿效果优于被动模式。采油树下放安装时应该选择合适的钻柱壁厚。

图12 钻柱壁厚对钻柱-采油树纵向振动性能的影响Fig.12 Influence of drill string wall thickness on longitudinal vibration performance of drill string-production tree
4.6 采油树质量的影响
保持其他参数不变,分别选择采油树质量M=30,40,50 t进行仿真分析。图13为采油树质量对钻柱-采油树纵向振动性能的影响。
由位移图可知:在深水条件下采油树质量对钻柱-采油树纵向振动位移基本没有影响;在不同采油树质量条件下,钻柱-采油树在0~800 m的浅水区域的振动位移曲线基本重合,而在800~1500 m的深水区域有较小变化;被、主动模式下钻柱-采油树最大纵向振动位移分别为138.3,26.5 mm,主动模式下的最大纵向振动位移仅为被动模式的19.2%。
由应力图可知:钻柱-采油树受到的应力与采油树质量成正比。被动模式下钻柱-采油树顶部受到的最大和最小应力分别为67.88,57.64 MPa;主动模式下钻柱-采油树顶部受到的最大和最小应力分别为29.56,18.58 MPa。
由上可知,采油树质量主要影响钻柱-采油树的应力分布,不影响其纵向振动位移。
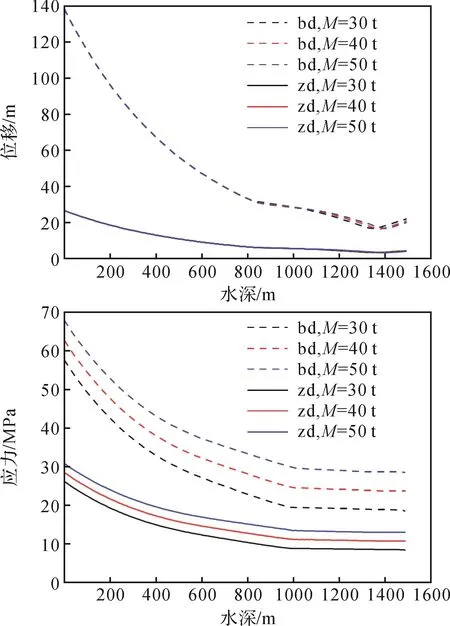
图13 采油树质量对钻柱-采油树纵向振动性能的影响Fig.13 Influence of production tree weight on longitudinal vibration performance of drill string-production tree
5 结论
1)基于动力学基本原理建立了钻柱-采油树在下放安装过程的纵向振动动力学仿真模型,在MATLAB中采用有限差分法对该模型进行离散求解。
2)通过实例仿真可知,在采油树下放安装时,应优先选择主动模式,并且选择合适的PID控制器的系数、补偿缸体积、水深、钻柱壁厚和采油树质量,以提高采油树的安装稳定性。
