基于Helmholtz共振腔阵列的声学超材料研究

张宪旭，刘怡然，李丽君

（山东理工大学交通与车辆工程学院，山东淄博255049）

噪声控制主要有隔声和吸声两种方式。传统隔声材料密度高，厚度大，应用时往往因不满足轻量化要求而受到局限［1-3］；多孔材料等吸声材料在高频段的吸声性能较好，在中低频段的吸声性能较差［4-6］。相比传统隔声材料，声学超材料质量较小；相比传统吸声材料，声学超材料在中低频具有较好的吸声效果。声学超材料带隙产生机理主要有Bragg散射原理和局域共振原理。Bragg散射发生的频率在c/2d（c为介质中的声速，d为晶格常数）附近，所以低频吸声需要较大的晶格尺寸，而局域共振机理主要是靠单个晶格的共振来消耗声能量［7-9］。新型的局域共振型声学超材料给中低频噪声控制提供了新的途径［10-13］。

目前，已有许多学者对声学超材料进行了研究。例如：刘正猷等提出了一种基于局域共振原理的声学超材料：在环氧树脂基体中嵌入由硅橡胶包裹的铅球，并对其吸声性能进行了试验验证，发现在晶格常数为2 mm的情况下，该声学超材料在频率为400 Hz时出现了带隙特征，实现了“小尺寸控制大波长”［14］；杨帆等发现Helmholtz共振腔的腔体体积、几何形状，短管的几何形状、布置位置等都会影响Helmholtz共振腔的共振频率和吸声性能［15］；陈鑫等通过将Helmholtz共振腔和弹性振子耦合，打开了声学超材料的低频带隙［16］；夏百战等基于区间模型对声学超材料进行优化，以波导和周期性Helmholtz共振腔组成的声学超材料为例，分析了不确定参数对声学超材料声强传递系数和负有效体积模量的影响［17］；高东宝等对基于Helmholtz共振腔阵列的二维声学超材料进行了研究，发现Helmholtz共振腔阵列的腔体几何参数和阵列方式均会影响声学超材料的带隙位置［18］；姜久龙等设计了一种双开口Helmholtz周期结构，该结构具有较宽的低频带隙［19］。利用传统声学超材料实现中低频噪声控制需要较大体积或质量。为实现声学超材料结构的小尺寸以及轻量化，笔者基于Helmholtz共振腔的共振特性设计出一种新型的局域共振型声学超材料。

1 基于Helmholtz共振腔阵列的声学超材料的模型设计及吸声性能仿真

1.1 有限元模型的建立

所设计的新型声学超材料由多个Helmholtz共振腔构成，并在晶格结构上作了改进，即优化了单个Helmholtz共振腔的结构。图1（a）所示为单个Helmholtz共振腔模型。取3个尺寸相同的长方体（长为a，宽为b，高为e）模拟共振腔，将圆柱形短管（半径为r，高为h）布置在共振腔的3个非对称面上，即3个Helmholtz共振腔的短管位置各不相同，将3个Helmholtz共振腔阵列，彼此之间留空气间隙波导宽t，得到以3个Helmholtz共振腔阵列为基础的晶格、晶格常数为d的新型声学超材料。本文计算声学超材料模型的空气域，将长a=15 mm，b=13 mm和e=8 mm的长方体作为共振腔，圆柱短管设置为r=1 mm，h=1 mm，Helmholtz共振腔壁厚为1 mm。综合考虑新型声学超材料对声波的透射量和声波能量入射到共振腔的量，设间隙波导宽t=0.5 mm，晶格常数d=3（a+t）=46.5 mm。取单个Helmholtz共振腔进行研究。共振腔基体材料的声阻抗与空气的声阻抗相差较大，所以建立如图1（c）所示单个声学超材料晶格模型，将晶格阵列为图1（d）所示的声学超材料板件模型。

图1 声学超材料晶格与板件模型Fig.1 Models of lattices and plate of acoustic metamaterial

图2所示为基于Helmholtz共振腔阵列的声学超材料计算模型，其x方向周期排列8个晶格。将Helmholtz共振腔壁面设置为硬声场边界；在纵向上设置Floquet periodicity边界条件，以表现y方向的周期性；在左侧添加背景压力声场，单位声压为1 Pa；右侧设置为空气域；为防止硬声场边界的反射声波对传递损失造成影响，在模型最外侧设置完美匹配层。

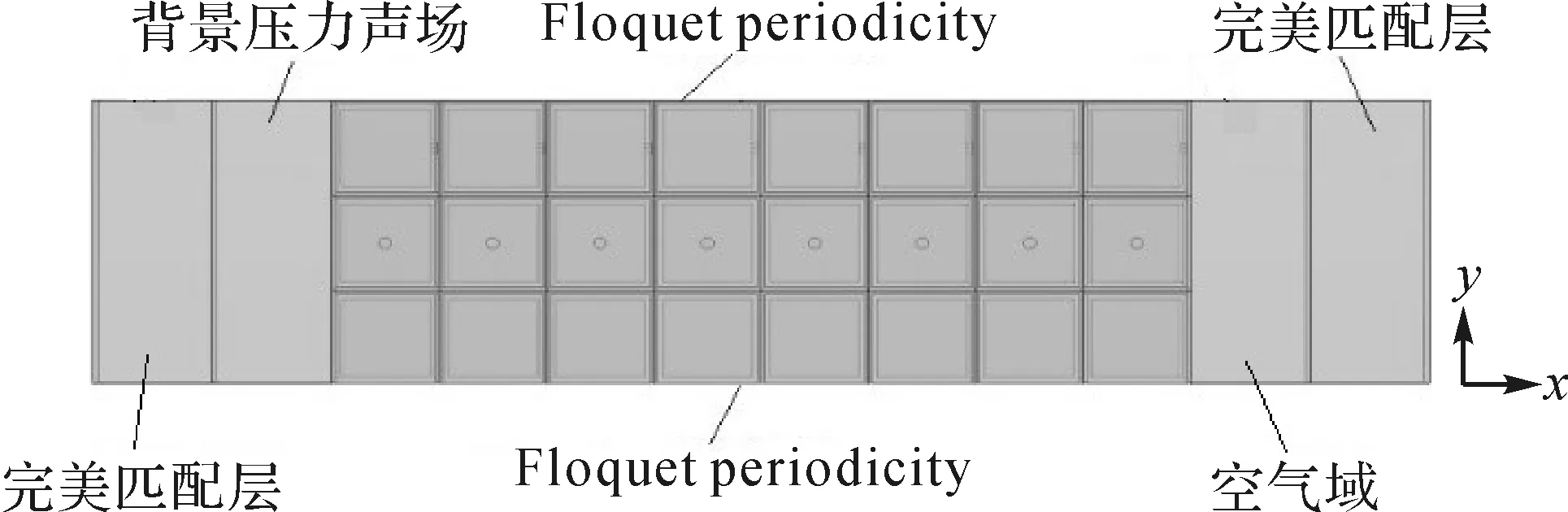
图2 基于Helmholtz共振腔阵列的声学超材料计算模型Fig.2 Calculation model of acoustic metamaterial based on Helmholtz resonant cavity array

1.2 吸声性能仿真

利用COMSOL Multiphysics软件中的声学模块对基于Helmholtz共振腔阵列的声学超材料进行声学性能仿真分析。

对晶格模型依次沿坐标（0，0）、（0，1）、（1，1）、（0，0）进行参数化扫描，得出声学超材料的能带图。分析声波在声学超材料中的传输特性，用传递损失曲线表示。传递损失的计算如下：

式中：TL表示传递损失；win表示入射声能量；wout表示出射声能量。

图3所示为基于Helmholtz共振腔阵列的声学超材料的能带图和传递损失曲线。从图3（a）所示的能带图可以看出，基于Helmholtz共振腔阵列的声学超材料具有3段带隙（1 190～1 226 Hz，1 305～1 353 Hz，1 483～2 509 Hz），这与图3（b）所示的声能损失峰值频域相对应。第1带隙较窄，其频域宽度为36 Hz，最大传递损失达到50 dB；第2带隙也较窄，其频域宽度为48 Hz，最大传递损失接近40 dB；第3带隙较宽，其频域宽度为1 026 Hz，传递损失峰值大，最大传递损失超过80 dB；通带频域对应的传递损失较小，说明在通带频域内声波能量衰减得很少。基于Helmholtz共振腔阵列的声学超材料第1带隙的中心频率约为1 208 Hz，此时波长约为283.9 mm；基于Helmholtz共振腔阵列的声学超材料的晶格常数为46.5 mm，单个Helmholtz共振腔的长度仅为15 mm，而基于Bragg散射机理的周期阵列材料的晶格常数与带隙频率在基体材料中对应波长的一半相当，其对应的晶格常数将达到130 mm。由此可以看出，基于Helmholtz共振腔阵列的声学超材料可以实现“小尺寸控制大波长”。

图3 声学超材料的能带图和传递损失曲线Fig.3 Energy band graph and transfer loss curves of acoustic metamaterial

因组成晶格的3个Helmholtz共振腔的开口方向不同，则该晶格具有3个不同的特征频率。如图3（a）所示，第1带隙、第2带隙和第3带隙的下边缘都出现了平直带，可见在声学超材料内不同方向、不同振动位置，都存在同样的空气振动模式。

作为对比，现将如图1（a）所示具有单一方向开口的Helmholtz共振腔周期阵列，横向阵列8个晶格，纵向阵列3个晶格，传递损失计算模型的排列方式与图2一致，其传递损失曲线如图4所示。

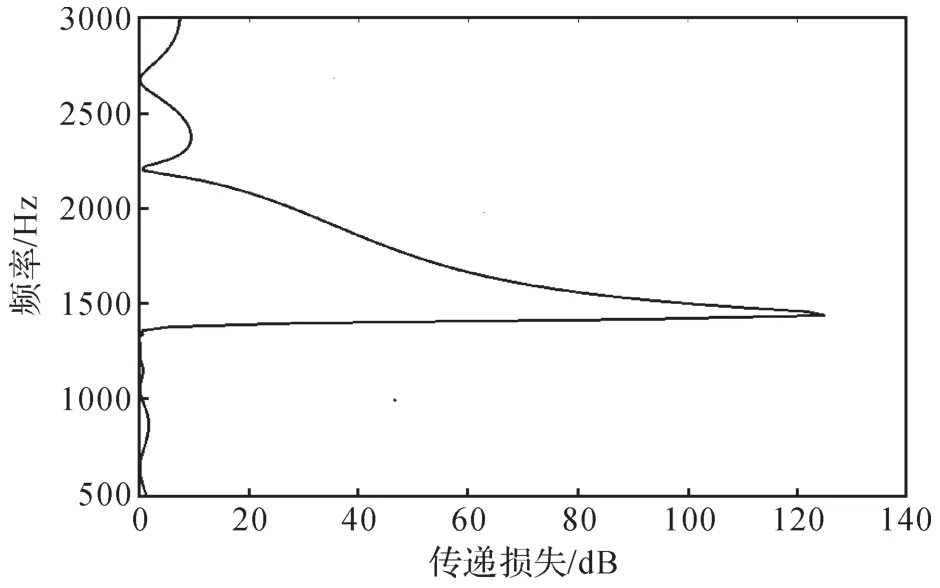
图4 具有单一方向开口的Helmholtz共振腔阵列的传递损失曲线Fig.4 Transfer loss curve of Helmholtz resonant cavity array with a single directional opening

由图3（b）可以看出，具有不同方向开口的Helmholtz共振腔阵列的声学超材料的传递损失曲线在频率小于1 500 Hz时存在2个峰值，在频率大于1 500 Hz时存在1个较大的峰值，这是因为该Helmholtz共振腔阵列具有3个不同的特征频率以及波导也具有相应的特征频率，声波在多个特征频率处因产生共振而被消耗，增大了传递损失的范围；而由图4可知，具有单一方向开口的Helmholtz共振腔阵列的传递损失曲线在频率小于1 500 Hz时并不存在峰值，即传递损失峰值对应的频率范围较小，这是因为具有单一方向开口的Helmholtz共振腔阵列只具有1个特征频率以及波导的特征频率，声波只在2个特征频率处被消耗。

取带隙边界位置频率点的晶格声压分布，以分析带隙边界位置的振动模式，结果如图5所示。

第1带隙下边界频率为1 190 Hz，该带隙下边缘的平直带对应的振动模式为位于声学超材料晶格中间的Helmholtz共振腔腔体发生局域共振，导致共振腔内声压增大，且短管处声压逐渐减小，外部波导处声压最低，如图5（a）所示，此时声波在声学超材料的任意方向入射，晶格的振动模式都为中间的Helmholtz共振腔内空气发生振动，声波能量被局域在共振腔内不能传播。

分析第2带隙内频率点1 332 Hz的声压分布。晶格中上方单个Helmholtz共振腔声压增大，共振腔内的空气产生局域共振，连接共振腔的短管和外部波导声压很低，声波能量不能传播，如图5（b）所示。

综上，第1带隙和第2带隙较窄，频域范围小，在此频域范围内吸声机理是单个Helmholtz共振腔局域共振，声波能量在独立的共振腔内因与空气共振而损耗。

第3带隙下边界为平直带，计算频率为1 483 Hz时的晶格声压，结果如图5（c）所示。此时晶格中下方单个Helmholtz共振腔产生局域共振，腔体内部声压增强，且远大于外波导和其他2个腔体的声压。短管到外部波导的声压变化趋势和第1带隙下边界频率对应的声压变化一致。第3带隙的上边界频率为2 509 Hz，取上边界频率附近频率点2 492 Hz的声压分布，此时局域共振发生在外部的波导处，晶格上方和下方两个Helmholtz共振腔也存在一定的声压，而声压最小的区域出现在短管处，如图5（d）所示。第3带隙是在共振腔共振吸声以及因其周期排列出现的外波导共振吸声联合作用下产生的，所以基于Helmholtz共振腔周期阵列的声学超材料的第3带隙较宽。

图5 晶格上的声压分布Fig.5 Distribution of acoustic pressure on lattice

对如图1（d）所示的基于Helmholtz共振腔阵列的声学超材料板件模型，在其左侧施加单位声压1Pa，计算整体板件的声压分布。将频率为2 000 Hz（带隙频域内）和频率为3 000 Hz（通带频域内）时的声压分布进行对比，如图6所示。

由图6（a）可以看出，声波能量被局域在声学超材料板件前2个晶格内，随着晶格周期阵列数量的增加，声压在周期阵列方向迅速衰减，可以看到右侧第8个晶格的声压水平已经很低。由图6（b）可以看出，声学超材料板件第1个晶格和和后3个晶格的声压较大，中间3个晶格的声压很小，说明频率为3 000 Hz时，声学超材料并无法有效阻止声波能量的传播，在声波入射侧的对侧仍存在较大声波能量。

图6 声学超材料板件上的声压分布Fig.6 Distribution of acoustic pressure on metamaterial plate

2 基于Helmholtz共振腔阵列的声学超材料吸声性能测试

所设计的基于Helmholtz共振腔阵列的声学超材料的晶格尺寸为毫米级，且外部波导宽仅为1 mm。采用3D打印方法制备的声学超材料的共振腔样件如图7（a）所示，基于Helmholtz共振腔阵列的声学超材料样件（350 mm×280 mm）如图7（b）所示。

图7 Helmholtz共振腔样件和声学超材料样件Fig.7 Sample piece of Helmholtz resonant cavity and acoustic metamaterial

为测试所制作的声学超材料的吸声效果，建立一个独立封闭的声场环境（位于560 mm×560 mm×560 mm的木质箱子中）。采用声望OS003A无指向声源：12个扬声器均布在直径为280 mm的球体上，各个扬声器之间采用串-并联的连接方式，以保持其工作相位一致。在此种连接方式下，无指向声源的阻抗与一般功率放大器输出的阻抗相匹配，最终形成一个球面波辐射声源，声源信号为粉红噪声。将声望BSWA MPA416传声器固定在木质箱子内部上方且不与箱壁接触，将声学超材料样件固定在木质箱子内部上方。采用计算机测试软件m+p Smart Office，基于传递函数法对数据采集器采集的数据进行处理，得到有无声学超材料时该声场环境的声压级变化曲线。声学超材料吸声性能的测试设备如图8所示。在上述声场环境中进行多组吸声性能测试，结果如图9所示。

图8 声学超材料吸声性能的测试设备Fig.8 Testing equipment for sound absorption performance of acoustic metamaterial

图9 有无声学超材料时声场环境的声压级变化曲线Fig.9 Variation curve of acoustic pressure level in acoustic environment with or without acoustic metamaterial

由图9可以看出：在1 170～2 200 Hz频段内，声学超材料有明显的吸声效果；在1 170～1 280 Hz频段内，吸声的声压级最高可达20 dB，最小也在10 dB以上，这一频段与能带图中第1带隙的频率范围大致相吻合，此时声学超材料的振动模式为Helmholtz共振腔内空气共振；在1 300～2 200 Hz频段内，声学超材料的吸声效果良好，该频段与能带图中第2带隙和第3带隙的频率范围大致吻合，此时声学超材料的振动模式为共振腔空气与波导空气联合共振。其中：1 300～1 500 Hz频段内的吸声效果最好，声场内声压级下降了20 dB；在1 500～2 000 Hz频段内，声场内声压级下降了10 dB左右。

综上，在测试设备可测范围内，基于Helmholtz共振腔阵列的声学超材料的吸声频段宽度可达1 000 Hz，试验结果与仿真结果吻合，验证了仿真结果的准确性。

3 结论

由不同短管布置位置的Helmholtz共振腔组合成新型结构组合成新型结构，作为声学超材料的晶格，由此设计出一种带波导的基于Helmholtz共振腔阵列的声学超材料。通过COMSOL Multiphysics软件计算得到声学超材料的能带图和传递损失曲线。其中：能带图中第1带隙和第2带隙较窄，其频率范围均与传递损失峰值频段相吻合，第3带隙较宽。在第1带隙和第2带隙的频率范围内振动模式为位于晶格中间的Helmholtz共振腔体共振，在第3带隙频率范围内振动模式为Helmholtz共振腔体与周期结构形成的波导空气的共振。第1带隙、第2带隙和第3带隙下边缘均存在平直带，在平直带所属频率范围内，振动方式不随声波入射方向而改变。试验结果表明，基于Helmholtz共振腔阵列的声学超材料在1 170～2 200 Hz频段内均具有良好的吸声性能，声场内声压级下降超过10 dB，吸声频段可达1 000 Hz，适用于低频噪声的控制。

本文所设计的基于Helmholtz共振腔阵列的声学超材料为控制中低频噪声提供了新手段。