落叶松顺纹销槽承压屈服强度研究

2020-09-29杨茹元张晓凤袁权孙友富吴岳虹

林业工程学报 2020年5期

杨茹元，张晓凤，袁权，孙友富*，吴岳虹

(1.南京林业大学材料科学与工程学院，南京 210037；2.南京信息工程大学传媒与艺术学院，南京 210044)

随着低碳环保和可持续发展理念的产生及发展，木结构建筑越来越受到人们的关注[1-3]。近几十年来，北美的木结构建筑已成为低碳建筑的首选，几乎90%的低层建筑都使用木结构，如今还出现了越来越多的中高层和高层木结构建筑。节点的承载性能关系到木结构的安全性、可靠性和稳定性，是设计中极为关键的环节[4]。在各种木结构节点连接方式中，销连接是实际工程中最常用的节点连接形式。随着木结构建筑向中高层和大跨度方向的发展，销连接的应用将更加广泛。在对销连接节点进行设计时，销槽承压屈服强度是一个重要参数，对于确定节点承载性能及其可靠度的计算具有关键意义。

销槽承压屈服强度是一个系统特性[5]，受销栓直径、木材密度和含水率、荷载方向等诸多因素的影响。Rammer等[6-7]研究了阔叶材顺纹销槽承压试件的力学性能，并对3种直径的钢钉和螺栓进行了试验，结果表明，螺栓直径对销槽承压屈服刚度有显著影响，而对销槽承压屈服强度影响不大，钉径对销槽承压屈服强度和刚度均有明显影响，并提出了以木材含水率为参数的销槽承压计算公式。Sawata等[8]用4种不同直径的连接件，根据5%螺栓直径偏移法和5 mm位移最大荷载分别确定了顺纹和横纹试件的销槽承压屈服强度，结果表明，试件顺纹销槽承压屈服强度为木材顺纹抗压强度的90%，横纹销槽承压屈服强度随着连接件直径的减小而增大。Franke等[9]研究了欧洲阔叶材的销槽承压屈服强度，并比较了不同荷载方向和销栓直径对强度的影响。Schweigler等[10]研究了2种直径的连接件在不同荷载方向下对LVL(laminated veneer lumber)销槽承压屈服强度的影响，并得到了相应的力学性能。Seri等[11]重点研究了2种不同销栓直径对胶合木和规格材销槽承压屈服强度的影响，结果表明，销栓直径和制造方法对试件的销槽承压屈服强度有显著影响。Zhou等[12]和周军文等[13]研究了销栓直径对PSB(parallel strand bamboo)销槽承压屈服强度的影响，结果表明，PSB顺纹销槽承压试件呈现明显脆性破坏特征，横纹方向销槽承压屈服强度稳定且延性较好，销槽承压屈服强度与销栓直径呈反比。

当前，对我国国产落叶松在不同销栓类型和直径影响下销槽承压屈服强度的研究较少。为进一步了解国产兴安落叶松的力学性能，扩大其应用范围，笔者采用钻尾自攻螺钉和螺栓对落叶松销槽承压试件进行单调加载试验，并通过5%直径偏移法确定其销槽承压屈服强度，比较销槽承压屈服强度与销栓类型和直径的关系，最后根据试验结果，评价文献和各国规范中的理论方程对落叶松销槽承压屈服强度预测的可行性，从而为木结构销连接承载力的计算、设计提供参考。

1 材料与方法

1.1 试验材料

落叶松(Larixgmelinii)规格材产自大兴安岭，纹理通直，无病虫害，有少量活节，尺寸为40 mm×200 mm×4 000 mm，平均气干密度0.67 g/cm3，平均含水率10.84%；钻尾自攻螺钉(self-drilling screw，SDS)长100 mm，公称直径5.5 mm；螺栓等级为6.8级，公称直径分别为6，8和10 mm，分别记为M6、M8和M10。

1.2 试件制作

落叶松规格材半孔销槽承压屈服强度试验共4组60个试件，参照ASTM D5764-97a(2018)“Standard test method for evaluating dowel-bearing strength of wood and wood-based products”对试件进行加工，具体参数见表1。

表1 试件参数Table 1 Parameters of specimens

试件尺寸为50 mm(L)×50 mm(T)×38 mm(R)，其中，L为顺纹方向，T为弦向，R为径向，如图1所示。A组试件采用SDS，在实际工程中，SDS钉入木构件时通常无需预钻孔。为准确模拟SDS的销槽承压状态，将2块锯解后的小试件钻孔承压的侧面对齐贴紧，为保证槽孔位于两试件中间且垂直于试件表面，用夹具固定后，先预钻2 mm透孔，将SDS顺槽孔旋入直至穿透试件，再反方向旋出，在2块试件贴合的侧边形成相同的半孔。B、C和D组试件采用6.8级螺栓，预制槽孔时，开孔直径比螺栓公称直径大1.6 mm。选取在开孔部位无节疤、无斜纹和其他天然或加工缺陷的试件。

图1 试件尺寸示意图Fig. 1 Diagram of specimen size

1.3 试验方法

参照ASTM D5764-97a(2018)进行半孔销槽承压试验，试验装置如图2所示。采用10 t岛津力学试验机进行单调加载试验，加载速度1 mm/min。采用YHD-25型位移传感器，通过TDS-530静态数据采集系统同步采集数据，采集频率1 Hz。试验加载前将试件置于支座中心，将销栓连接件放入槽孔后对其施加荷载，由连接件传力至试件，当连接件完全被压入试件内部或者试件开裂即停止试验。试验开始前，参照GB/T 1933—2009《木材密度测定方法》、GB/T 1931—2009《木材含水率测定方法》测定木材的密度和含水率。

图2 半孔销槽承压试验示意图Fig. 2 Sketch map of half-hole pin slot embedding test

2 结果与分析

2.1 破坏形态与机理

试件主要出现3种破坏模式，如图3所示。破坏模式Ⅰ为连接件下方的木材被压溃，导致销槽孔壁变形，木材出现挤压破坏；破坏模式Ⅱ为承压面下方的木材沿木材纹理产生裂纹，主要原因是破坏区域应力过于集中，导致出现顺纹劈裂破坏；破坏模式Ⅲ为试件槽孔边缘或槽孔以外部分木材顺纹劈裂，主要原因是构件承压面边缘或其他区域受力不均匀，造成木纤维横向拉裂。所有试件会出现一种破坏模式或同时出现几种破坏模式，且随着连接件直径的增大，裂缝形式逐渐由破坏模式Ⅱ转变为破坏模式Ⅲ。

图3 试件典型破坏模式Fig. 3 Typical failure modes of specimens

试件受力时的应力状态如图4所示。当连接件开始受力时，荷载通过连接件从加载压头传递到试件上，连接件下方和应力分散边界内(图4中灰色区域)的木纤维受到压力，尤其是直接受压区域会产生明显变形。由图4可知，由于oab区域离直接受压区域较远，且超出应力边界，压力无法到达，因此该区域基本未出现破坏，这与试件破坏现象相符。随着压力的增大，bcc′b′区的垂直变形对灰色区域的木纤维产生了张力；由于竖向荷载与纤维间水平拉力的复合作用，灰色区域内的木纤维沿纹理方向产生了初始裂缝；随着压力继续增大，初始裂缝发展为贯通裂缝，试件产生破坏。

图4 试件受力时的应力状态Fig. 4 Stress state of specimen under stress

2.2 荷载-位移曲线

所有试件的荷载-位移曲线见图5。在加载初期，试件的荷载和位移近似线性关系变化；随着荷载持续增加，当达到最大荷载后，试件产生明显的顺纹开裂现象，试件破坏时其脆性破坏特征较为明显。

图5 荷载-位移曲线Fig. 5 The load-displacement curves

2.3 影响因素分析

主要数据取值方法见图6。以试件A-10为例，在荷载-位移曲线初始的线性部分拟合一条直线Ⅰ；以连接件直径5%的变形量偏移直线Ⅰ，获得直线Ⅱ；将直线Ⅱ与荷载-位移曲线交点的纵坐标作为屈服荷载(Fy)；如果直线Ⅱ与荷载-位移曲线不相交或在最大荷载之后相交，则使用最大荷载(Fmax)作为其屈服荷载，通过式(1)计算试件的屈服强度(f)：

f=Fy/(dR)

(1)

式中：d为连接件的实测直径，mm；R为试件厚度(径向尺寸)，mm。主要试验结果见表2。

图6 主要数据取值方法Fig. 6 Main data valuation method

表2 主要试验结果Table 2 The main test results

2.3.1 销栓类型的影响

图7 销栓类型与承压屈服强度的关系Fig. 7 Relationship between fastener type and embedding yield strength

销栓类型与承压屈服强度的关系见图7。由图7可知，A组SDS试件的承压屈服强度远小于其余各组，可见销栓类型对承压屈服强度有很大影响。在对理论值进行计算时，不应单纯把销栓直径作为计算参数，还应考虑销栓类型对销槽承压屈服强度的影响。

2.3.2 螺栓直径的影响

B、C和D组试件采用同一种销栓类型，以直径作为自变量，对试验结果进行方差分析，结果见表3。在α=0.05显著性水平下，螺栓直径对最大荷载和承压屈服强度影响的P值均为0.00，说明直径对最大荷载和承压屈服强度都有显著影响。

螺栓直径与最大荷载和承压屈服强度的关系见图8。由图8a可知，随着螺栓直径的增大，最大荷载也随之增大，基本呈线性关系。对螺栓直径和最大荷载的关系曲线进行线性回归分析，可得回归方程(2)，决定系数R2=0.988 5，拟合精度高。

Fmax=2.11d+2.45

(2)

表3 影响因素方差分析Table 3 Variance analysis of different factors

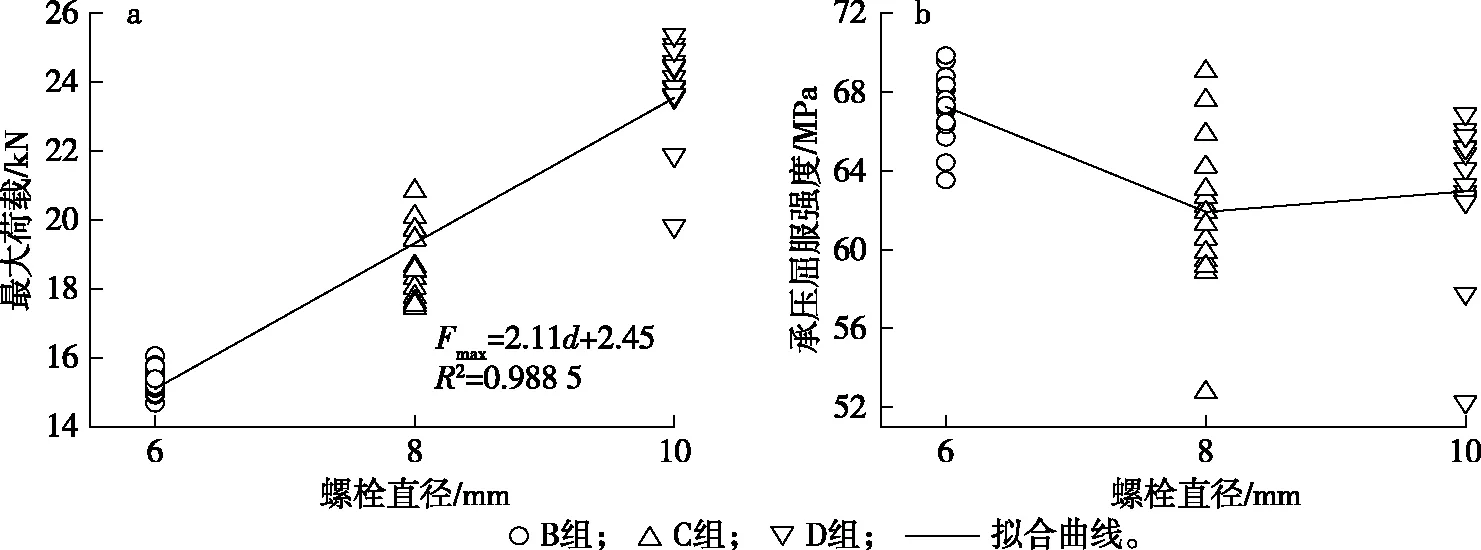
图8 螺栓直径与最大荷载和承压屈服强度的关系Fig. 8 Relationship between bolt diameters and ultimate strength, embedding yield strength

对于螺栓直径和销槽承压屈服强度关系的研究，国内外学者至今尚未得出统一结论。一部分学者认为，随着螺栓直径的增大，试件承压面积随之增加，木材更易出现天然缺陷，导致销槽承压屈服强度逐渐减小[14-15]；另一部分学者认为承压屈服强度随螺栓直径的增加而减小，但对螺栓直径较大的试样无显著影响[6]；还有一部分学者认为螺栓直径和承压屈服强度间无显著差异[16-17]。通过本研究发现，随着螺栓直径的增加，承压屈服强度呈先减小后增大的趋势(图8b)。进一步对承压屈服强度进行方差分析可以发现，在α=0.05显著性水平下，直径6 mm销栓对应的承压屈服强度与其余两组试件有显著差异(P值均为0.00)，其承压屈服强度分别是直径8和10 mm销栓对应承压屈服强度的1.08倍和1.07倍，而直径8和10 mm销栓对应的销槽承压屈服强度间无显著差异(P值为0.46)。因此，销槽承压屈服强度随着螺栓直径的增大呈减小趋势，至直径8 mm后其承压屈服强度趋于稳定。

3 顺纹销槽承压屈服强度理论值计算方法

目前对于销轴类连接件销槽承压屈服强度的计算方法很多，且主要都是基于Johansen早期提出的“欧洲屈服模式(European yield model)”[18]。通过确定不同的荷载，设计者能够根据剪切面的数量、构件的材料(木材或钢材)和销栓的长细比获得销轴类连接节点的强度。本研究总结了相关文献及标准中常用的计算方法，其中大多是基于对试验结果进行的数据拟合。

3.1 文献中的计算方法

3.1.1 Fahlbusch和Norén的计算方法

Fahlbusch[19]最初使用直径10 mm的销栓进行销槽承压屈服强度试验，并通过直径10 mm销栓的销槽承压屈服强度得到其他不同直径连接件销槽承压屈服强度，计算公式如下：

f=fd10(0.9+1/d)

(3)

式中：fd10为直径10 mm销栓的销槽承压屈服强度。

之后，Norén[20]也采用相同的计算方法得到：

f=fd10(66-d)/56

(4)

在这2个表达式中，销槽承压屈服强度与销栓直径成反比。与Norén的计算方法相比，Fahlbusch提出的公式中系数较小，但这2个公式中都没有与木材特性有关的参数。

3.1.2 Ehlbeck的计算方法

Ehlbeck等[21]提出了一个基于针叶材和阔叶材销槽承压试验的拟合公式，其中，销槽承压屈服强度与木材密度成正比，根据销栓直径进行轻微修正后可得：

f=0.102(1-0.01d)ρ

(5)

式中：ρ为木材气干密度平均值。

此公式结构与欧洲木结构设计规范EC5(BSEN 1995-1-1:2004+A2:2014“Eurocode 5: Design of timber structures-Part 1-1: General-Common rules and rules for buildings”)中的公式结构非常相似。Ehlbeck等[20]指出，在节点受力时，槽孔下方木材的受力区域随着销栓直径的增加而增大，因此在公式中将销栓直径作为一个次要参数进行考虑。

3.2 现行标准中的计算方法

3.2.1 欧洲木结构设计规范

目前对销轴类连接件进行计算时，最常用的是欧洲木结构设计规范EC5中规定的计算方法。EC5中对销槽承压屈服强度的计算主要来源于Whale等[22-23]早期的研究，他们主要对欧洲的针叶材和一些热带阔叶材进行了销槽承压试验，并拟合出计算公式。与大多数此类公式一样，销槽承压屈服强度主要与木材密度有关，销栓直径对其影响较小。不同的是EC5对不同销轴类型的计算方法进行了区分，其中，式(6)为钉销槽承压屈服强度计算方法，式(7)为螺栓销槽承压屈服强度计算方法：

(6)

f=0.082(1-0.01db)ρk

(7)

式中：ρk为木材气干密度5%分位值，ρk=ρ×(1-1.65×10%)；dn为钉的直径；db为螺栓直径。

3.2.2 美国木结构设计规范

美国木材委员会根据Wilkinson[24]进行的针叶材销槽承压屈服强度试验提出了一个简单的公式，最初Wilkinson的计算方法忽略了销栓直径对销槽承压屈服强度的影响，最新的NDS(national design specification)规范对这一计算方法进行了调整，划分了不同的直径范围，计算公式为：

f=77.22G,d<6.35 mm

(8)

f=114.45G1.84, 6.35 mm≤d≤25.4 mm

(9)

式中：G为木材全干相对密度。

3.2.3 我国木结构设计标准

我国最新的GB/T 50005—2017《木结构设计标准》参照了NDS中的计算方法，计算公式为：

f=77G,d<6 mm

(10)

f=115G1.84, 6 mm≤d≤25 mm

(11)

综上所述，大多数理论值的计算方法都来源于对试验数据的拟合，这些计算方法大多是简单的线性回归模型，仅少数计算方法使用了简单的非线性表达式。所需计算参数中，主要参数为木材密度，次要参数为销栓直径。

不同销槽承压屈服强度计算方法比较见图9。根据材性测试结果得到每组试件的气干密度平均值，木材全干密度(ρ0)参照ASTM D2395-17“Standard test methods for density and specific gravity(relative density) of wood and wood-based materials”换算，按式(12)进行计算：

ρ0=ρ/(1-0.009ρW)

(12)

式中，W为木材含水率。本试验中试件平均含水率为10.84%，根据式(12)得到木材全干相对密度G=0.72。不同销槽承压屈服强度计算方法比较如图9所示。

图9 不同销槽承压屈服强度计算方法比较Fig. 9 Comparison of calculation methods for embedding yield strength of different pin slots

落叶松顺纹销槽承压屈服强度模拟计算结果及相关系数见表4，各组试件理论值与试验值的相关性比较见图10。对于相关文献的计算结果，文献[19]的计算方法误差最小，误差范围为0.13%～4.68%，原因是计算时使用了直径10 mm螺栓的销槽承压屈服强度作为计算参数，但在实际设计时，获取这一参数较为复杂，所以此计算方法并不实用。