木粉爆炸最大压力预测模型的修正

2020-09-29胡涛平喻孜郭露徐长妍

林业工程学报 2020年5期

胡涛平，喻孜*，郭露，徐长妍

(1. 南京林业大学理学院，南京 210037； 2. 南京林业大学材料科学与工程学院，南京 210037)

在粉体的制造、处理以及有粉尘的生产工业中，当粉体或粉尘分散悬浮在空气中，并且有足够能量的点火源时，就可能会发生爆炸[1-2]。粉尘爆炸过程中，火焰在粉尘云中快速传播，同时温度和压力也会迅速升高。在有限空间内，粉尘爆炸快速释放巨大的能量和超强的冲击波，具有很大的破坏性和危害性[3-4]。

为防止或减轻粉尘爆炸造成的财产损失和人员伤亡，许多学者已通过试验研究了粉尘爆炸的物理化学性质，如最小点火能、最低点火温度、最大爆炸压力、最大压力上升速率以及爆炸时产生的能量等[5-8]。除试验研究，理论上研究粉尘爆炸的动力学演化模型，可以探究粉尘爆炸机理。利用理论模型数值仿真计算试验数据，可对粉尘燃爆的危害等级进行预测，以便确定爆炸的严重性[9-12]。马汉翔等[13]采用线性回归方程理论计算了20 L爆炸球中梧桐树粉尘爆炸试验数据，研究了粉尘浓度、点火能以及粉尘粒径对爆炸压力的影响。然而，他们是根据方差分析模型得到多元二次回归方程的数学建模，并未讨论粉尘爆炸的物理机制及模型。Rahman等[14]理论预测了最大爆炸压力上升速率以及层流的燃烧速率，主要是利用火焰传播机理研究爆炸中火焰的燃烧特性。Callé等[15]根据20 L爆炸球试验，提出爆炸过程中压力演化的动力学模型，研究了木粉浓度与粒径对木粉爆炸的影响。然而，在Callé等的木粉燃爆模型中，忽略了爆炸过程中还未燃烧的木粉对爆炸反应的吸热效应，他们认为木粉的导热系数很低，因此忽略了其吸热。但是，根据粉尘爆炸机理以及理想气体物态方程，气体温度升高导致爆炸压力上升，而由热力学原理，气体温度升高是源于爆炸产生的热量被气体吸收。因此，若忽略爆炸进程中未燃烧木粉应该吸收的热量，则必然会将这部分热量计算为气体的吸热，从而使计算得到的温度增量大于试验实际值，致使计算得到的压力也高于试验测量值。这就是导致Callé模型最大爆炸压力计算值与试验测量数据产生较大偏离的原因。在升温过程中，表征材料吸热的物理量是热容。在标准状态下，纤维素的热容为320～440 J/(kg·K)，与空气热容的比值约为1∶3。因此，在计算木粉爆炸压力时，不可忽视未燃烧木粉的吸热。

研发木质粉尘燃爆防控技术和装备是实现行业安全生产的重要措施，而构建准确的木质粉尘燃爆参数预测模型则是该防控技术研发的基础。笔者基于热力学基本定律以及燃烧反应动力学，推导出木粉燃爆中最大爆炸压力计算的理论模型，并理论仿真计算了燃爆试验数据，研究结果对木质粉尘燃爆防控构件及相关技术的研发具有重要的理论意义。

1 木粉燃爆理论模型

组成木材细胞壁的物质决定了木材的主要物理性质，而木材细胞壁的主要成分是纤维素。因此，以纤维素(C6H10O5)代表木材。

在燃烧化学反应中，纤维素完全燃烧的产物是CO2和H2O，化学反应式为：

C6H10O5+6O2+24N2→6CO2+5H2O+24N2

(1)

在20 L爆炸球内，纤维素的燃烧化学反应平衡可表示为[15]：

(2)

式中：X为燃烧转化率(燃烧消耗量和初始燃烧数量的比值)；r为反应速率；V为反应体系的体积；νC,0为初始时刻纤维素的物质的量。按照式(1)，根据燃烧的反应平衡，假定初始时刻氧气的物质的量为νO2,0，则t时刻纤维素和氧气的物质的量变为νC,0(1-X)和νO2,0-6XνC,0，t时刻CO2和H2O的物质的量分别为6XνC,0和5XνC,0。化简式(2)可得：

(3)

其中，r的定义[15]为：

(4)

式中：k为反应速率常量；ρC6H10O5和ρO2分别为纤维素和氧气的浓度。根据过渡态理论以及分子碰撞理论，可推导出燃烧反应中k与温度(T)的关系为：

(5)

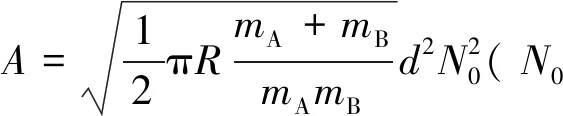
燃爆中，气体的总物质的量ν由反应平衡计算：

ν=νO2+νCO2+νH2O+νN2=νO2,0+νN2,0+5XνC,0

(6)

式中：νO2、νCO2、νH2O分别为O2、CO2和H2O的物质的量；νN2,0为初始时刻N2的物质的量。

对于一个热力学系统，其焓(H)的定义为：

H=U+pV

(7)

式中，U和p分别为系统的内能和压强。对式(7)两边进行微分可得：

ΔH-Δ(pV)=ΔU

(8)

再根据理想气体物态方程pV=νRT可得：

Δ(pV)=νRΔT+RTΔν

(9)

将式(9)代入式(8)，并利用理想气体内能公式U=νCVT可得(推导过程中用到了关系式Cp=CV+R)：

ΔH-RTΔν=ν(CV+R)ΔT=νCpΔT

(10)

式中：Cp为各种气体的定压摩尔热容；CV为各种气体定体摩尔热容。

20 L球内的热平衡为：

(11)

式中：ΔHr为1 mol可燃物的反应热；i为球内的气体成分和木粉。

(12)

式中：j为燃烧产物；ΔHr,0=ΔHr(0)是在0 K、1个标准大气压下可燃物的燃烧热。与温度相关的Cp表达式为Cp=a1+b1T+c1T2+d1T3，其中，参数a1、b1、c1、d1的取值如表1所示。

表1 Cp表达式中的参数Table 1 Parameters in the Cp expression

2 理论计算分析

给定初始条件，对式(2)～(12)迭代计算，木粉燃爆压力可由理想气体物态方程pV=νRT和道尔顿分压定律仿真计算得到。即利用爆炸反应的热平衡式，用燃烧反应放热减去未燃烧木粉的吸热，可计算得到气体吸热值以及由于吸热导致的温度上升，从而根据理想气体物态方程计算对应的爆炸压力。计算爆炸过程中球内不同时刻爆炸压力时，可得球内爆炸压力(P)随时间变化的曲线图。

爆炸期间25～45 μm粒径的木粉爆炸压力试验数据见图1[15]。图1中，木粉的质量为2.6～40.9 g，不同的木粉质量即代表不同的木粉浓度。

图1 爆炸压力试验数据Fig. 1 Experimental data of explosion pressure

本模型和Callé模型的理论仿真计算与试验数据的拟合曲线如图2所示，其中，EA=9 kJ/mol。由图2可知，Callé模型只模拟计算了5.1～20.3 g的4组不同质量木粉的试验数据，根据4条模拟曲线可知，Callé模型的拟合结果只是对试验数据大致趋势的拟合，最大爆炸压力计算与试验测量结果偏离较大。而本研究理论模型的拟合曲线与试验数据高度吻合，燃爆的最大爆炸压力理论值非常接近试验数据。此外，Callé模型缺乏3组试验数据的理论计算，而利用本研究模型对此3组试验数据的拟合度同样较高。本研究对所有7种不同质量木粉的理论拟合结果表明，最大爆炸压力随着木粉质量的增加而先增大后减小，在14.6 g出现极大值，与试验结果完全一致，较好地诠释了试验现象。

注：对应符号的虚线为已有模型的拟合曲线；实线为本研究理论模型的拟合曲线。图2 理论模型计算数据与试验数据拟合Fig. 2 Theoretical model calculated data and experimental data fitting

为了更清楚地看到本研究理论模型对试验数据的拟合效果，不同木粉质量下本研究模型模拟计算的最大爆炸压力见表2，并与Callé模型进行了对比。从表2可以看出，与Callé模型理论计算的4组质量(5.1～20.3 g)相比，本模型的拟合结果除了在5.1 g时与试验值偏差稍大，在8.5，14.6和20.3 g 这3组质量下的拟合偏差均不高于1.0%，最小拟合偏差仅为0.1%，而Callé模型的拟合偏差为15%～24%，与试验结果相差较大。因此，在共同模拟的4组木粉质量下，本研究模型极大提高了理论计算值与试验数据的拟合度。此外，Callé模型并未对另外3组木粉质量(2.6，29.6和40.9 g)的试验数据进行模拟计算，而本研究模型对此3组木粉质量的拟合结果表明，理论值与试验值的平均偏差为1.3%左右，对试验数据进行了很好的理论诠释，弥补了已有模型的不足。

表2 不同质量木粉对应的最大爆炸压力试验值与理论值Table 2 Experimental and theoretical value of the maximum explosion pressure of different wood powder masses

图3 最大爆炸压力随木粉质量的变化Fig. 3 The maximum explosion pressure changing with different wood powder masses

利用理论模型，拟合了木粉质量连续变化下的最大爆炸压力曲线，如图3所示。除了木粉质量为5.1 g，其他6种木粉质量时曲线的理论值与试验数据高度贴合，进一步表明本理论模型的优势。最大爆炸压力先随木粉质量的增加而上升，在到达极大值后，再随质量的增加而下降。试验数据表明，最大爆炸压力极大值出现在木粉质量为14.6 g时，极大值为0.757 MPa。理论计算曲线结果显示，最大爆炸压力极大值出现在木粉质量为12.5 g附近，极大值为0.768 MPa。由于试验测量时一般是选取某些间断的质量值，不可能无限小质量间隔进行连续质量选取，而理论模型可以通过对连续质量进行计算。因此，本模型可以预估给定木粉质量时的最大爆炸压力，为燃爆的防控提供理论依据。