改进粒子群算法优化最小二乘支持向量机的高炉炉温预测研究

◎薛永杰

（作者单位：青岛科技大学）

一、引言

高炉炼铁是一个复杂的多变量控制系统，保证炉内状况稳定很有必要。其中炉温的控制是十分重要的因素。良好的炉温控制是高炉生产稳定的前提。本文提出了一种基于粒子群算法优化最小二乘支持向量机的高炉炉温预测模型。首先建立具有径向基函数为核函数的最小二乘支持向量机模型，将最小二乘支持向量机参数作为粒子初始位置，然后通过粒子群信息交流找到最优参数，并通过改进粒子群算法优化惯性权重和学习因子，得到采用最优参数的最小二乘支持向量机建立的高炉炉温预测模型。实验结果表明，本文模型提高了高炉炉温的预测精度，并大幅减少训练时间。

二、IPSO－LSSVM 的高炉炉温预测模型

1.最小二乘支持向量回归模型。

LSSVM 的基本原理为，给定非线性训练样本集T，T= {（xi，yi）i=1，2，…，n}，x∈Rn的子集表示输入数据，yi∈Rn 的子集表示输出数据，n 表示样本训练个数。映射非线性函数以获得高维特征空间。进行线性回归分析。基于结构风险最小化原理，得到LSSVM 的优化目标函数。为了解决最优问题，引入拉格朗日乘数，将约束下的优化方程转化为无约束目标函数。依据KKT 优化条件得到最优值。然后得到最小二乘支持向量机分类决策函数。大量研究实验表明高斯径向基核函数可以获得良好的性能。因此本文采用高斯径向基核函数来帮助LSSVM 预测模型获得最优解。

2.改进粒子群算法。

假设在d 维的搜索空间内，有n 个粒子组成的一个种群，χi表示第i 个粒子的位置，νi表示第i 个粒子的速度，pi表示粒子搜索的最优位置，pg表示种群搜索的最优位置。粒子更新速度与位置的公式为（1）（2）：

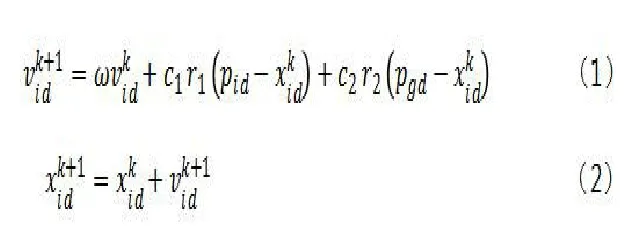
式中k 表示实验中迭代的次数，c1和c2为学习因子，ω 为惯性权重系数，r1和r2为[0，1]内的随机函数。惯性权重ω 用于平衡全局搜索与局部搜索能力，可以通过以下公式（3）确定：

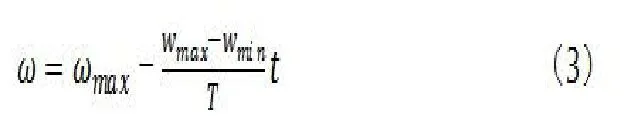
式中Wmax 是初始权重，Wmin 是最终权重。T 为最大迭代次数。由于标准PSO算法收敛快，实际应用中容易陷入局部最优，使寻优陷入停滞。为了提高算法的收敛性和提高运算效率。提出了一种种群多样性粒子群算法，算法提出了“吸引”和“扩散”的概念，动态的调整求解过程，公式（4）如下：

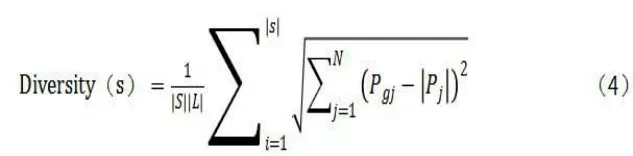
式中为│s│种群大小，│L│为搜索样本空间的最长半径。在算法搜索过程中，当Diversity(s)＜DLOW时，种群中粒子远离最优位置，执行扩散操作。Diversity(s)＞Dhigh时，种群中粒子向全局最优位置靠拢，执行吸引操作。通过对种群粒子速度的动态调整，在达到一定精度后，继续寻找最优解，以保证寻找到的结果为最优结果。

3.改进粒子群算法优化最小二乘支持向量机。

IPSO 优化LSSVM 模型实现高炉炉温预测的算法步骤如下：

1.对数据进行预处理。

2.根据模型的预测误差计算每一个粒子的适应度函数值。

3.设置IPSO 参数的初始值。

4.计算粒子群适应度。

5.判断适应度。如果满足则终止参数寻优，如果不满足则返回步骤（4）。

6.根据最优参数和。

三、实验结果与分析

本文选用山东某钢铁厂3 号高炉2017 年7 月到9 月日常生产中的1195 组数据，选用影响高炉炉温的决策变量、条件变量和目标变量，删除无关变量，整合成初始样本集根据相关性分析，选择6 个参数作为输入层神经元，隐含层为13 层，隐含层的作用输出函数采用tansig 型，本文章研究的是高炉炉温的预测，故输出变量为当前高炉炉温，所以输出神经元个数为1。共得到876 个样本，其中前776 个样本作为训练集，后100 个样本作为测试集。分别采用GA、PSO 和IPSO 算法对LSSVM 模型参数寻优，得到他们选择的最优参数，利用得到的最优参数让LSSVM 进行学习，建立相应的高炉炉温预测模型。预测性能好坏通过MAE、MAPE、RMSE 及模型的运行时间对比得到，对比结果如表1 所示

?

相 比 于 GA-LSSVM 模 型 和PSO-LSSVM 模型，IPSO-LSSVM 模型预测炉温精度更高，建模时间更短。

四、结束

本文结合高炉冶炼生产过程的特点，为了提高高炉炉温预测性能，在筛选优化样本数据的基础上，运用改进粒子群算法优化最小二乘支持向量机建立高炉炉温预测模型。并和GA-LSSVM、PSO-LSSVM 预测模型对比实验。实验结果表明，本方法较全面考虑了高炉炉温变化的因素，而且训练速度快、运行效率高等特点，同时也提高了模型预测精度和命中率。在以后的研究中，可以尝试加入更多的输入变量，采用更好的算法优化模型，得到更好的预测结果。