多尺度自相似融合图像超分辨率重建
2020-09-29刘志坚
刘志坚,张 刚
(江苏建筑职业技术学院 建筑智能学院,江苏 徐州 221000)
图像超分辨率重建技术是对低分辨率图像进行一系列运算后获得高分辨率图像的技术。利用该技术可以降低图像采集设备的成本,因而成为图像处理技术的研究热点之一[1-2]。
为提高图像重建的效果和速度,本文提出多尺度自相似融合图像超分重建算法(MS-SANR)。该算法采用分层搜索匹配策略进行低分图像与锚点的搜索匹配。首先将图像进行小波分解,获得不同尺度的小波域图像;再在ANR 方法的基础上引入自相似正则化矩阵;最后通过构建的多尺度串联模型对图像进行重建。
1 关于超分辨率重建的研究
超分辨率重建是一个病态问题,当前进行超分辨率重建的主要方法是通过对大量样本图像进行直觉性理解或统计分析以获得图像的先验知识[3-4],以及寻找合适模糊核的方法[5-6]。这2 种方法都是对较小的图像块进行操作,通过对多个图像块进行线性或非线性运算获得有效的局域先验信息。例如求取重叠图像块的平均值或利用置信传播和图分割方法获得最大后验概率的图像块运算[7]。文献[8]提出SISR 方法,利用大量高低分辨率样本图像训练得到稀疏字典,并利用稀疏编码和稀疏字典重建高分辨率图像的细节信息;文献[9]提出利用K-SVD 方法学习稀疏字典并利用正交匹配追踪(OMP)算法进行稀疏运算,在重建效率上很好地改进了SISR 方法[9]。
但是,先验信息的有效性是以大量训练图像集为基础,这也使有限的内存和时间复杂度制约着该类算法的实际应用。领域嵌入方法假设低高分辨率图像具有相似结构的流形学习,故高分辨率图像可以通过低分辨率图像与最近邻的流行结构进行估计[10-11]。文献[12]提出ANR 方法,将SISR 和改进的SISR 方法中图像块的稀疏分解优化问题转化为岭回归问题,并离线处理和存储,大大降低了重建时间复杂度;文献[13]提出A+方法,是在ANR 方法基础上对回归模型的训练样本进行优化,进一步提高了重建图像质量。近期,基于卷积神经网络的超分辨率重建方法也开始被陆续提出,文献[14]提出的SRCNN 方法通过卷积神经网络直接学习高低分辨率图像的映射关系。
2 基于稀疏编码的超分辨率重建方法
图像超分辨率重建是利用已知的先验信息或数学模型计算获得降质前的高分辨率图像;而图像降质过程与重建过程相反,其数学模型可以表示为:

式中:S 表示下采样过程,H 表示模糊过程,n 表示白噪声。由式(1)可知,超分辨图像重建是已知低维数据而计算高维数据的过程。
文献[8]提出的稀疏编码模型中,通过大量的样本图像学习获得稀疏表示字典Dl,低分辨率图像块可以进行重建:

式中:F 为特征提取矩阵,α为稀疏表示系数,y 为输入的低分辨率图像块,λ 是权重参数。
由于l0-范式是一个NP 难问题,所以可以转化为l1-范式进行求解[15-17]:

而为了得到高分辨率图像块Xh和低分辨率图像块Yl相同的稀疏表示,高低分字典Dh和Dl可以采用联合训练的方式进行计算:
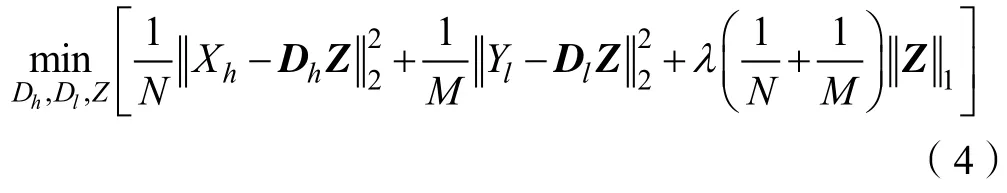
式中:M 和N 分别表示低分辨率块和高分辨块的维数,Z 表示稀疏约束的系数向量。
根据已知的低分辨率块可以求得稀疏表示系数Z,所以高分图像块可通过下式计算获得:

3 多尺度自相似融合图像超分辨率重建
3.1 算法框架
为了提高图像边缘和细节信息准确性,减少重建误差,在ANR 方法的基础上引入自相似矩阵(SANR)。因为小波域能够更好地保留图像边缘信息,所以利用小波分解构建多尺度串联(MS)算法框架,实现不同尺度图像分层多次重建,因而显著削弱了阶梯效应,使图像重建效果更好。
此外,在重建过程中增加了字典原子数和邻域数,提出分层的搜索匹配方法进行低分辨率图像块对应的锚点匹配,以减少图像重建编码时间,其算法框架如图1 所示。

图1 算法框架
3.2 自相似矩阵
定义字典原子dj的邻域Nj为字典中K 个最相关的原子,即与dj内积最大的K 个原子,dj为邻域Nj的锚点。利用文献[9]提出的方法训练获得高低分辨率字典DhDl后,计算每个原子的邻域。对于稀疏编码方法,最小二乘问题使用系数的l1-范式进行约束[17]。而为了进一步简化计算,可以转化为使用系数的l2-范式进行约束的最小二乘回归问题[18]:

式中:yF为低分辨率特征图。根据(4)可计算高分辨率图像块x:
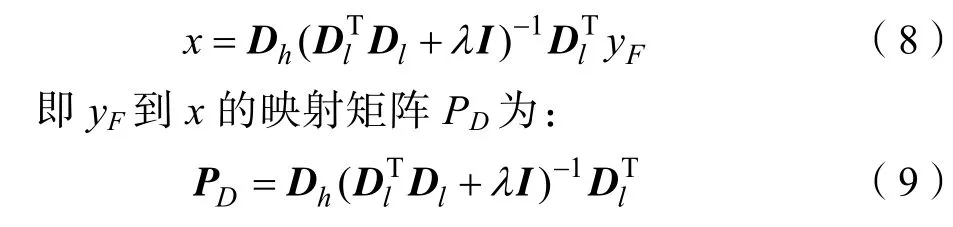
采用局部邻域Nl和Nh替换字典Dh和Dl,则字典原子dj对应的映射矩阵PNj
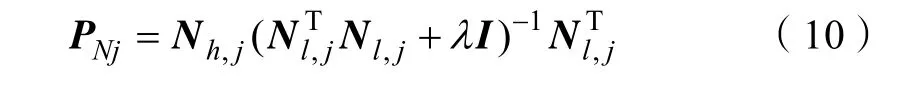
高分辨率图像块xj的估计矩阵为:

在重建过程中,若使用l2-范式进行约束,则会增强图像纹理的重影和平坦区域的阶梯现象。为此,增加自相似融合矩阵Ej使估计矩阵更准确。令si,j=yi,jyj, sj= [ s1,j, s2,j, … , sk,j]T,yi,j是低分辨率图像块yj的第i 个最相似图像块,相似度采用内积计算,k 取32。则高分辨率图像块xj的估计矩阵为:

由于图像中每个图像块可以由若干与之相似的图像块线性运算,得到其近似估计图像块[19],所以图像块差值也可由其他与之相似图像块差值线性运算获得:

式中:wi为系数,利用最小二乘法求解公式(14),即可求解 Ej= [ w1, w2, …, wk]。
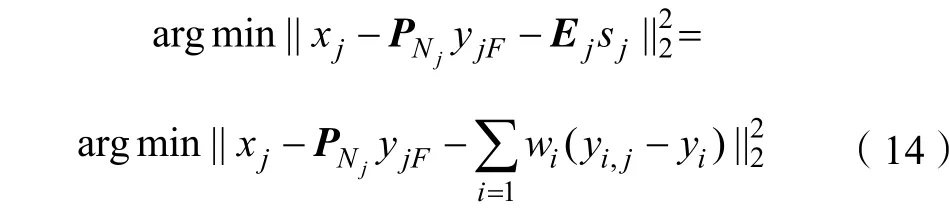
3.3 多尺度串联框架
图像纹理复杂多样,且受噪声影响。小波分析具有高低频信号分离处理的特点,能够在不损失原有重要信息的前提下对图像进行噪声滤波处理,并重构出原信号。此外,小波分析能够对原信号进行多分辨率特征分析,较合理地分配计算成本,兼顾不同尺度下信号特征的差异性。根据文献[20],图像进行多次超分重建的效果优于单次超分重建的效果,所以本文提出多尺度串联框架,如图2 所示。

图2 多尺度串联框架
按照多尺度串联框架,先对图像进行小波3 层分解。考虑到小波分解层次越深,小波分量维度越小,所以对每层分量,根据信号尺度采用不同长度的SANR 方法串联,进行多次重建,前SANR 重建结果作为后SANR 的输入图像。图2 中,其中Hi、Vi和Di是第i 层小波分解的水平、垂直和对角方向获得的信号分量,SANR 方法串联长度为i,构成i 层SANR。最后,对重建后的高频分量和原低频分量进行小波重构。
3.4 分层搜索匹配算法
在使用基于字典学习的算法进行图像高分辨率重建时,字典越大,则重建模型性能会越好;而SANR方法作为一种以字典学习为基础改进而来的方法,在搜索匹配原子邻域时,其计算复杂度也与待搜索的邻域数相关。为了提高原子邻域搜索效率,笔者提出分层搜索匹配算法。假设有N 个邻域和邻域锚点,该算法步骤如下:
(1)首先使用聚类算法对N 个邻域锚点进行聚类,本文使用K-means 聚类算法,簇数为;
由于在ANR 和SANR 中,采用线性查找方法进行低分辨率图像特征块特征匹配和搜索邻域时,时间复杂度为 O( N),即搜索时间随着邻域数量而呈线性增加;而分层搜索匹配算法是根据所有邻域的锚点进行多层分类搜索匹配,时间复杂度为 O()。
4 实验分析
为了验证MS-SANR 算法的性能,在Matlab 2014平台(Windows 7,RAM 8 GB)上进行了仿真实验,并与Bicubic(双三次插值)算法、SISR 算法、K-SVD算法和ANR 算法进行比较。实验中,字典训练采用K-SVD 算法和图像训练集,字典原子数为1024。K=128,λ=0.01,重建尺度因子为 3,测试图像来自SET5[12]标准图像集,本文仅以头像(280×280)和鸟(288×288)两幅图像(见图3)为例进行比较。

图3 SET5 测试图像
采用峰值信噪比(PSNR)和重建编码时间这2 个客观参数对不同算法进行评价,重建结果如图4、图5和表1、表2 所示。每幅测试图像的重建结果中第一行为全幅图像结果,第二行为对应重建图像中的局部图像。从重建结果中可以看到,MS-SANR 算法对于细节重建比其他几种方法效果更好,例如图4 中人物皮肤上的斑点更清晰,图5 中的纹理边界也比其他算法更清晰,边缘重影现象削弱。此外,在图像重建时,YSISR 和K-SVD 两种算法的重建结果存在一定的阶梯效应,而MS-SANR 算法以因采用小波变换和增加自相似融合矩阵的方法,较好地削弱了阶梯效应。
从表1 中可知,各图像重建结果的PSNR 均有提高,平均提高1 dB。因此,MS-SANR 算法无论是在主观评价还是在PSNR 客观评价中都表现出更好的图像重建效果。表2 记录了各算法重建阶段的编码时间。MS-SANR 算法采用的邻域数为32 768,而ANR 算法采用的邻域数为1 024。但从表2 中可知,MS-SANR算法的重建编码时间相比其他方法略有减少。当图像较大时,编码时间减少的优势将更显著。这显现了分层匹配策略对提高算法效率的有效性。
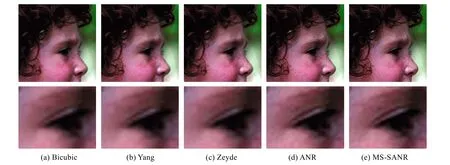
图4 测试图——头像

图5 测试图——鸟
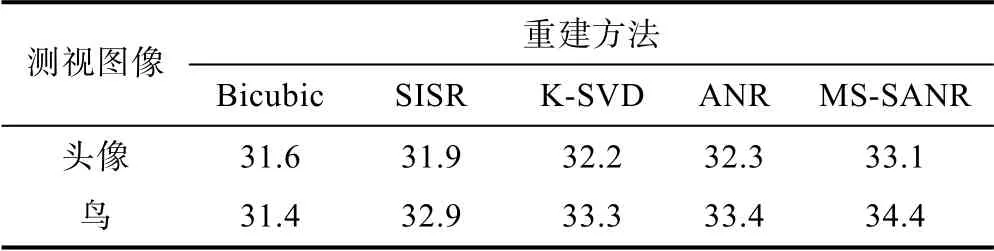
表1 不同超分辨率重建方法的PSNR(dB)结果

表2 不同超分辨率重建方法编码时间 s
5 结论
本文在基于ANR 的图像超分辨率重建基础上提出的多尺度自相似融合图像超分辨率重建算法,增加了自相似矩阵,使重建图像的细节部分更加清晰,削弱了图像边缘的重影现象和阶梯效应,提高了重建图像的峰值信噪比。
