Mrk 421天体的多波段辐射机制*

谢星星, 康世举, 刘文广

(1.云南师范大学 物理与电子信息学院,云南 昆明650092；2.六盘水师范学院 物理与电气工程学院,贵州 六盘水 553004)

耀变体是活动星系核的一个极端子类，其多波段能谱分布(The Spectral Energy Distribution,SED)包括两个明显的连续成分，对应两个光滑的峰.低能峰位于射电到紫外波段，甚至软X射线波段之间，高能峰位于硬X射线到TeV伽马射线波段之间[1].两个峰对应着不同的辐射机制，一般认为，低能峰是由耀变体喷流中加速的非热电子的同步辐射产生，高能峰主要是轻子起源[2]，而极端高能成分的辐射能谱可能是强子起源.

由于观测受限，耀变体的SED无法直接得到，但是对于耀变体而言，假设了非热相对论性电子能量分布之后，便可以使用相应的模型来拟合耀变体的SED[3-4]，进而反演耀变体喷流中的物理特性，Markarian 421(Mrk 421)是高能伽马射线实验望远镜(Energetic Gamma Ray Experiment Telescope,EGRET)首次探测到的100 MeV以上的BL Lac天体，Chen等人[3]直接假设了电子能量分布，使用同步自康普顿(Synchrotron-Self-Compton,SSC)模型计算了Mrk 421天体的SED，但是没有讨论电子在激波上游的注入、加速以及下游辐射区的冷却.Zheng等人[5]假设低能电子在激波上游注入并加速，得到的电子谱具有两段不同的能量分布，而以往的研究中电子在激波上游所形成的电子谱仅具有一段分布[6].为了探究这种特殊的两段式电子谱在激波下游经历辐射冷却过程后能否通过模型计算出Mrk 421天体的SED，本文基于该假设[5]，利用激波的边界条件，在激波下游辐射区得到了一种新的电子能量分布.其次利用新的电子能量分布，基于SSC模型计算了Mrk 421天体四个时期的多波段能谱分布，并对模型计算结果进行了讨论.文中取哈勃常数H0=75 km/(s-1·Mpc-1)，物质能量密度ΩM=0.27，辐射能量密度Ωr=0，无量纲宇宙学常数ΩΛ=0.73.

1 电子能量分布

考虑激波沿柱形喷流传播，电子在激波上游被加速，随后漂移到激波下游区域，上述过程可以看作存在两个空间区域：一个是激波上游的加速区，电子在加速区被不断加速而获得能量；另一个是激波下游的能量耗散区，电子在能量耗散区由于辐射冷却释放出大量的能量[7].假设两个区域都存在随机起源的均匀磁场且充满均匀分布的相对论性电子，如果电子在激波上游被注入和加速，可以获得激波上游的电子谱[5]

(1)

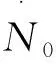
(2)

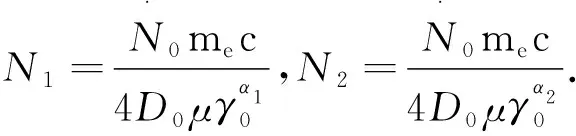
假设激波上游与下游的界面存在适当的边界条件，被加速过的电子N0(γ,γ0)快速地漂移到下游区域.可以通过洛伦兹因子γ来演化激波面附近的电子分布[6，8]，演化方程

(3)

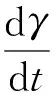
(4)

2 同步自康普顿模型

SSC模型认为逆康普顿散射中的软光子来源于喷流中电子的同步辐射，该模型被广泛用于解释耀变体的辐射能谱，其范围从射电波段延伸到X射线波段，甚至是高能射线波段.Zheng等人[5]对模型进行了详细的研究和解释，在此仅对模型进行简单描述.

SSC模型假设存在一个带有非热相对论电子的球形辐射区，通过求解球对称结构辐射转移方程，根据Kataoka[10]和Zheng[5]的研究方法得到同步辐射的辐射强度Isyn(ν)，进而推导出逆康普顿散射强度Iic(ν).球形辐射区以ν=βc的速度相对观测者移动，由于多普勒聚束效应放大了观测到的辐射，通过对辐射强度进行修正，获得地球上观测到的辐射流量

(5)

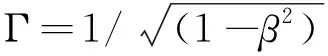
3 模型的应用

设定式(4)中的归一化系数K1=κN1tesc，K2=K1×γ0(α1-α2)，当γc满足关系式γmin≤γc<γ0时，式(4)可以改写为

(6)

利用式(6)描述的电子能量分布，基于SSC模型来拟合Mrk 421天体在MJD 56302、MJD 56307、MJD 56312和MJD 56335四个时期的观测数据(数据来自Swift-UVOT,Swift-XRT,NuSTAR,Fermi-LAT,MAGIC和VERITAS收集到的同时性观测)[13]，拟合结果如图1所示(黑色实心方块为多波段的观测结果，黑色点虚线是γ<γ0时的辐射能谱，黑色长虚线是γ>γ0时的辐射能谱，黑色实线是叠加的总能谱).图2给出了Mrk 421四个时期的SED所对应的电子能量分布(点划线表示γmin≤γ<γ0的电子能量分布，点虚线表示γc≤γ<γmax的电子能量分布，黑色实线表示叠加的总电子能量分布).

图1 拟合的SED与Mrk 421四个时期的观测数据对比图

图2 Mrk 421四个观测时期的SED所对应的电子能量分布

表1 Mrk 421的模型参数

表1中给出了Mrk 421的模型参数，谱指数α1的大小为2.47±0.04，α2的大小为-1.9±0.21，Cerutti等人[14]讨论了高能幂律谱指数的区间为α∈[-3,-2]，拟合得到的高能部分的电子谱指数α2与该范围较为接近.多普勒因子δ的大小与Abdo等人[15]使用轻子模型拟合Mrk 421的数据得到的结果δ=21较为接近，得到的R与Abdo等人计算的辐射区域半径(R=5.2×1016cm)在量级上是一致的.拟合结果表明γ0偏小，式(1)所采用的电子谱是在假设低能粒子注入的情况下得到的，所以较低数值的γ0也符合Zheng等人[5]对式(1)的假设.综上所述，拟合Mrk 421四个时期的SED所得到的模型参数是较为合理的.

基于图1和图2的结果，发现电子分布的低能部分对辐射能谱几乎没有贡献.由Mrk 421的模型参数可以看出，四个时期的电子谱指数α1的数值相差不大，它是电子分布低能部分的谱指数，对辐射能谱的形状影响较小；四个时期的α2数值相差较大，由于它是电子分布高能部分的电子谱指数，电子能量较高导致对辐射能谱的贡献较大.改变α2的数值可以导致X射线波段的辐射能谱的改变.电子漂移到激波下游辐射区，经历了辐射冷却和逃逸过程损失能量并形成电子能量分布，γc作为电子辐射冷却和逃逸的临界洛伦兹因子，电子洛伦兹因子小于临界洛伦兹因子时，电子以逃逸损失为主，电子洛伦兹因子大于临界洛伦兹因子，辐射冷却主导能量损失过程，所以这个临界点的大小是改变电子分布的关键点.γc的变化影响了电子能量分布的形成过程，进而对辐射过程产生了影响.因此，推测电子分布的高能部分对辐射能谱的贡献和电子能量损失过程中临界能量的改变都是导致Mrk 421天体的能谱变化的原因.

4 结 语

虽然Mrk 421的多波段能谱已被长期研究，但喷流的性质、伽马射线发射的位置和发射机理仍不清楚.一般情况下通过不同的辐射机制可以得到不同的电子分布.在激波下游我们得到了γmin≤γc<γ0的电子能量分布;基于SSC模型，使用电子能量分布对Mrk 421在MJD 56302、MJD 56307、MJD 56312和MJD 56335四个时期的观测数据进行了拟合.根据拟合结果，发现电子分布的低能部分对辐射能谱几乎没有贡献，可能是低能电子的冷却时标较长导致的.电子分布的高能部分对辐射能谱的贡献和电子能量损失过程中临界能量的改变都是导致Mrk 421天体的能谱变化的原因.同时，由于式(2)中系数N1和N2中的参数较为复杂，因此在未来的工作中，还需对参数之间的关联性进行更深入的研究.