干涉测量圆柱外表面的误差分析
2020-09-29吴泉英张凌华王全召陈秋白
许 帅,韩 森,吴泉英,张凌华,王全召,陈秋白,王 艳
(1.苏州科技大学,江苏 苏州 215009;2.上海理工大学,上海 200093;3.苏州慧利仪器有限责任公司,江苏 苏州 215123;4.苏州维纳仪器有限责任公司,江苏 苏州 215123)
引言
圆柱形表面高精度元件具有特殊的光学成像特性,广泛应用在航空航天、工业加工以及测量检测等高精密性领域中[1-3]。随着精密轴类零件技术的发展,对轴类元件表面的光洁度、稳定性等指标提出了更高的要求。现在对柱面粗糙度测量方法的种类有很多[4-6],主要可以分为干涉测量法和非干涉测量法两大类。
非干涉测量方法主要有以下几种:1) 接触式测量法。通常是使用触针与被测表面相接触,并在驱动器的带动下在被测区域内按一定轨迹移动。借助传感器获取到接触位置的粗糙度信息,最后整合所有测量的信息,得到整个被测面的粗糙度。但是这种测量方法在测量过程中,探针与待测表面相接触,因而会对待测面的面形造成一定程度的损伤。现在主要的接触式测量仪器有扫描探针轮廓仪和三坐标测量机两种。2)条纹投影法[7-9]。将一个标准条纹投影到待测面的表面,条纹受到面形的调制作用产生了相位变化,对形变相位光栅的相位进行处理分析,就可以得到待检测面的粗糙度信息。3) 样板比对法。样板对比法需要事先准备好一个与待测半径相同的球面或者平面样板,通过直接接触零件来进行比较。这种方法对样板的加工有较高的要求并且适应的检测范围很小,具有一定的局限性,一般只适应于圆柱内表面并且测量精度低,会对待检测样品面形造成一定的损伤。
干涉测量方法主要有:1) 计算机全息法(CGH)[10-14]。将透射过计算全息CGH 而产生的柱面波与待测的柱面进行零位干涉,通过相移算法分析干涉条纹,最终得到待测柱表面的粗糙度信息。计算全息法具有高精度、高灵敏度、可以多次测量等优点,但是需要定制一个特殊的计算全息CGH,制作成本高,并且其自身的误差很难剔除。2) 掠入射零位干涉测量[15-16]。此种方法需要借助使用两个衍射光学元件(DOE)进行测量,两个DOE分别承担着不同的作用。其中一个DOE 用来分离和整形光束,另外一个DOE可以将经反射后变形的波前转换成近似于平面的波前,与理想参考平面光束相互干涉。但是在柱体轴线的方向上,有效波长增加了λ/cosθ,导致在圆柱轴线方向上采样密度的大幅下降,降低了对被测表面粗糙度的敏感性,其中θ为入射角。
针对回转圆柱外表面粗糙度的测量,本文提出了一种干涉测量的方法,在不进行拼接测量[17]的情况下,一次性获取圆柱外表面一整周的形貌信息。此种测量方法需要使用一个特殊的圆台面反射镜,简化了测量步骤,提高了对圆柱外表面的检测效率。
1 测量原理
为了可以一次性获取圆柱外表面的形貌信息,设计使用一个内侧倾角为45°的圆台面反射镜,将圆柱坐标系转换为直角坐标系。当准直光束沿着光轴(z轴)方向入射圆台面反射镜时,圆台面反射镜将会改变光束的传播方向使其垂直入射到圆柱外表面。由于光路可逆,光束将会返回到干涉系统中并与参考光干涉,得到干涉图。圆柱面上的一个母线,对应着圆环状形貌图的一个半径。这样圆柱面就会转变成为一个平面,圆柱外表面的形貌特征可以直接由此平面来体现。该测量方法的核心思想就是将被测柱面分解并在平面内重新构造,通过平面检测的方法,实现了圆柱外表面粗糙度的一次性测量[7]。
图1中PBS为偏振分光镜,PZT为相移驱动器,TF为标准参考镜。当准直光束沿着光轴(Z轴)方向入射,且各光学元件光轴与几何轴心与Z轴重合时,透射标准参考镜的光会按照示意图所示,经倾角为45°的圆台面反射后,垂直入射到待检测圆柱体的外表面。在不存在误差的情况下,入射到圆柱外表面的光将原路返回,经过干涉系统计算后,得到圆柱外表面的形貌信息。测量圆柱的半径为r,高为h。圆台面反射镜底部空心圆盘的外半径为R,内半径为rm,高为rm。光线经过反射镜折转存在一定的压缩,干涉图也会有所变形,对横向分辨率造成一定影响。在实际的测量过程中,实验搭建以及机械加工很难做到如原理图般毫无偏差,在实际检测装置搭建中,必定会存在着一些失调误差,这些误差会对实际测量结果的精度造成一定的影响,为了获得被测圆柱外表面的真实形貌,必须要将这些误差剔除。
2 建立误差数学模型
由于圆柱体具有旋转对称性,所以沿着z轴偏移或者绕着Z轴旋转不会产生失调误差,不会影响实际测量结果的精确性。但若在垂直于Z轴的方向上有一定的偏移,偏移大小为δ,就会给测量结果引入偏移误差;若在搭建检测装置过程中反射镜的轴线没有与Z轴重合,而是有一定夹角α,这就会给测量结果引入旋转失调误差,影响测量的精度。以上两种失调误差分析在圆柱内表面的测量模拟中有讨论过,由于设计的圆台面反射镜有特定的角度需求,且反射的相干光对角度敏感,在加工的过程中不可避免会存在着一定程度的角度误差,所以在误差分析中引入了第3种失调误差即加工角度误差。若加工的圆台面反射镜内侧倾斜角度并不是严格的45°,而是与设计值存在着角度为φ的误差,这样就会给测量结果引入加工角度误差。为了便于计算,以圆柱底部圆心O为坐标圆心,建立圆柱坐标系,圆台面反射镜到参考镜间的距离为S,分别计算表示出这3种失调误差。
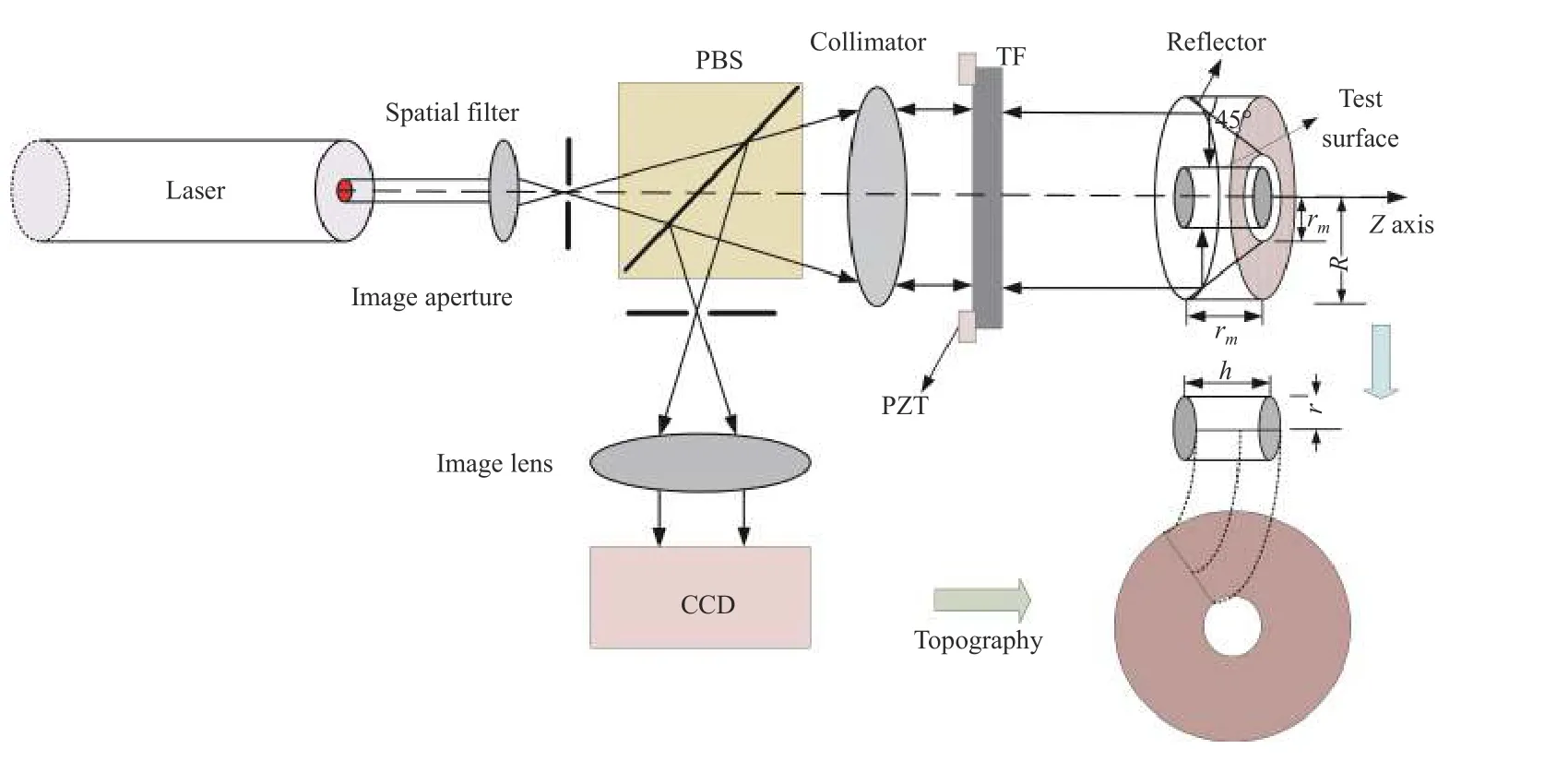
图1 圆柱外表面测量原理图Fig.1 Schematic of cylindrical outer surface measurement
2.1 偏移失调误差
当待测圆柱轴线与Z轴重合,为了方便计算,假设圆台面反射镜的轴线与Z轴平行且在X轴方向有大小为δ的偏移时,圆台面反射镜的其轴线与XOY平面交点由O点位置移动到了O′点,偏移误差光路示意图如图2所示。
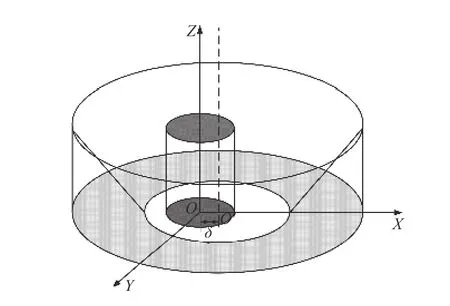
图2 偏移误差示意图Fig.2 Schematic of offset error
图3为径向截面的偏移误差光路图,由于反射镜的轴线与Z轴平行,在准直光的入射下,任意径向截面上光的传播规律都相同,因此通过对单一的径向截面光路的研究,就可以表示出整个圆柱外表面的偏移误差。

图3 偏移失调误差光路Fig.3 Optical path diagram of offset misalignment error
在图3所示的二维坐标系中,设圆柱外表面任意一点P的坐标为(x0,y0),O′点的坐标为(x0−δ,y0)。由于径向截面上的任意一点到干涉仪参考镜的距离都是相等的,所以在计算光程差时,只用考虑在径向截面上的光程差。当不存在偏移误差时,经干涉仪系统发出的准直光束在入射到检测装置后将原路返回,因此径向截面上的光程可以表示为L1=2AP。当存在偏移误差时,如图3所示,入射到圆台面B点的光,经反射后同样到达圆柱外表面P点,经圆柱外表面反射到达圆台面的的C点。此时的总光程可以表示为L2=BP+PC。图3中r1为待测圆柱的径向截面半径,r2为圆柱面反射镜的径向截面半径,反射镜沿X轴方向的偏移距离为δ,圆柱面上任意一点P和坐标原点O的连线PO与X轴的夹角为β。根据图3所示的几何关系可以得到(1)~(6)关系式:
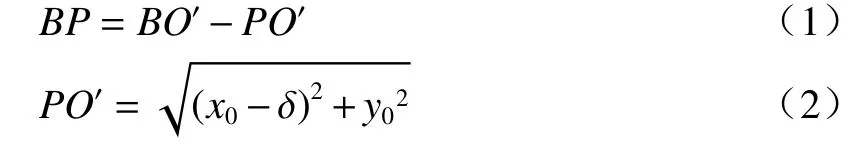
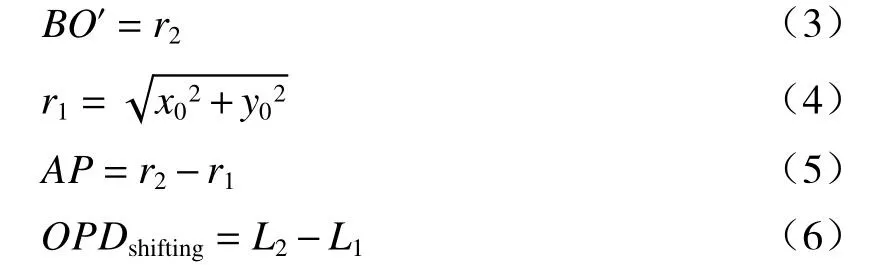
当偏移量δ很小时,BP≈PC,用泰勒公式近似化简(2)式,联立方程组可以解得OPDshifting=为了进一步化简,将直角坐标系转化为极坐标系,有x0=r1cosβ,因此得到OPDshifting=2δcosβ,β∈[0,2π]。
2.2 旋转失调误差
若在检测装调过程时,圆台面反射镜的轴线与Z轴有夹角为α,干涉测量的结果会存在着旋转失调误差。旋转失调误差示意图如图4所示。
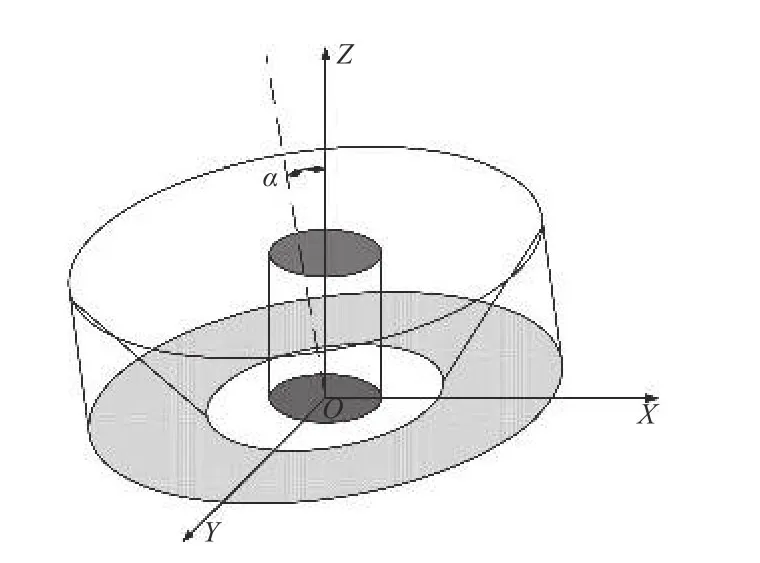
图4 旋转失调误差Fig.4 Schematic of rotation misalignment error
图5是在有失调误差的情况下,光在实际检测中的传播轨迹。当圆台面反射镜轴心与Z轴重合即不存在失调误差时,透射过参考镜TF的光入射到圆台面反射镜内表面Q点,经反射后,垂直入射到待测圆柱外表面的P点,此后光将按照原光路返回。
如图5中的几何光路所示,光程L1=2HQ+2QP。当圆台面反射镜的轴心倾斜且与Z轴的夹角为α时,透射过参考镜的光入射到圆台面反射镜内表面的点B,经圆台面反射镜反射后斜入射到圆柱外表面的P点。由于旋转误差改变了光的理想传播轨迹,所以光并不是垂直入射到圆柱外表面,光束便不能按照原光路返回。此时P点的光经圆柱面反射后到达反射镜内表面的C点,最后入射到参考镜上的D点。因而在存在着旋转误差的情况下,经过圆柱外表面上任意一点P的光程为L2=AB+BP+PC+CD。以圆柱底部圆心O为坐标圆心,建立圆柱坐标系。图5中,M、N、T、P4个点的柱面坐标分别为(0,0,zb),(0,0,zp),(0,0,zc),(r,β,zp)。参考镜到圆柱面反射镜的距离为S,反射镜的底部半径为R,高为rm,待检测圆柱高为h且rm≥h。图5中α′随着P点极角的变化而变化,α′=α·cosβ。经分析可以得到(7)~(15)几何关系式:
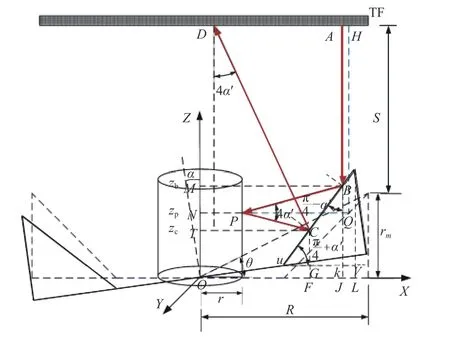
图5 旋转失调误差光路图Fig.5 Optical path diagram of rotation misalignment error
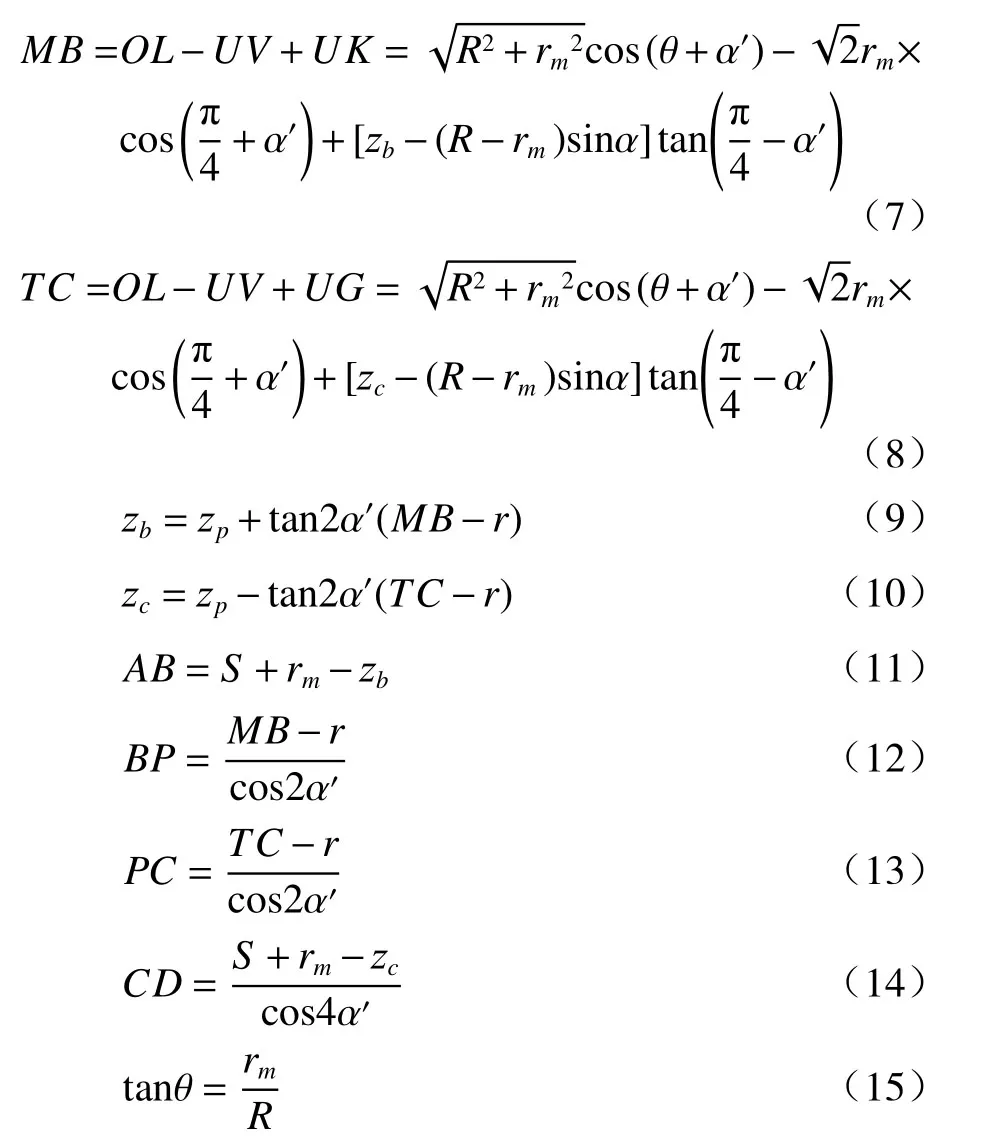
光程差OPDrotation=L2−L1,由于旋转角度α非常小,因此联立上述方程并使用泰勒公式近似求解,得到圆柱外表面任意一点P的旋转光程差:
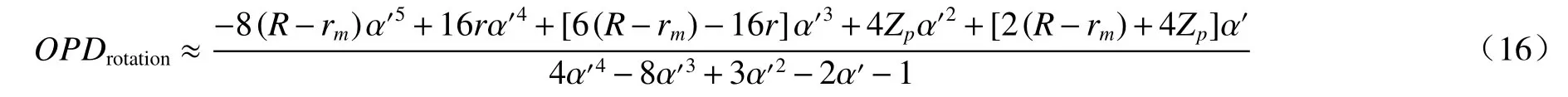
2.3 加工角度误差
检测所用到的圆台面反射镜内侧斜面具有特定的倾斜角度45°,如若实际加工角度与设计角度有大小为φ的误差,那么在测量结果中就会引入加工角度误差,影响测量的精准性。引入加工角度误差的光路图如图6所示。
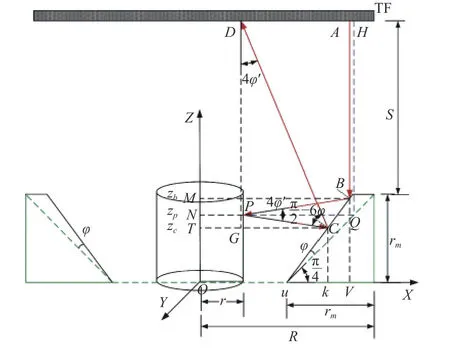
图6 加工角度误差光路图Fig.6 Optical path diagram of processing angle error
当不存在加工角度误差时,透射过测量系统参考镜的光,经过圆柱面反射镜的反射后垂直入射到圆柱外表面的P点,由于满足可逆光路条件,准直光束将原光路返回。具体光路如图6所示,光程L1=2HQ+2QP。当存在加工角度误差且误差角度为φ时,入射到圆柱外表面同一点P的光程为L2=AB+BP+PC+CD。以圆柱底部圆心O为坐标圆心,建立圆柱坐标系。参考镜到圆柱面反射镜的距离为S,反射镜的底部半径为R,高为rm,待检测圆柱高为h且rm≥h。图中φ′随着P点极角的变化而变化,φ′=φ·cosβ。根据上图的几何关系可以得到(17)~(25)等式:
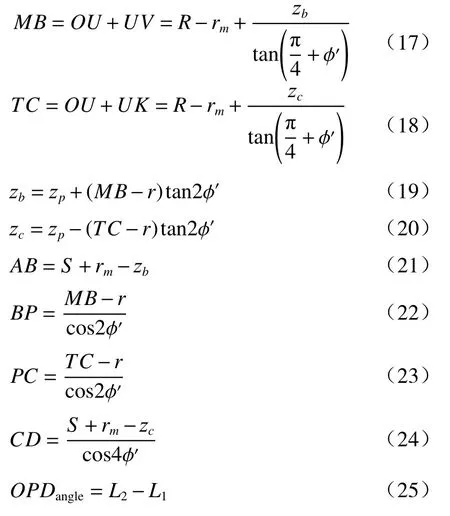
当加工角度误差φ非常小时,使用泰勒公式近似求解可得:
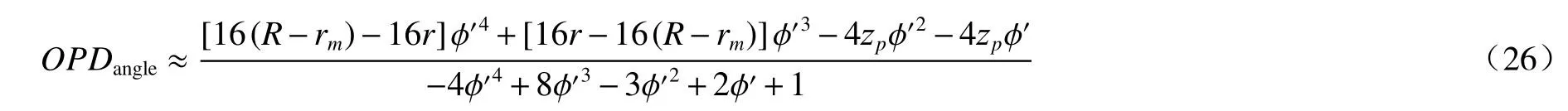
3 误差仿真模拟
3.1 偏移失调误差干涉条纹模拟
当只存在偏移失调误差时,根据偏移量δ的大小,干涉条纹的变化如图7所示。图7为偏移误差量δ分别为0.1 mm、0.3 mm、0.6 mm、0.9 mm时的干涉条纹图,从中可以看出干涉条纹为直条纹且偏移误差量每增加一倍,干涉条纹的数目也增加一倍,偏移量对干涉有着较大的影响。
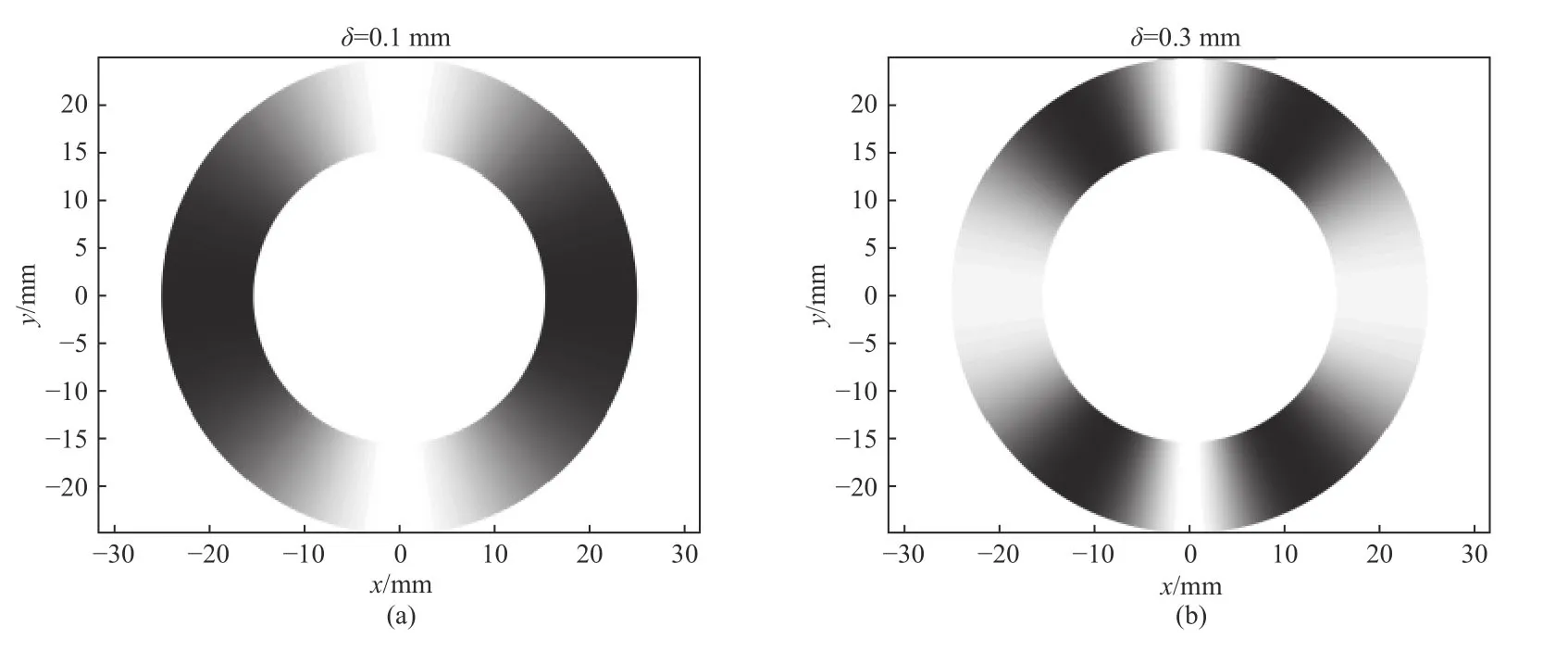
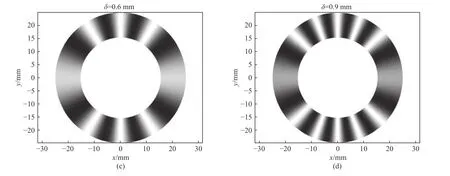
图7 不同偏移误差的干涉条纹图Fig.7 Interference fringe patterns with different offset errors
3.2 旋转失调误差干涉条纹模拟
当只存在旋转失调误差时,随着圆台面反射镜轴线与Z轴夹角α的改变,干涉条纹如图8所示。图8是旋转误差角度α分别为0.001°、0.003°、0.006°和0.009°时的干涉条纹图。从中可以看到,随着旋转误差角度的增大,干涉条纹的弯曲程度与数目有明显的增大,对实际测量的精度有较大程度的影响。
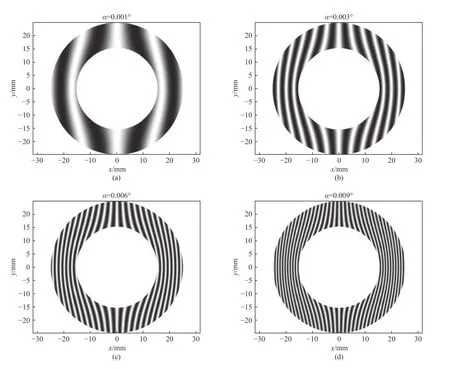
图8 不同旋转误差的干涉条纹图Fig.8 Interference fringe patterns with different rotation errors
3.3 加工角度误差干涉条纹模拟
当只存在反射镜内侧面加工角度误差,且与理想设计角度45°的差值为φ时,随着加工角度误差φ的变化,干涉条纹如图9所示。
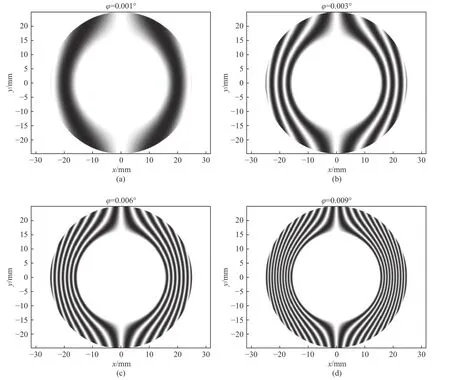
图9 不同加工角度误差的干涉条纹图Fig.9 Interference fringe patterns with different processing angle errors
图9是加工角度误差φ分别为0.001°、0.003°、0.006°和0.009°时的干涉条纹图,很明显可以看出干涉条纹的数量与φ存在着正比的关系。在实际测量过程中,为了保证测量的精度,必须要将这些误差剔除。
4 实验测量
圆柱外表面粗糙度测量实验装置如图10所示,实验装置使用6″口径菲索型干涉仪、两个五维支架(分别固定被测圆柱和圆台面反射镜),干涉仪使用的光源波长为632.8 nm。

图10 实验实测装置图Fig.10 Experimental device diagram
被测圆柱样品的直径为20 mm,高为50 mm。圆台面反射镜的高为30 mm,底部空心圆环的直径为40 mm。图11是将3种失调误差按一定量组合后的干涉条纹图。
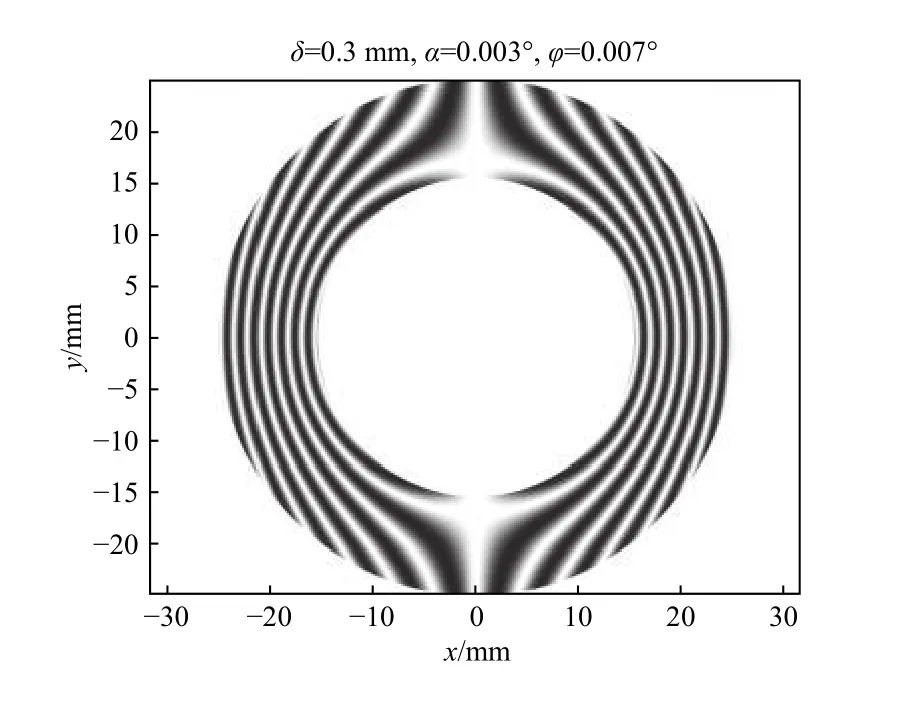
图11 三种误差组合后干涉条纹图Fig.11 Interference fringe pattern after combination of three kinds of errors
实际测量得到的干涉条纹与圆柱外表面的形貌信息如图12所示。
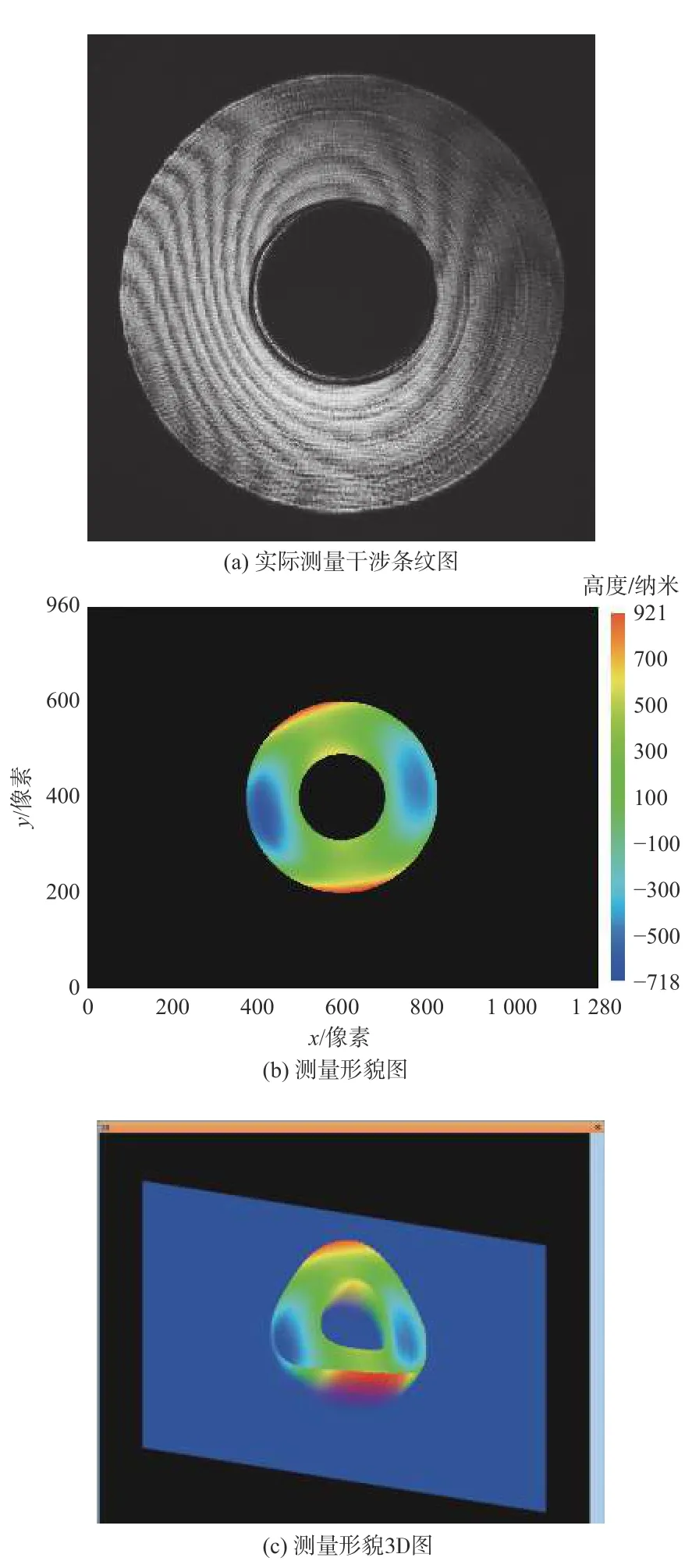
图12 实验测量图Fig.12 Experimental measurement diagram
5 结论
设计了一种可以一次性测量圆柱外表面粗糙度的方法,分析3种失调误差对测量精度的影响,找到光的实际传播规律,在圆柱坐标系下建立数学模型,用数学公式将失调误差对干涉条纹的影响表示出来。根据推导出的几种失调误差公式,使用Matlab 软件模拟出对应误差下的干涉条纹图。将3种失调误差适当地组合在一起,对比实验测量的干涉条纹图,调整实验装置,减少误差量引入。使用模拟结果指导实际测量,提高测量的精确度,准确得到圆柱外表面的形貌信息。
