基于QR码和算术编码的图像加密无损恢复方法
2020-09-29
(四川大学 电子信息学院,四川 成都 610065)
引言
近年来,随着互联网技术和数字通讯技术的快速发展,信息安全问题越来越得到人们的关注。由于具有容量大、加密速度快、可多路并行传输、密匙维度多等固有的优势,光学图像加密技术迅速成为了一个热门的研究方向。这一技术最早可被追溯到1995年,Refregier和Javidi 提出的基于双随机相位编码(double random phase code,DRPE)的图像加密方法[1]。即在4-f系统的空间输入平面和傅里叶变换域平面放置随机相位板,对原加密图像的空间域信息和频域信息分别置乱,得到一个平稳随机分布的白噪声密文图案。随后,由该方法衍生出的其他光学加密方法逐渐被提出,如菲涅尔域DRPE的图像加密方法[2-3]、分数傅里叶域
DRPE的图像加密方法[4-5]、基于光学联合变换器的加密方法[6-7]、基于干涉原理的加密方法[8]等。这些方法丰富和发展了光学图像加密技术,但一些制约其进一步实用化的问题依然存在。例如,由于随机相位板的引入和实验中其他不可控因素,基于光学系统的解密图像往往包含有大量的散斑噪声,这些噪声严重影响了解密后图像的质量。虽然目前提出了许多减弱或者抑制散斑噪声的方法[9-13],但效果都不是很理想。
为了解决这一问题,2013年Barrera 等人首次将QR码(quick response code)作为数据容器引入到光学图像加密系统中[14]。由于QR码具有较强的纠错能力,当部分码字被污染或者发生错误时,依然可以识别出来,使得存储在里面的信息可以无损恢复,因此是一种非常理想的去除光学加密系统中散斑噪声的容器。可由于QR码存储容量有限,存储内容只能为数字、字母,汉字、日文等信息[15],要将一幅灰度图像存入到QR码中,必须要进行数据的转换与压缩。目前主要有两种方法,即将二值图像利用行程编码压缩方法存入QR码[16],以及利用数字之间转换压缩方法将灰度图像存入QR码[17]。由于前者只适合于非常简单的二值图像,而后者只能将一幅32×32像素大小的灰度图像存入到QR码中,因此在实际图像加密的应用中,寻求一种既能有效进行数据压缩,又能处理较大灰度图像的方法仍显得极为重要。
本文提出了一种基于算术编码图像压缩方法,成功地将一幅64×64像素大小的灰度图像存入QR码中进行加密和解密。该方法首先把灰度图像读取为二进制数据,并转换为十进制数,然后利用算术编码的方法压缩十进制数序列得到新的二进制序列,把压缩后的二进制数据再次转换成十进制数据存储到QR码中,最后利用双随机相位编码的方法进行加密和解密。
1 理论基础
1.1 基于算术编码的压缩方法
算术编码[18-20]是一种变字长无损编码方法,将编码数据看作由多个符号组成的序列,直接对该序列进行编码,编码后输出的码字对应于整个符号序列,而每个码字本身确定了0和1之间的一个实数区间。编码原理为:根据信源符号中各个符号所占的概率不同,把[0,1]区间划分为若干个互不重叠的子区间,每个区间的长度为每个信源符号的概率。这样,每个信源符号都可以用其所对应区间内的任何一个实数来表示,在对信源符号进行编码时,便可用相应的区间来表示。例如,要编码的是一个来自4个信源符号{1234}并由5个信源符号组成的符号序列:41312。通过计算得到各信源符号的概率分别为:P(1)=0.4,P(2)=0.2,P(3)=0.2,P(4)=0.2。编码时,首先根据各个信源符号的概率将区间[0,1]分成4个子区间:符号1对应[0,0.4),符号2对应[0.4,0.6),符号3对应[0.6,0.8),符号4对应[0.8,1.0)。符号序列中第1个符号是4,其对应的子区间为[0.8,1.0),因为它是被编码的第1个符号,所以原始信源符号就被缩窄到了区间[0.8,1.0),接下来将这个区间扩展为整个高度,其端点值不变,然后,这个缩窄的区间根据原始信源符号的概率进行细分,并继续对下一个信源符号进行处理。例如,第2个符号是1,1 在初始区间内是占整个区间的前40%,对应的也要占区间[0.8,1.0)的前40%,因此第2个符号的新编码区间变为[0.8,0.88),然后,第3个符号3 占初始区间的60%到80%,则第3个符号的新编码区间为[0.848,0.864),依此类推,第4个符号的新编码区间为[0.848,0.8544),第5个符号的新编码区间为[0.85056,0.85184),这样该区间内的任何一个实数就可以表示整个符号序列。把该十进制区间用二进制表示为[0.11011001101111100101,0.11011010000100100011),忽视小数点,不考虑“0.”,取该区间内码长为最短的码字作为最后实际的编码码字输出,所以对字符串[41312]进行算术编码的输出码字为1101101。
对于一幅灰度图像,对其进行算术编码压缩的具体步骤为:
Ⅰ) 将灰度图利用Matlab 软件读取文件的形式读取为一串二进制序列数据;
Ⅱ) 将Ⅰ)中的二进制数据利用利用文献[17]中的方法转换为相应的十进制数据。具体规则为:步骤1,取4位二进制数;步骤2,如果4位数字是1000 或1001,则将其转换为8 或9,并在4位数字后再次从下一位开始步骤1。如果这4位数字既不是1000 也不是1001,取前3位数字,并将其转换为0到7之间的一个数字。在3位数之后从下一位开始步骤1;
Ⅲ) 把Ⅱ)中的十进制数分为若干小段,对每一小段进行算术编码,将编码得到的二进制字符串组合在一起;
Ⅳ) 将Ⅲ)得到的二进制字符串用Ⅱ)中的方法转换成十进制数,编码完成,整个过程如图1所示。

图1 基于算术编码的数据压缩过程Fig.1 Data compression process based on arithmetic coding
1.2 QR码
QR码是二维码的一种,有40个版本和L、M、Q、H 4个纠错等级,不同的版本和纠错等级存储的数据大小也不同,版本越大,纠错等级越低,存储的数据越多。例如,31版的QR码最多可存储4 417个十进制数字、2677个字母数字组合、1 840个8位字节、1132个中国汉字。各个版本和纠错等级QR码的存储容量如表1所示。
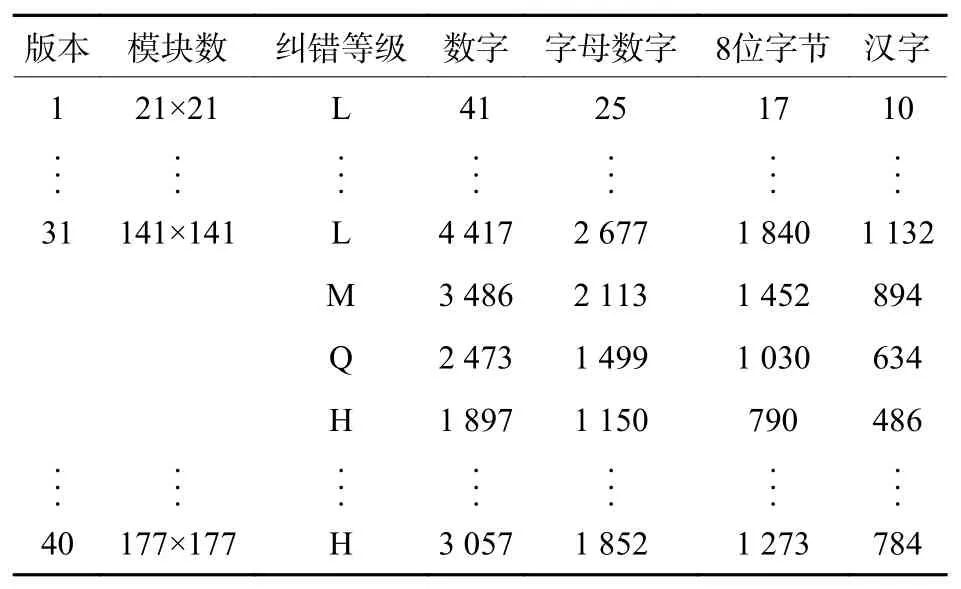
表1 各个版本和纠错等级QR码的存储容量Table1 Storage capacity of QR code with each version and each error correction level
2 实验模拟
为了验证本文所提方法的有效性,利用Matlab软件对实验进行模拟。所选的加密系统为双随机相位编码(DRPE)平行加密系统[1],如图2所示。
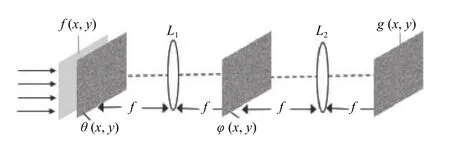
图2 DRPE 加密系统(f(x,y)和g(x,y)为明文图像和密文图像,θ(x,y)和φ(u,v)为随机相位板,L1和L2为傅里叶透镜)Fig.2 DRPE encryption system(f(x,y) and g(x,y) are plaintext images and ciphertext images,θ(x,y) andφ(u,v) are random phase masks,L1and L2are Fourier lenses)
加密和解密过程可以表示为

式中:f(x,y)和g(x,y)分别为明文图像和密文图像;FT和FT−1为傅里叶正、逆变换;θ(x,y)和φ(u,v)是两块随机分布在0到2π 区间的相位板;* 代表共轭。
对于一幅灰度图像,最常见的格式是BMP和JPEG,BMP格式的图像每一个像素值由8位二进制组成,JPEG格式图像是BMP格式的压缩形式,它的数据量要远小于BMP格式的数据量。无论是BMP 还是JPEG格式的图像,都可以以文件形式读取为一串二进制序列数据。以图3(a)灰度值较丰富的Lena 图为例,大小为64×64像素BMP格式的图像二进制文件大小为5.05 kB,可以读取为41376个二进制数字序列,在本文中我们采用的是压缩后的JPEG 文件(见表3),二进制文件大小为3.06 kB,读取为二进制数字序列为25088个,用文献[17]的方法转化的十进制数为8043个,使用算术编码后的二进制数字为19266个,最后再次转化为十进制数字有4395个,将这些十进制数存入31版纠错等级为L的QR码中,结果如图3(b)。然后利用DRPE 光学系统对3(b)进行加密和解密,加密后的密文图像的实部和解密后的QR码图像如图3(c)和3(d)。31版纠错等级为L的QR码[15],错误纠正码字数480个,最少可纠正240个错误码字,解密后的QR码所包含的噪声导致的错误码字数远小于240,所以解密后的QR码可被轻松识别,图3(e)为最后恢复的原始图像。

图3 实验模拟结果Fig.3 Experimental simulation results
为了更好地说明本文所提方法的特点,对表示图像数据量的十进制数字压缩效率采用以下公式:

式中:P代表压缩效率;M代表压缩后的十进制数字个数;N代表原始图像所有灰度值十进制数字个数的总和。以图3(a)中的Lena 图为例,分别计算文献[16]中行程编码的压缩方法、文献[17]中的压缩方法和本文所提出方法的压缩率,结果如表2所示。

表2 不同方法的压缩率Table2 Compression ratios of different methods
由表2可以看出,本文所提出的压缩方法的压缩率要优于文献[16]和文献[17]中的方法,如果要将一幅大图像存入QR码中,本文提出的方法效果更佳。
3 讨论
对于一幅灰度层次较饱满的图像,例如Lena图,采用本文所提出的压缩方法,最多可以将一幅64×64像素大小的图像存入到QR码中,对于一张128×128像素或者256×256像素大小的灰度图像,则要采用多张QR码。表3为不同灰度图的压缩信息,对灰度层次较少的图像,由于图像冗余度大,压缩率高,采用本文的方法可以将一幅128×128像素的JPEG图像压缩后存入到QR码中,通过光学加密系统可以得到无损解密的图像。而对于一张灰度值只有0和255的二值图像,则可以将256×256像素或者更大的JPEG图像存入QR码,如图4所示,为了视觉效果更好,我们对128×128像素的图像做了放大处理。此外,由于QR码有4个纠错等级,不同的纠错等级数据容量不同,在实际的光学加密系统中,往往会引入其他噪声,所以在可选择的纠错等级和版本中,我们一般选择版本低和纠错等级高的QR码进行加密和解密。
本文所提出的基于算术编码的压缩方法,理论上可以多次使用,重复压缩,但由于每次压缩都需要记录每个灰度值的概率,以便在解压时使用,在实际的图像加密应用中,这就会增加密钥数据的传输量,并不利于加密技术的实际应用。

表3 不同灰度图的压缩信息Table3 Compression information for different grayscale images

图4 不同类型图像加密结果对比Fig.4 Comparison of encryption results for different types of images
4 结论
QR码作为数据容器在光学图像加密中起着非常重要的作用,但由于实际图像通常数据量较大,超出了QR码的存储容量,因此目前只是将一些简短的表达或者32×32像素的灰度图像存储到QR码中,远不能满足实际加密的需求。本文提出了一种基于算术编码的图像压缩方法,将灰度图像首先读取为二进制数据并转换为十进制数,再将十进制数利用算术编码的方法压缩为二进制数,最后再转换成十进制数,使得原始图像的压缩率极大提高,成功地将一幅64×64像素的灰度图像压缩到QR码中,并利用DRPE系统加密和解密,得到无损恢复的解密图像。此方法在未来有望用于视频及其他多媒体信号的加密。
