基于GA-PLS 算法的河网水体化学需氧量高光谱反演

蔡建楠，刘海龙，姜 波，何甜辉，陈文杰，冯志伟，黎倬琳，邢前国*

（1.中山市环境监测站，广东 中山 528403；2.中山市生态环境局，广东 中山 528403； 3.中国科学院 烟台海岸带研究所/中国科学院海岸带环境过程与生态修复重点实验室，山东 烟台 264003）

0 引 言

【研究意义】水质监测是河流水污染防治工作的重要组成部分。传统的水质监测方法存在成本高昂、采样及分析过程需时长、时空代表性差等缺点，难以满足当前形势下水环境管理的需要[1-2]。近年来，高光谱水质遥感以其检测速度快、无二次污染、精确度高、可与航空技术结合、可实现大面积覆盖等优点，在水质参数定量化监测中具有较大的应用潜力[3-4]。高光谱水质监测主要基于水体实测光谱丰富的谱域信息，通过建立光谱特征和水质指标的关系模型，实现对水质指标的反演[3]；但高光谱数据也存在数据冗余、易受环境噪声影响、不同波段间数据存在共线性等问题，影响水质反演精度及稳定性[5-6]。采取合适的数学建模方法进行数据优化和波段筛选，实现冗余变量的剔除和模型的优化，是水质反演模型建立的关键环节[7-8]。

【研究进展】高光谱环境遥感数据的波段筛选方法主要有遗传算法（GA）、无信息变量消除法（UVE）、竞争性自适应重加权算法（CARS）、连续投影算法（SPA）等[9]。其中GA 是一种模拟自然进化搜索最优解方法，GA 与偏最小二乘法（Partial Least Squares, PLS）结合而成的GA-PLS 算法，综合了GA 全局优化搜索能力和PLS 可有效解决变量间多重共线性问题的能力，成为光谱反演模型建立的研究热点，被广泛应用于化工、食品、农业等领域[8,10-12]。

【切入点】在水质遥感监测领域，GA-PLS 主要应用于湖泊水库中透明度、叶绿素a、悬浮物和浊度等光学活性参数的反演研究[13-14]，而针对河网水体水质综合指标的高光谱反演研究报道较少。本研究以广东省中山市有代表性的河流、水渠为监测对象，以化学需氧量（COD）为水质综合评价指标，通过现场同步监测获得水体高光谱数据和COD 质量浓度，建立河网水体化学需氧量（COD）质量浓度高光谱反演模型。

【拟解决的关键问题】通过本研究验证GA-PLS算法对高光谱水质反演模型预测效果的改善作用，从而为河网水体水质高光谱监测提供参考。

1 材料与方法

1.1 研究区概况

中山市地处粤港澳大湾区几何中心，珠江口西岸，北连广州，毗邻港澳；属珠三角感潮河网区，辖区内河流密布，除主要外江河道外，有各种规模的内河涌、排灌渠等超过1 000 条。中山市经济发达，产业集群密集，近年来随着城市快速发展和人口不断增加，河网水体多数受到一定程度的污染，水质复杂多变。

1.2 光谱测量及水质监测

光谱测量和水质监测于2019 年7—9 月实施，监测对象尽可能覆盖中山市不同规模的河流和渠道。剔除个别离群值后，共获得146 个点位的现场实测光谱数据和水质样品。使用的光谱测量设备为美国Ocean Optics 公司USB4000 光谱仪，光谱分辨率<0.2 nm。测量时选择晴天无云或少云天气状况下，距12:00 约3 h 的时段内进行，以最大限度地降低太阳耀光影响。在每个点位离河流水面0.5 m 处，测量河流水体上行辐射亮度（Lu）、天空辐射亮度（Ls）和太阳下行辐照度（Ed）。测量前使用标准白板进行仪器定标，后进行3 次测量后取平均值作为光谱测定结果。计算测点光谱反射率Rrs计算式为[15]：

去除高光谱数据中噪声较大、信噪比低的两端波段，最终每个测点保留400～900 nm 光谱范围共2 534个波长的反射率数据。

监测点的水样采集与光谱测量同步进行，采集河流表层0～20 cm 处混合样，加入固定剂保存并送至实验室分析，监测项目为反映河流水质的综合性指标COD，分析方法依据《水质化学需氧量的测定重铬酸钾法》（HJ 828—2017）。

1.3 基于GA-PLS 的波段优选

1.3.1 GA-PLS 算法原理及实现

GA 是一种非导数的随机优化方法，借鉴生物界自然选择和进化机制，利用选择、交换和突变等算子的操作，随着不断的遗传迭代，使目标函数值较优的变量被保留，较差的变量被淘汰，最终达到最优结果[8,11]。PLS 是一种基于高维投影思想的非参数回归方法，综合了多元线性回归分析、典型相关分析和主成分分析的基本功能，特别是当各自变量集合内部存在较高程度相关性时，通过提取主成分能对系统中的数据信息进行分解和筛选，提取对因变量解释性最强的综合变量，辨识系统中的信息和噪声，有助于建立最优模型[16-17]。将GA 和PLS 结合可融合2 种算法的优势，建立更加稳定、简便、预测能力更强的模型。GA-PLS 算法的基本思想是将PLS 算法对因变量预测效果的评价指标作为GA 的适应度函数，用GA 进行波段筛选，再用偏最小二乘法方法对筛选后的自变量建立反演模型。GA-PLS 算法实现流程见图1。

图1 GA-PLS 算法实现流程图 Fig.1 GA-PLS algorithm implementation flowchart

1.3.2 GA-PLS 算法参数设定及结果处理

GA 算法采用 PLS 交叉校验均方根误差（RMSECV）作为适应度函数，控制参数设定为：群体规模为30，最大迭代次数为100，交叉概率为50%，变异概率为1%，以遗传迭代次数为收敛终止条件。PLS 算法采用舍一交叉验证方法（PRESS）确定主成分的选取个数。由于GA 算法单次计算结果具有随机性，为确保得到稳定的筛选结果，对数据执行10 次GA-PLS 重复运算并累积记录每次运算得到的入选波段和入选频率。

1.4 模型的建立与评价

将146 个样本按照COD 质量浓度升序排列，按照1∶4 的间隔依序选择验证数据和建模数据，可将数据划分为建模集（116 个样本）和验证集（30 个样本）。其中建模集用于GA-PLS 运算以筛选特征波段并建立PLS 回归模型；验证集用于验证筛选得到的特征波段及回归模型对水体COD 质量浓度的反演效果。同时将全谱段范围的反射率数据建立PLS 回归模型，以比较GA-PLS 算法和常规PLS 算法的效果差异。模型建立和验证效果分别采用模型决定系数R2、建模集方根误差RMSEC 和验证集方根误差RMSEP 进行评价。各评价指标计算式为：

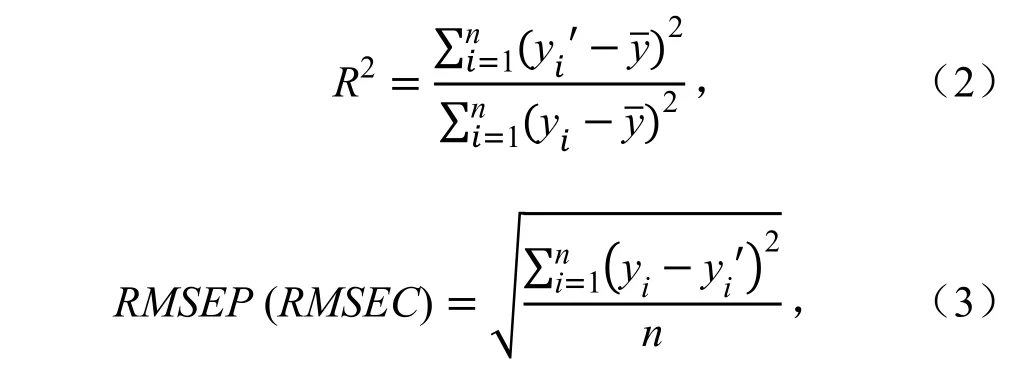
式中：yi为建模集（验证集）第i 个样本COD 质量浓度实测值；yi′为建模集（验证集）第i 个样本COD质量浓度反演值为建模集COD 质量浓度实测值平均值；n 为样本数。

2 结果与分析

2.1 光谱反射率与COD 质量浓度的关系

根据水质监测结果，146 个水质样品测得的COD质量浓度范围为5～32 mg/L，平均值为13.7 mg/L，标准差为6.3 mg/L，偏度和峰度分别为0.799 和-0.004。按照《地表水环境质量标准》（GB 3838—2002）Ⅱ～Ⅲ类水的限值作为区间划分标准，将各测点的高光谱反射率数据分别按照不同的COD 质量浓度分类，以分析不同COD 质量浓度水平下水体高光谱特征差异，（图2）。

在400～700 nm 波段范围内水体光谱反射率对低COD 质量浓度水体有较好的区分度，Ⅱ类水质水体光谱反射率在此波段范围内均显著高于其他水质类别的水体；而在波长大于720 nm 的波段范围内，则出现Ⅳ类水质水体的光谱分辨率高于Ⅲ类水质水体的现象。表明水体光谱反射率与COD 质量浓度存在一定的相关性，但在不同波段范围内相关关系特征规律不同；总体上表明基于光谱分辨率的水体COD 质量浓度反演具有较好的可行性。

图2 不同COD 质量浓度水平对应的水体高光谱反射率 Fig.2 Hyperspectral reflectance of water body with different COD concentration levels

2.2 波段筛选过程及结果

样本集数据经过10 次GA-PLS 重复运算，得到的入选波段及累积入选频率见图3。图3 显示在610～660、680～730、840～870 nm 等波段范围内均有连续的波段入选；入选频率最高为650、720、763、818、842、873 nm 附近波长的波段，上述波段入选频率均超过 20%；入选频率较低的波段范围为400～430、530～560、780～800 nm，表明该上述波段范围内的水体光谱反射率可能与COD 质量浓度相关性较低。

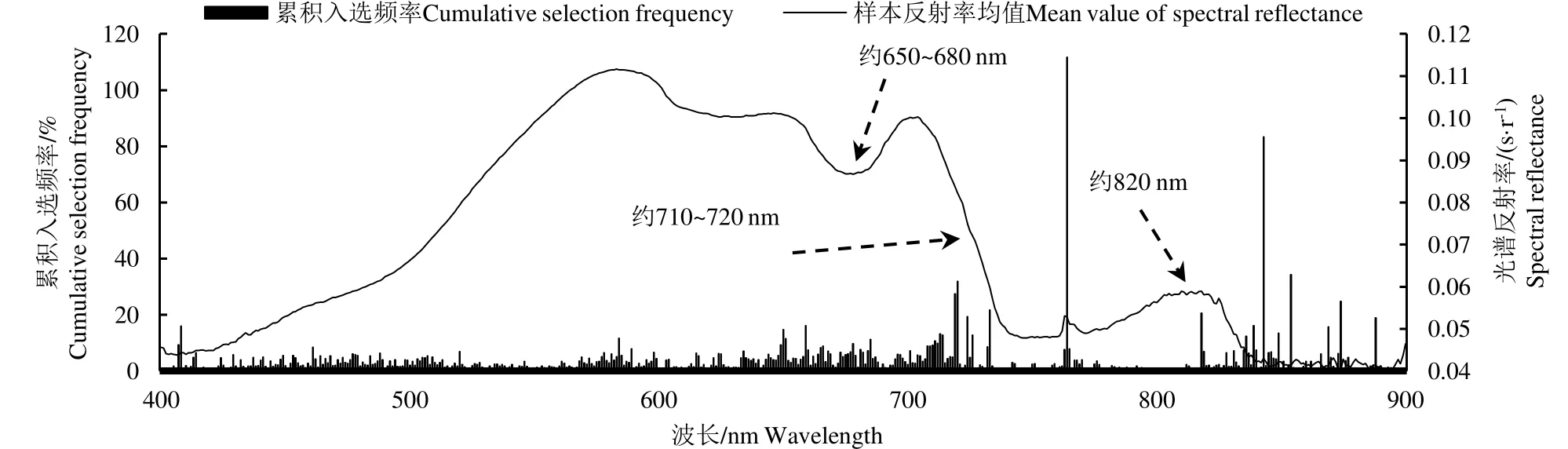
图3 GA-PLS运算得出的入选波段及频率 Fig.3 Selected bands and frequencies from GA-PLS calculation

2.3 水质反演模型预测效果及评价

为探索不同入选波段数量对模型建立及验证效果的差异，分别选取累积入选频率大于15%（共74个波段）、大于10%（共140 个波段）、大于5%（共471 个波段）和大于2%（共1 235 个波段）的波段作为输入变量进行PLS 算法建模，并和基于全谱段PLS模型的预测效果相比较，评价结果见表1。由表1 可知，与全谱段PLS 模型相比，经过GA-PLS 算法筛选后得到的不同波段组合作为PLS 模型的输入变量，模型稳定性基本保持不变或有所提高。在各种波段组合中，以471 个波段作为输入变量可得到最佳的验证效果，验证集RMSEP 为4.887 mg/L，较全谱段PLS模型降低11.4%；而以74 个波段（占全波段数的2.9%）作为输入变量时，模型仍然保持良好的稳定性和验证精度，模型建立和验证效果评价指标均优于全谱段PLS 模型，实现了对输入参数的有效缩减。

水质类别判定是水环境管理和评价的重要工作，故本研究按照《地表水环境质量标准》（GB3838—2002）所划分的水质类别，将全部146 个样的模型反演值予以分类，并与实测值对应水质类别进行比较，结果（图4）显示，模型对全部水质样品的水体类别分类准确率为72.0%，其中对Ⅱ、Ⅲ类水质水体分类准确性可达83.9%，但对Ⅳ、Ⅴ类水质水体的分类准确性较差，为21.4%。从全体样本COD 实测值与模型反演值对比结果看（图5），该模型对COD 质量浓度小于20 mg/L 的水体样本有较好的反演精度，但对于较高COD 质量浓度样本的反演结果偏低。由于本研究中样本COD 质量浓度主要处于Ⅱ～Ⅲ类水质范围内，说明在样本COD 质量浓度主要分布范围内，基于GA-PLS 的高光谱水质反演模型具有较高的验证精度。

表1 模型建立和预测效果评价 Table 1 Evaluation of model establishment and prediction effect

图4 GA-PLS 模型水质分类结果与实测分类结果比较Fig.4 Comparison of water quality clasification results by GA-PLS model with measured value

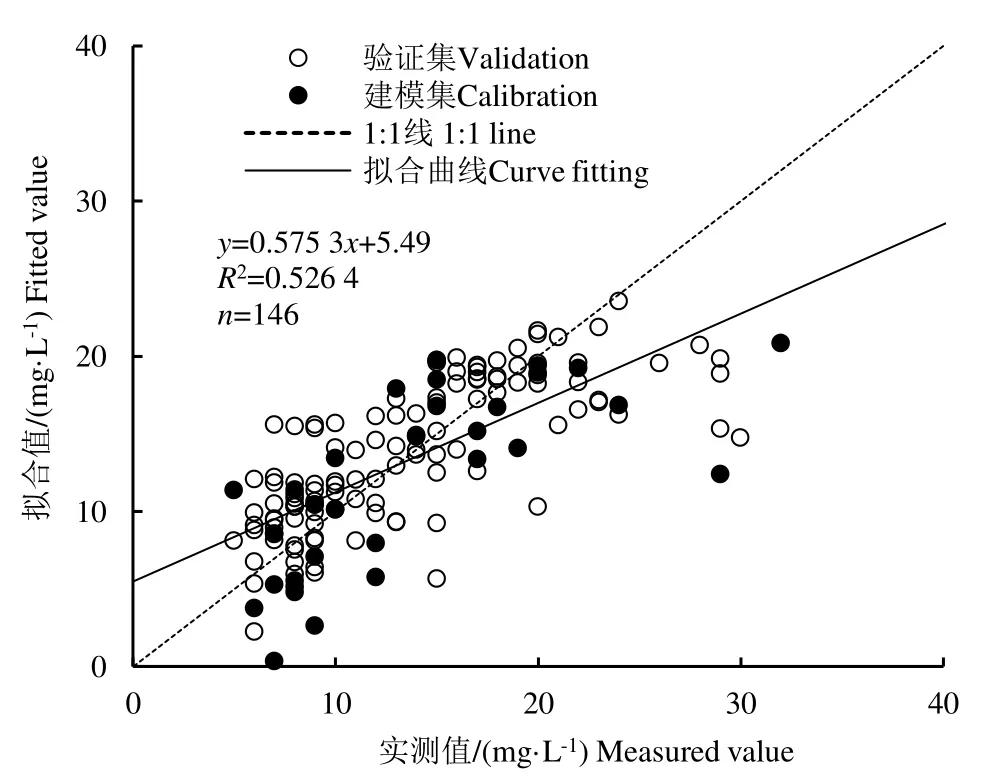
图5 GA-PLS 模型反演值与实测值比较 Fig.5 Comparison of GA-PLS model retrieval and measured values

3 讨 论

本研究采用GA-PLS 算法对高光谱数据进行波段筛选，实现了高光谱数据的降维，当采用数量仅为全谱段3.4%的优选波段作为自变量进行PLS建模时，模型建立及验证效果仍然优于全谱段PLS 建模，说明GA-PLS 算法可有效去除与水体COD 质量浓度相关性小的波段数据，从而提高水体COD 质量浓度高光谱反演模型的稳定性和预测能力。

对GA-PLS 算法筛选得到的部分特征波段（图3中箭头标示处）做进一步分析可见，筛选得到的部分特征波段与水中藻类、悬浮颗粒物的光谱吸收、反射特征波段一致：如650～680 nm 波长范围内的反射低谷由藻类吸收所致[18]；710～720 nm 波长范围内反射率下降与水分子吸收过程密切相关，反映水体洁净程度；约820 nm 波长处的反射峰则是水体悬浮颗粒物散射程度加强而形成[19]。上述结果表明受测水体中悬浮颗粒物、藻类对COD 质量浓度影响较大，是水体COD 的主要来源；也反映GA-PLS 算法选取的特征波段具有较好的合理性和指示意义。此种特性使得GA-PLS 算法在水质高光谱监测中具有广阔的应用前景，可为同类型水体光谱监测的波段选择或多光谱传感器的波段设计提供重要参考，也有助于深入开展水体COD 光谱吸收特征及机理研究。

由于GA-PLS 算法结果具有随机性，多次运算后可能得到不同的波段筛选结果，选择何种方法确定最终输入变量对模型效果有一定的影响。本研究以各波段累积入选频率为标准筛选特征波段，可综合多次运算的结果，方法简便易行。但最优变量组合的确定仍然有必要结合目标污染物的光谱吸收特征、不同波段间反射率的相关性和预测精度的要求等，开展进一步研究。

4 结 论

1）基于GA-PLS 算法的河网水体COD 质量浓度高光谱反演模型效果优于全谱段PLS 模型。采用不同数量的筛选波段作为输入变量，验证集RMSEP 最小为4.887 mg/L，较全谱段PLS 模型降低11.4%；以筛选后的74 个波段（占全波段数的2.9%）作为输入变量时，模型仍可保持良好的稳定性和反演精度，表明GA-PLS 算法可以实现对模型输入参数的有效缩减。

2）模型对全部水质样品的水体类别分类准确率为72.0%，对Ⅱ、Ⅲ类水质水体分类准确性达83.9%，表明在样本COD 质量浓度主要分布范围内，GA-PLS算法模型有良好水质类别分类准确性。

3）通过GA-PLS 算法可对高光谱数据进行特征波段筛选，实现数据的降维优化，并进一步简化模型；GA-PLS 算法筛选得出的部分特征波段具有较好的合理性，有助于揭示COD 的主要来源构成，可为水质高光谱监测传感器设计和水质反演机理研究提供参考，在河流COD 快速监测中具有广阔的应用前景。