高效二元叶轮模型级参数化优化研究

（重庆通用工业（集团）有限责任公司）

0 引言

大型化工用压缩机为多缸多级结构，采用二元叶轮有利于控制成本和尺寸重量，降低转子设计难度[1-3]。但传统二元叶轮效率普遍低于高效三元叶轮，多级累积会导致整体效率不足，因此，有必要针对二元叶轮开展模型级优化设计以提高机组运行效率，缩短人工设计周期。

模型级是大型压缩机研发关键技术之一，沈鼓集团联合其他高校在这方面开展了大量工作。如许敏等[4]开展了离心压缩机模型级叶轮外径切削研究，在验证CFD结果的同时对比了切削前后级性能关系。谭佳健等[5]开展了过程工业用离心压缩机模型级轴向推力测量研究，得到了叶轮盘侧和盖侧间隙经验分布规律，以及轴向推力的组成和变化规律。卢傅安等[6]通过优化设计、CFD分析与实验测试完成了某长输管线离心压缩机模型级的开发。冀春俊等[7]研究通过抑制某高马赫数离心压缩机模型级叶轮内部流动分离问题有效提高了设计工况效率和变流量工况运行范围。刘艳[8]、Guillaume[9]和Liyan[10]等开展了压缩机相似准则和相似变化研究，以进行缩放设计与性能预测。谭佳健等[11]还具体研究了网格数量、湍流模型和盖盘侧间隙等因素对数值模拟精度的影响。

现代优化理论的发展以及算法的不断改进提出了新的设计方法，即建立以经典一维设计理论为基础，结合参数化造型方法的设计方法，引入以高效全局优化算法为核心，辅之以全自动网格划分、求解和后处理的CFD分析技术的自动优化系统，来进行高效二元叶轮模型级的开发，能够有效简化模型级设计难度[12-13]，并保障模型级设计的可靠性。曹国安[14]、吴亚东[15]等分别研究了基于改进Kriging代理模型的自适应序列优化算法和Pareto多目标算法，并建立了优化平台系统针对离心压缩接蜗壳进行了有效的优化分析。唐新姿[16]等采用拉丁超立方试验设计、Kriging模型和NSGA-Ⅱ算法进行了离心压气机叶轮变流量工况多目标优化，不仅有效提高了设计流量效率和压比，也拓宽了稳定工作范围。此外，尹熙文[17]等使用CFD技术与人工神经网络以及遗传优化算法相结合的方法，对离心式压缩机基本级DARV回流器叶片型线进行了优化设计可以提高整级效率。

本文以大型化工用压缩机中二元叶轮模型级为研究对象，结构包括叶轮、无叶扩压器、弯道、回流器叶片以及下一级弯头，建立了针对整级的通用参数化设计方法，开展了全局优化设计，最终获得性能优秀且满足约束条件的二元叶轮模型级。此外针对现有产品某型二元叶轮级开展了自动优化研究，在提高设计效率的同时拓宽了小流量工况稳定运行范围，证明了所开发的参数化优化设计方法的有效性，为大型压缩机二元叶轮模型级设计提供了技术参考。

1 参数化设计方法

稳健、通用的模型级参数化设计方法是对模型级进行气动设计和全局优化的基础。本文通过一维设计获得模型级的主要结构参数，并结合所建立的参数化设计方法完成了二元叶轮模型级的结构设计。

本文研究的二元叶轮结构主要包括4个部分：叶轮、扩压器、弯道和回流器。图1为模型级子午流道及叶轮和回流器叶片模型。

图1 模型级子午面结构Fig.1 Meridional structure of model stage

图2为叶轮和回流器叶片的参数化设计方法，利用典型几何参数（包括进出口几何角等）对叶片中弧线进行造型，再通过控制点对中弧线和叶片的厚度进行设计。

2 优化设计方法

2.1 优化流程

研究采用的优化设计方法耦合了CFD求解技术、二元叶轮模型级参数化方法和高效全局优化算法，图3给出了该优化平台的设计流程，共包括4个模块，优化算法模块、变量解析模块、性能分析模块和约束处理模块。其中，优化算法模块控制设计优化的进程，变量解析模块负责完成参数化。

图3 优化设计流程Fig.3 Flow chart of optimization design

2.2 优化算法

优化算法控制整个优化的进程，是模型级优化设计的核心，决定了性能优化效率和结果可靠性。针对模型级优化多变量、设计空间复杂的特点，本文采用基于多点搜索的MSEGO算法。

MSEGO算法基于EGO算法，采用多点搜索加密采样点进行迭代寻优，可以更好地兼顾全局最优性和局部最优性，其算法流程如图4。该算法采样点加密准则为选择Kriging模型所建立的响应面最优值的位置，预测方差最大位置，GEI函数值最大的位置，获得新采样点，并依据采样点距离进行筛选，每次加入新采样点3～5个，重建响应面迭代寻优。该方法可以提高优化算法的全局收敛性，避免了单点迭代失败导致优化终止的问题，能够更好地达到优化效果。

图4MSEGO算法流程Fig.4 Flow chart of MSEGO algorithm

为验证MSEGO算法的有效性，利用典型的多峰值非线性Dixon-Szego系列函数对EGO算法和MSEGO算法进行性能测试，对比了采用二者得到的全局最优解与理论全局最优解的差距，如表1所示。对比相对误差，MSEGO算法求得的最优值相对理论最优值的误差均小于EGO算法，进一步表明，MSEGO算法相对EGO算法全局搜索能力显著增强。

表1 函数测试结果Tab.1 Function test results

为对比MSEGO算法和EGO算法的优化效率，表2给出了优化过程二者所需的函数评估次数和优化迭代次数。在初始样本数一样的条件下，MSEGO算法的函数评估次数相对较多，但迭代次数减少。

表2 函数评估和优化迭代次数Tab.2 Number of function evaluation and optimization iteration

综合来讲，MSEGO算法虽然函数评估次数增多，但迭代次数减少，在并行条件下其优化效率与EGO算法相差不大，但其优化结果准确性远高于EGO算法，从而有效保障了模型级优化设计效率和可靠性。

3 高效二元叶轮模型级优化设计

3.1 数值方法和模型

以某型离心鼓风机为例进行了数值方法精度验证，如图5所示，其中蓝色曲线为在一般CFD计算（绿色曲线）基础上针对运行状态进行模型变形修正后得到的性能曲线，可见其与机组测试数据（红色曲线）吻合度良好，在曲线最小流量、设计流量和最大流量工况，二者压力偏差分别为1.24%、0.63%和2.28%，效率偏差分别为2.1%、0.25%和1.14%。

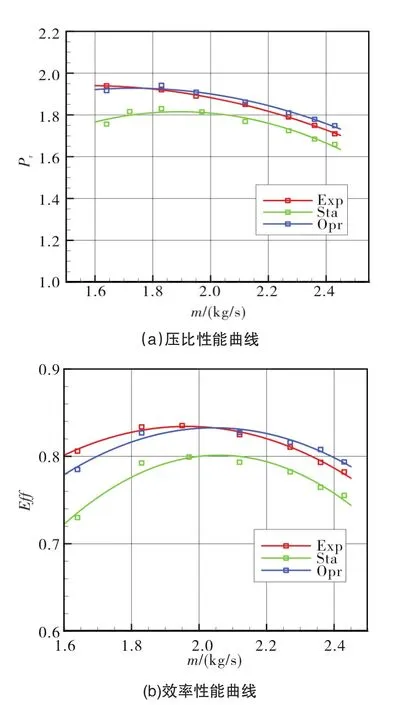
图5 数值计算与测试结果对比Fig.5 Comparison of numerical calculation and experiment results

图6给出了本文所采用的模型级计算网格。计算过程中设置进口轴向进气，固壁面设为绝热边界，采用光滑无滑移边界条件，密封进出口交界面全部设为内部连接面以减少数据传递误差。通过对网格进行无关性验证，最终选择网格约450万。数值计算中，考虑结构的周期性，取单通道的模型作为研究对象，两侧采用周期性边界。

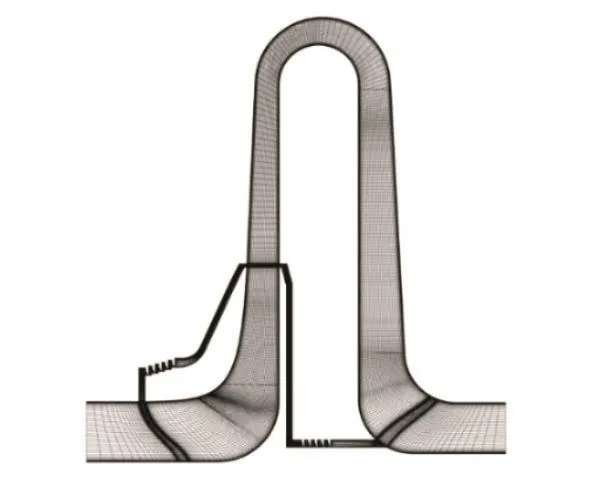
图6 模型级子午面网格Fig.6 Meridional mesh of model stage

3.2 模型级性能分析

本文针对氮气工质压缩机，在初始设计结构基础上，利用建立的优化系统，以总压比、转速、外径为约束条件，以提高效率为目标，经过多轮优化，最终得到高效且稳定运行范围宽广的二元叶轮模型级。

以设计工况下的流量作为标准，其他流量参照设计流量无量纲化，得到图7所示的模型级性能曲线。在设计流量下，模型级效率在83%以上，压比满足设计要求。在80%～110%流量范围内模型级的效率均高于81%，90%流量时模型级的效率最高；在60%～120%流量范围内模型级的效率均高于75%。整体性能达到行业先进水平，且压力性能曲线表明在整个流量范围内模型级均可稳定运行。

图7 模型级性能曲线Fig.7 Performance curves of model stage

3.3 变工况流场分析

对不同流量工况下模型级的内部流场进行分析，可以评估该模型级的设计优劣及其原因，这也是进行后续优化的基础。为此，针对上述模型级性能曲线，进一步从流场结构和气动参数分布进行讨论。

图8为设计工况下模型级子午流道流线和熵分布。可见除叶片进口轮盘侧圆弧过渡处（该处结构考虑加工要求）存在小范围的流动分离以外其他结构处流动情况比较合理。图9给出了设计流量下，模型级50%叶高截面的相对速度和流线分布。可知叶轮内部主流区域内流动状况良好。受回流器叶片出口安装角的影响，回流器内部在中后段存在小范围的低速区，可以在考虑对下级叶轮进口影响的前提下进行适当优化。

图8 设计工况子午面流线和相对速度分布Fig.8 Streamline and relative velocity distribution in meridian plane at design condition

图9 设计工况50%叶高截面相对速度分布Fig.9 Relative velocity distribution in mid-span section at design condition

图10和图11分别给出了60%流量工况下，模型级子午流道和50%叶高截面的相对速度和流线分布。在小流量工况下，扩压器轮盖侧气流受逆压梯度的影响，产生了一定范围的流动分离，并且叶轮主流区域的中后部出现了明显流动分离和低能流体堆积现象，而回流器叶片吸力面侧也出现了大范围的流动分离，造成模型级的效率明显下降。结合图7（b）压力性能曲线说明流场结构的恶化导致叶轮做功能力即将开始下降，若流量进一步减小会导致模型级进入失速工况。

图10 60%流量工况子午流道流线和相对速度分布Fig.10 Streamline and relative velocity distribution in meridian plane at 60% flow rate condition

图11 60%流量工况50%叶高截面相对速度分布Fig.11 Relative velocity distribution in mid-span section at 60% flow rate condition

图12和图13给出了120%流量工况下，模型级子午流道以及50%叶高截面的相对速度和流线分布。在大流量工况下，模型级内部不存在明显的流动分离现象，且叶轮中喉部区域气流加速明显，摩擦损失和粘性损失增加，因此120%流量工况模型级的效率相对较高但低于设计工况。

图12 120%流量工况子午流道流线和相对速度分布Fig.12 Streamline and relative velocity distribution in meridian plane at 120% flow rate condition

图13 120%流量工况50%叶高截面相对速度分布Fig.13 Relative velocity distribution in mid-span section at 120% flow rate condition

通过上述性能曲线分析和模型级内部流场细节说明本文设计的二元叶轮模型级整体性能良好，也证明了本文采用的模型级参数化优化设计方法是有效的。

4 典型二元叶轮级优化

为了进一步验证该优化系统的可靠性，针对现有产品某二元叶轮级进行了优化研究。选择设计工况效率最大为优化目标，对总压比和堵塞流量进行约束，采用健壮性较好的进化算法进行全局寻优。

如图14所示，优化设计(Opt design)显著拓宽了小流量工况范围，失速流量由原叶型(Ref design)的90%设计流量减小至70%。此外，在整个运行工况范围效率均有明显提高，其中在设计工况效率提高了1.84%，而在近堵塞工况效率提高了6.83%。压比性能曲线整体略有提高，这是因为压比是约束条件而非优化目标。图15说明了原始和优化叶型子午面和叶轮及回流器叶片几何型线变化。图16和图17进一步展示了子午面和50%叶高截面熵分布对比。可见优化后，原叶轮区域的轮盖侧转折处以及出口弯头处的流动分离消失，使其熵增减小，而叶片吸力面从前缘到尾缘的熵增均明显减小，表明优化后使得这些区域的流动损失降低，因此效率提高。

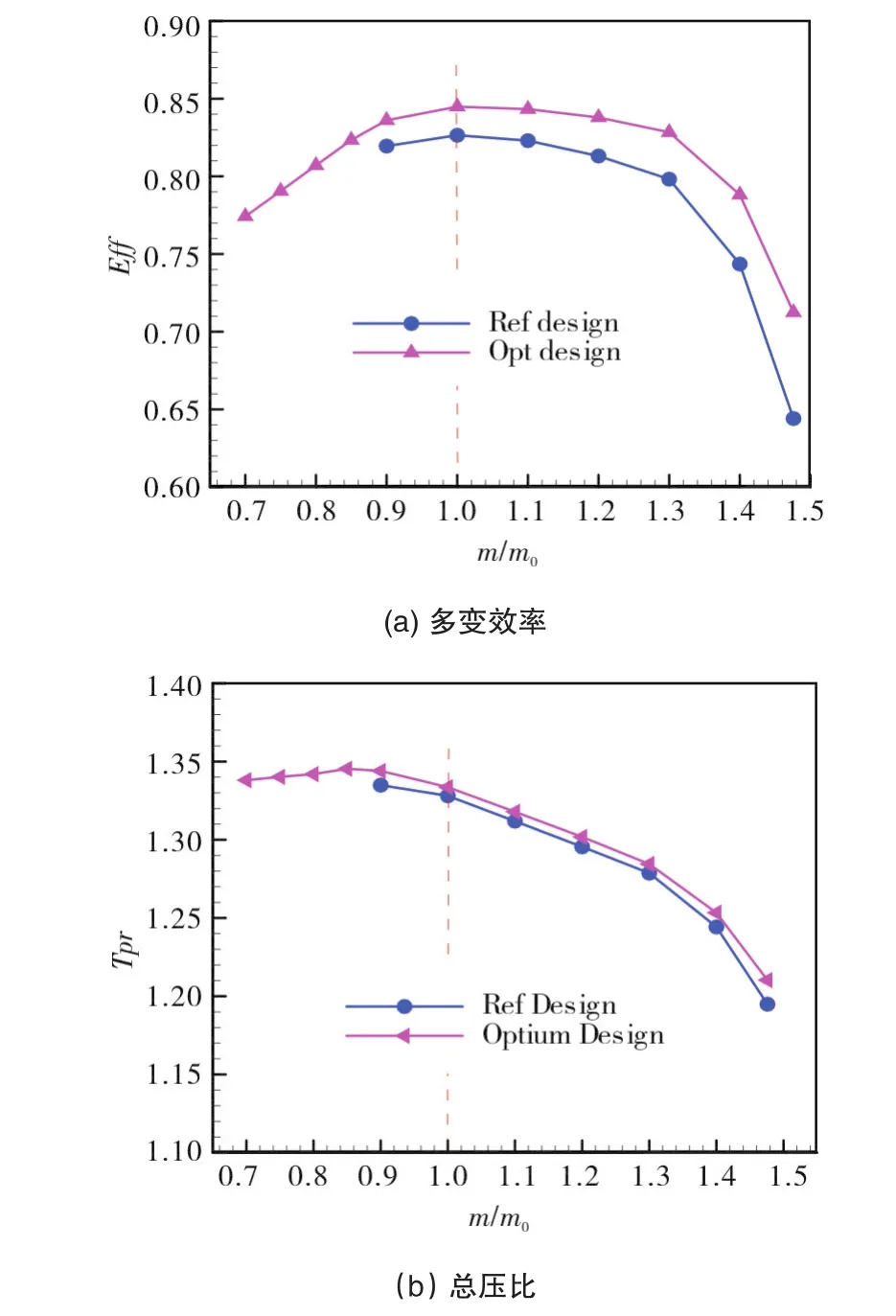
图14 模型级优化性能曲线对比Fig.14 Performance curve comparisons of original and optimized model stages

图15 优化前后叶轮和回流器叶片几何对比（黑色为原始叶型，紫色为优化叶型）Fig.15 Geometry comparisons of original(black line)and optimized(purple line)impellers and reflux blades

图16 子午流道熵和流线分布Fig.16 Entropy and streamline distributions in meridian plane

图17 50%叶高截面熵分布Fig.17 Entropy distributions in mid-span section

通过上述优化性能及详细流场参数对比分析，在说明性能提升原因的同时，也说明局部的低速流动分离结构会对模型级变工况运行能力产生显著影响，尤其是多级压缩机设计时更需要关注流场结构的控制。此外，优化工作进一步验证了该自动优化系统的可靠性，既可以用于新模型级开发，也可以作为通用平台进行现有二元叶轮级的性能优化。

5 结论

本文以某大型化工压缩机中的典型二元叶轮级为研究对象，建立了通用的整体结构参数化设计方法，基于改进后的高效全局优化算法和经验验证的CFD求解修正技术开发了二元叶轮模型级优化设计系统，开展了典型参数高效模型级设计和现有产品二元叶轮级扩稳优化研究，得到如下结论：

1）二元叶轮模型级参数化设计方法充分考虑气动性能需求和工艺要求，共涉及50多个变量参数，可以实现模型级的准确造型，且该方法稳健、通用。

2）本文结合Kriging响应面模型开展了优化算法改进，研究了基于多点搜索的MSEGO全局优化算法，经验证，在优化结果准确性方面远优于EGO算法。在此基础上提出了高效优化逻辑和过程控制方法，并结合CFD数值求解技术建立了模型级优化设计和分析系统，实现了优化迭代、数值计算与分析的全自动进行。

3）基于本文建立的优化设计系统，开展了典型参数模型级设计，在设计工况效率达到83%以上的同时，能够实现60%～120%流量工况高效稳定运行，达到行业同类产品先进水平。同时该系统能够有效实现对现有产品二元叶轮级自动优化，结果表明优化后通过抑制叶片吸力面、轮盖转折处及出口弯头处等局部区域的低速分离结构，不仅将设计工况效率提高1.84%，近堵塞工况效率提高6.83%，而且还将失速流量从90%设计流量降低至70%设计流量，有效拓宽了可靠运行范围，从而为高效模型级设计和优化提供了可靠的技术支撑。