叶根金属法兰对风电机组叶片螺栓疲劳性能的影响分析

刘作辉 田凤帅 庄恒东

（1.华锐风电科技（集团）股份有限公司；2.锐源风能技术有限公司）

0 引言

近几年，我国的风电行业发展迅猛，风电机组的质量安全也越来越受重视。螺栓作为风电机组的主要连接方式之一，应用在叶轮、轮毂、齿轮箱等诸多关键部位，其安全关系到整个风电机组的安全可靠运行[1]。其中叶片螺栓是连接叶片金属法兰、风机叶片及变桨轴承之间的连接部件。其中叶片金属法兰在连接系统中起调整作用，在设计过程中往往不被重视。某风场客服反馈，风电机组叶片螺栓存在疲劳断裂现象。通过对叶片连接系统进行有限元分析，发现叶片金属法兰是影响螺栓疲劳寿命的因素之一。本文系统的介绍了螺栓疲劳寿命的计算方法，量化分析了叶片金属法兰对叶片螺栓寿命的影响。为后续风机连接系统的设计及优化提供切实可行的方法和依据。

1 叶片螺栓疲劳计算方法及流程

螺栓疲劳计算主要流程如图1所示，其中主要分为螺栓的静力学有限元分析和螺栓的疲劳计算。螺栓的静力学有限元分析主要包括：几何建模、材料设置、网格划分、载荷及边界条件、求解参数的设置、有限元求解。螺栓的疲劳计算主要包括：螺栓的应力提取、螺栓载荷与应力幅映射、螺栓S-N曲线计算、螺栓疲劳累计。

1.1 几何模型与网格模型

叶根连接系统主要包含：叶片金属法兰、叶根、变桨轴承、T型螺母、双头螺柱、六角螺母、垫片、轮毂以及轮毂螺栓。采用三维软件建立几何模型，叶根连接系统的剖视图如图2所示。将叶根连接系统的几何模型保存成Parasolid格式文件，然后导入到有限元软件中。

图2 叶根连接系统几何模型Fig.2 Geometric model of blade root connection

将叶根连接系统离散成有限个单元体，这些单元体在节点处相互连接，叶片金属法兰、叶根、变桨轴承、T型螺母、双头螺柱、六角螺母、垫片、轮毂、轮毂螺栓，均采用Solid186、187单元（高阶单元）；螺栓预紧力采用Prets179单元。部件之间接触采用软件中Connection Group工具实现自动生成接触对。双头螺柱与T型螺母、六角螺母以及轮毂螺栓与轮毂设置成Bonded类型接触；其余各部件之间接触设置成Frictional类型接触，摩擦系数设置为0.2。叶根连接系统及单个叶根螺栓网格如图3所示。

图3 叶根连接网格模型Fig.3 Root connected grid model

1.2 材料属性与载荷

叶片金属法兰、变桨轴承、T型螺母、双头螺柱、六角螺母、垫片、轮毂、轮毂螺栓材料参数见表1所示，螺栓的屈服应力为940MPa。叶根为复合材料，X方向为叶片轴向方向，而Y方向为叶根周向，Z方向为根部铺层厚度方向。创建叶根单元坐标系，调整叶片根部单元主方向与材料主方向一致，等效复合材料如表2所示。

根据Blade模型计算出叶片根部极限载荷为M=10 600kNm。轮毂螺栓的预紧力为360kN，叶片螺栓预紧力为390kN。

表1 材料参数Tab.1 Material parameters

表2 等效复合材料参数Tab.2 Equivalent composite parameters

1.3 有限元求解设置

在求解设置时，需要涵盖叶片根部所有疲劳载荷。计算时取其极限载荷，包络叶根疲劳载荷，分别进行正向载荷Mx=10 600kNm和负向载荷Mx=-10 600kNm两种工况的计算，实现叶根载荷从-10600kNm至10600kNm之间覆盖。

对叶根进行静力学求解。为了防止极限载荷加载和预紧力加载相互影响，导致计算结果精度的降低。将求解设置分为两步，即第一步为加载螺栓的预紧力，第二步为加载外载荷。在加载外载荷时，分为10个子载荷步，每个载荷步保留并输出计算结果。

1.4 螺栓应力幅提取

螺栓应力幅为叶根螺栓在预紧力的作用下，叶根有工作载荷和无工作载荷的螺栓光杆处应力的差值。载荷存在正负，应力幅也存在正负。正向应力幅表示螺栓应力增加幅度；负向应力幅表示螺栓应力减少幅度。

有限元计算结果中，在图3中位置中的螺栓应力幅最大，以该处螺栓应力幅计算螺栓疲劳寿命最安全。采用软件中Bolt tool螺栓后处理工具，将该螺栓的每个载荷步下Working Load的受力提取出来，再除以螺栓光杆处截面积，得到螺栓的应力。将各个载荷步下螺栓应力与0外载荷时的螺栓应力做差，得螺栓的应力幅。并对其进行外载荷与应力幅曲线拟合。以叶片金属法兰23mm为例。提取各种载荷下螺栓受力、应力幅，如表3所示。将叶片螺栓不同载荷下的螺栓应力幅与载荷，采用5次多项函数拟合函数进行拟合，形成载荷-应力幅拟合函数。如图4所示。

图4 多项式拟合载荷-应力幅曲线Fig.4 Polynomial fitting of load stress gradient curve

表3 叶片法兰厚23mm，螺栓应力幅Tab.3 Blade flange thickness 23mm，bolt stress gradient

1.5 螺栓载荷频次与应力幅映射

通过拟合的螺栓载荷—应力幅曲线，实现任意载荷下的螺栓应力幅的插值计算。根据叶根的疲劳载荷（每隔15°的Markov二元矩阵，元素的每一个元素即载荷范围出现频次），计算螺栓的疲劳损伤。其主要过程为：建立螺栓载荷频次与螺栓应力幅度之间对应关系。如图5所示，Markov疲劳载荷矩阵中横坐标为载荷范围，纵坐标为平均载荷值，每一个元素为发生频次。建立应力幅度与频次一一对应关系的具体过程如下：疲劳载荷矩阵[500,1 200]元素对应最小载荷（Smin）为-100,最大载荷（Smax）为1 100。将最小载荷与最大载荷带入载荷应力幅插值函数中，计算求出[500,1 200]元素对应的应力变化幅度。建立载荷出现的频次与应力幅对应关系。矩阵中的每一个元素，采用同样的方法进行建立载荷频次与应力幅度的一一对应映射关系。

图5 最大载荷与最小载荷计算Fig.5 Calculation of maximum load and minimum load

1.6 螺栓S-N曲线

根据GL[2]规范及BS-EN-1993-1-9[3]计算螺栓疲劳S-N曲线。根据参考GL[2]标准，螺栓经过热处理的公式：

Fsmax为极限载荷下螺栓的最大力，F0.2min为0.2%的弹性拉力极限下的螺栓力，因此选择85MPa的应力范围作为M36螺栓S-N曲线的参考值，根据BS-EN-1993-1-9[3]，可计算出在NR=5×106条件下的，为σR=62.6MPa。同时需要考虑螺栓尺寸对S-N曲线的影响，对尺寸＞M30的螺栓，需增加系数Ks，计算方法见公式：Ks=(30/d)0.25，其中：d为名义直径，此计算模型中，d=36mm。材料部分安全因子取1.15。因此，在NR=5×106条件下，ΔσR的最终值为52.03MPa。螺栓的SN曲线如图6所示。

图6 螺栓的S-N曲线Fig.6 S-N curve of bolt

1.7 Miner螺栓疲劳损伤累积

Miner线性累积损伤理论被工程界广泛采用。材料在各个应力幅下的疲劳损伤是独立的，总损伤可以线性累加。假设某一级别应力幅σ1作用n1次，在该应力水平下材料达到破坏的循环次数为N1，该部分应力循环对结构造成的疲劳损伤为n1/N1，如图7所示。

图7 等效应力幅与频次Fig.7 Equivalent force amplitude and frequency

总损伤D是各级应力幅的损伤和：

基于1.5节中建立起的载荷频次与应力幅度的对应关系，利用材料S-N曲线，求出Markov疲劳载荷表中每一个元素对应的许用频次N。将Markov疲劳载荷矩阵每个元素对应的损伤进行累加，最终得到螺栓疲劳损伤。

2 叶片金属法兰对叶片螺栓寿命的影响

影响叶片螺栓疲劳寿命的因素有很多。例如在叶片螺栓加工过程中采用先调质后滚牙的螺栓加工工艺[4]；螺栓在使用过程中在保证极限工况安全的前提下，提高螺栓的预紧力[5]，这些方法都可以提高螺栓的疲劳寿命。相反如果叶根金属法兰存在间隙，螺栓连接体刚度降低，造成叶片螺栓疲劳断裂[6]。本文仅以叶片金属法兰的厚度为研究对象，分析其对叶片螺栓寿命的影响。

2.1 叶片金属法兰对叶片螺栓应力幅的影响

采用第1章节的计算流程及计算方法，计算不同叶片金属法兰厚度的叶片螺栓疲劳寿命。方法不再重复叙述。不同法兰厚度的螺栓寿命的影响主要参数为螺栓的应力幅变化。当螺栓应力幅变化较小时，螺栓的疲劳损伤最小，螺栓寿命最长。将不同叶片金属法兰厚度下的螺栓应力幅汇总成应力幅表，其载荷-应力幅曲线如图8所示。

图8 螺栓载荷-应力幅曲线Fig.8 Stress gradient curve of bolt

从图中可以看出：28mm法兰厚度时螺栓的应力幅最小，23mm及30mm的螺栓应力幅均大于28mm的螺栓应力幅。其应力幅的变化规律为：法兰厚度从23mm至30mm，叶片螺栓应力幅变化为先减小，再增大；其中叶片金属法兰28mm对应的叶片螺栓应力幅最小。

2.2 叶片金属法兰对叶片螺栓寿命的影响

根据螺栓S-N曲线、螺栓最大应力幅及螺栓Markov疲劳载荷，计算叶根每间隔15°方向下的螺栓疲劳损伤。如图9所示，其周向坐标为叶根每间隔15°。其径向坐标为螺栓的损伤值。各个角度下螺栓损伤如表4所示。从图9中可以看出：当45°时，螺栓的损伤最大，以此角度下的螺栓损伤是否满足螺栓的设计要求的评判依据。从结果可以发现，金属法兰的厚度为28mm时，螺栓损伤最小。29mm,30mm法兰厚度的螺栓损伤均超过28mm。计算结果表明：法兰厚度不是越厚越好，当法兰厚度达到一定程度时，螺栓的疲劳损伤最小，此时螺栓的使用寿命最长，超过此厚度时，螺栓的疲劳损伤逐渐增加。

图9 螺栓的损伤值Fig.9 Damage value of bolt

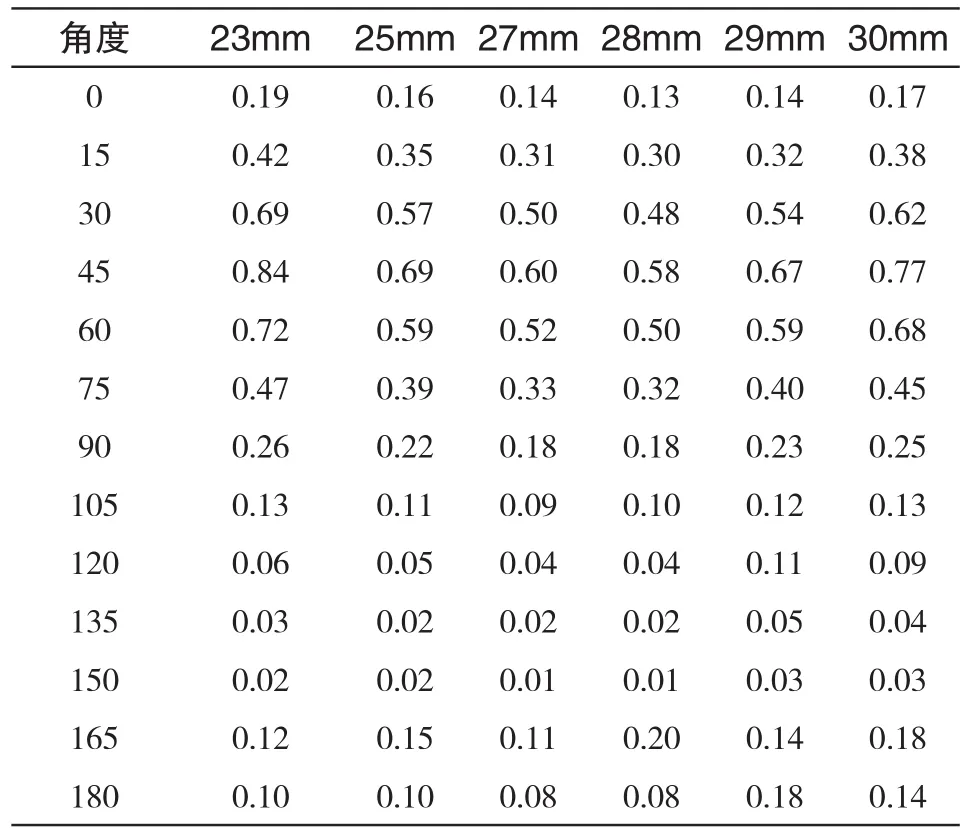
表4 不同厚度叶片金属法兰损伤Tab.4 Damage of root metal flange with different thickness

3 结论

本文详尽的介绍了叶片螺栓的计算流程及方法，阐述有限元计算的相关参数设置、S-N曲线的选取与计算、螺栓损伤的累积计算。并以某叶根连接系统为例，计算出不同金属法兰厚度的螺栓的损伤。计算结果表明：某机组叶片金属法兰的最优厚度为28mm。叶片金属法兰厚度从23mm增加到30mm，叶片螺栓损伤呈现出先减小在增大的规律。即开始时，螺栓疲劳损伤随法兰厚度的增大而减小；当螺栓疲劳损伤达到最小时，随着法兰厚度的增大，螺栓的损伤反而逐渐增大。