基于Collatz-Wielandt函数的不可约非负矩阵最大特征值算法
2020-09-27吕洪斌张美黎商钰莹王信存
吕洪斌, 张美黎, 商钰莹, 王信存
(1. 北华大学 数学与统计学院, 吉林 吉林 132013; 2. 辽东学院 师范学院, 辽宁 丹东118003)
1 预备知识
非负矩阵在计算数学、 线性规划、 计算机科学、 自动控制等领域应用广泛[1-3], 在与其密切相关的不可约M-矩阵、 对角占优矩阵的判定中具有重要作用[4], 非负矩阵最大特征值的估计[5-7]与计算[4,8-10]是非负矩阵理论中的经典内容.
Hn={x=(x1,x2,…,xn)T:xi≥0,i=1,2,…,n}{0},
设A=(aij)∈Mn(+), ∀i∈N, 记: det(λE-A)=0}表示矩阵A的谱集;表示矩阵A的谱半径. 由Perron-Frobenius定理[1,4]知, 若A∈Mn(+), 则r(A)∈σ(A), 称为矩阵A的最大特征值; 其对应的特征向量可取为非负向量, 称为矩阵A的最大特征向量. 进一步, 当A∈Mn(+)不可约时, 称r(A)为不可约非负矩阵A的Perron根, 其对应的正特征向量称为矩阵A的Perron向量[1,11].
定义1[1,11]设矩阵A=(aij)∈Mn(), 如果存在n阶置换矩阵P, 使得
则称矩阵A是可约的, 否则称矩阵A是不可约的, 其中A11为r×r阶矩阵(1≤r 定理1[11-12]设A∈Mn(+)不可约,r(A)是A的谱半径, 则: 定理2[11-12]设A=(aij)∈Mn(+),r(A)是A的最大特征值, 则 目前, 关于不可约非负矩阵最大特征值的计算主要有基于矩阵正对角相似变换下的算法[8-9]及应用非负矩阵的Collatz-Wielandt(C-W)函数算法[10]. 设A∈Mn(+)不可约,r(A)是A的最大特征值, 由文献[11]知, 则问题将被简化. 本文利用非负矩阵的C-W函数, 给出一种求不可约非负方阵最大特征值和最大特征向量的数值算法, 由于每一步迭代都可根据实际选择一个适合的参数, 因此算法具有简单和收敛快的特点. 定义2[11-12]设A=(aij)∈Mn(+)不可约, (1) FA(x)和GA(x)为两个从Hn到+的函数. 定义GA(x)=+∞, 若存在某个i, 使得xi=0且(Ax)i≠0, 则称其为伴随于矩阵A的Collatz-Wielandt函数, 简称为矩阵A的C-W函数. 定理3(C-W定理)[12]设A=(aij)∈Mn(+)不可约,FA(x),GA(x)是A的C-W函数, 则: 1)FA(x)和GA(x)都是零次齐次式; 2) 如果d是满足Ax-dx≥0(x∈Hn)的最大实数, 则d=FA(x); 如果e是满足Ax-ex≤0(x∈Hn)的最小实数, 则e=GA(x); 3) 如果x∈Hn, 且y=(E+A)n-1x, 则FA(y)≥FA(x),GA(y)≤GA(x); 4)FA(x)≤s,GA(x)≥t, 其中s,t分别为A的最大、 最小列和. 设A=(aij)∈Mn(+)不可约,则当m≥n-2时Bm为正矩阵[12]. 对任取的初始向量x(0)∈Hn, ‖x(0)‖∞=1, 定义如下迭代格式: (2) 定理4设A∈Mn(+)不可约,为由迭代格式(2)定义的向量序列, 则 证明: 由C-W函数的定义式(1), 对任意k=0,1,2,…, 有 Ax(k)-FA(x(k))x(k)≥0, 于是, 当k≥m时有 BmAx(k)-FA(x(k))Bmx(k)≥0. 因为ABm=BmA, 故有 A(Bmx(k))-FA(x(k))(Bmx(k))≥0, 进而得 Ax(k+1)-FA(x(k))x(k+1)≥0. (3) 由定理3中2)得 FA(x(k))≤FA(x(k+1)),k=m,m+1,…, 由定理3中4)知{FA(x(k)):k=m,m+1,…}是有上界的单调不减非负实数列, 从而存在极限. 又由定理3中4)及A不可约知, 知 Au-au>0, 注1若A∈Mn(+),aii>0(i=1,2,…,n), 为提高收敛速度可取αi<0, 满足 注2由迭代格式的构造及定理4的证明过程知,m可取为满足m≥n-2的任意正整数, 因此可把式(2)进一步优化为: x(k)=y(k)/‖y(k)‖∞,k=1,2,…. 算法步骤如下: 4) 输出特征值r(A)=(GA(x)+FA(x))/2及特征向量x. 注3算法中的参数α可根据实际情况进行选取. 下面应用MATLAB软件分析上述算法. 例1 分别利用本文算法(取αi=rmax-rmin-n)和文献[4,8]的算法计算r(A6)的迭代次数, 对比结果列于表1. 其中应用本文算法、 文献[4]算法、 文献[8]中算法9计算r(A6), 每一步迭代所需的乘法、 除法和加法运算次数基本相同. 由表1可见, 在迭代次数上本文算法具有明显优势. 表1 不同算法计算矩阵A6的最大特征值迭代次数比较 例2 表2 不同算法计算矩阵A的最大特征值迭代次数比较 由表2可见, 本文算法的迭代次数是文献[8]和文献[9]算法的1/2和1/4次, 但其乘法、 除法和加法的运算次数基本相同, 再次表明了本文算法的优势.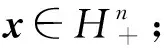
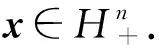

2 主要结果
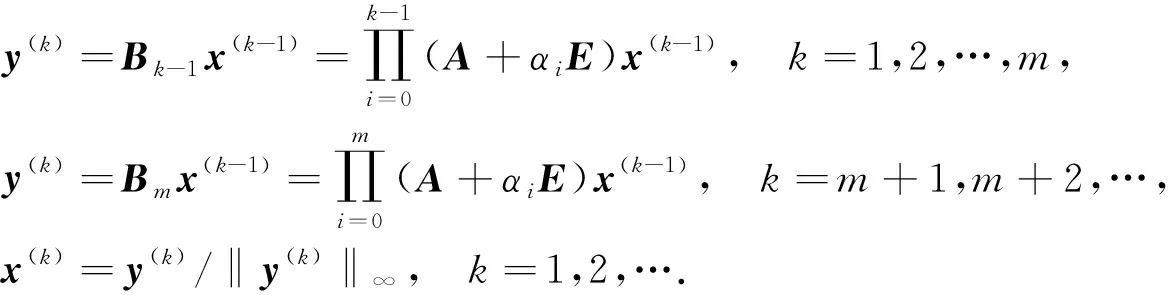

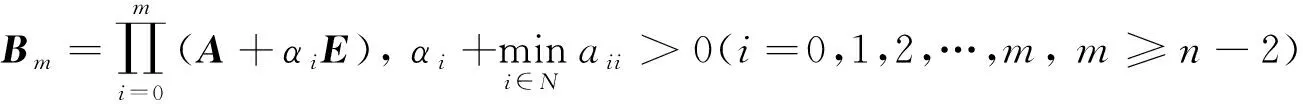


3 数值算法及分析