基于PCA-BN的银川市空气质量预测
2020-09-27穆春阳
卢 彬,马 行,穆春阳,张 鄂
(1.北方民族大学宁夏智能信息与大数据处理重点实验室,宁夏 银川 750021;2.北方民族大学电气信息工程学院,宁夏 银川 750021;3.北方民族大学机电工程学院,宁夏 银川 750021)
近年来,空气质量问题成为了全社会广泛关注的焦点问题,空气质量状况影响着人们的日常生活出行和当地社会生产活动。因此,空气质量的预测对当地大气污染监管和治理有着重要的意义。
我国学者杨瑞君等[1]将随机森林(BF)模型引入上海市空气质量的评价中,结果表明BF模型在空气质量等级的评价中有较高的准确率;化虎蝶等[2]将贝叶斯网络(BN)引入到大连市的空气质量评价与预测中,并与模糊综合评价法的预测结果进行对比,结果表明BN法在预测精度上有显著的提高。这些研究虽对城市空气质量的预测提供了可靠、准确的方法,但未考虑气象因素对城市空气质量的影响。杨正理等[3]将影响城市空气质量的34种气象因素作为输入,将互信息与BF算法引入太原市空气质量的预测中,结果表明该方法能够有效识别影响城市不同区域空气质量的气象因素,并在城市空气质量预测上有较高的可靠性和准确率;郭飞等[4]将温度、气压、湿度、风速4种气象因素作为输入,并将改进的支持向量机(Support Vector Machine,SVM)应用于沈阳市空气质量预测中,结果表明改进后的SVM有效地降低了预测错误率,提升了预测精度。这些研究虽然考虑了气象等因素对城市空气质量的影响,但未对气象等因素进行信息的浓缩,当因素较多时,因素之间可能存在信息的重叠和相关性,从而增加模型结构和数据分析的复杂度[5]。
为了解决上述研究中所存在的问题,本文结合主成分分析(PCA)方法对数据降维以消除信息冗余的特点以及BN在多因素复杂系统中具有较强推理能力的优势[6],以银川市2015年1月1日至2019年10月31日的空气质量数据和同期的气象数据为基础,将PCA-BN模型引入到银川市空气质量的预测中,建立了基于PCA-BN的银川市空气质量预测模型,并对模型预测准确率以及可靠性和可行性进行了验证。
1 数据来源与研究方法
1. 1 数据来源
本文通过网络爬虫爬取银川市2015年1月1日至2019年10月31日的空气质量等级、空气质量指数以及空气中细颗粒物(PM2.5)、可吸入颗粒物(PM10)、二氧化硫(SO2)、一氧化碳(CO)、二氧化氮(NO2)、臭氧(O3)6种主要污染物浓度数据和同期的气象数据日均值。其中,同期的气象数据主要包括平均地表气温、日最高地表气温、日最低地表气温、平均相对湿度、日照时数、平均气温、日最高气温、日最低气温、平均气压、平均风速10项指标。空气中6种主要污染物浓度数据的时间序列图见图1,10项气象指标数据的时间序列图见图2。
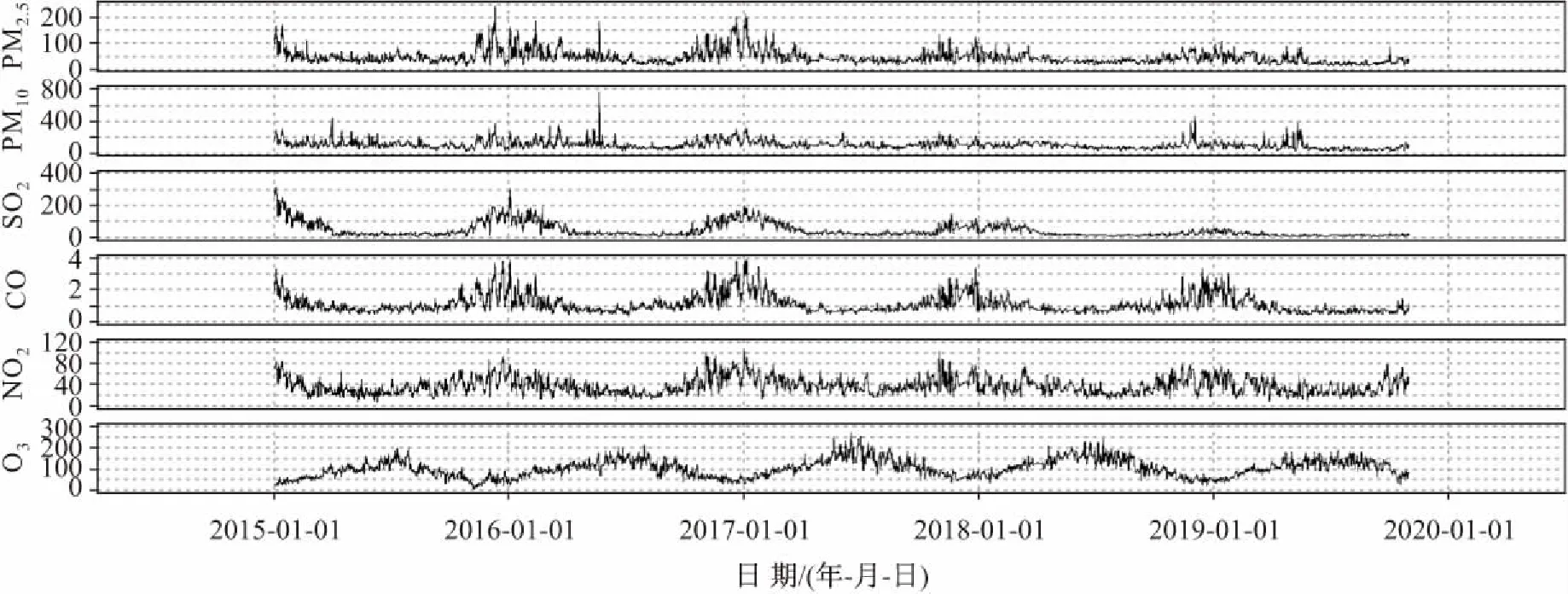
图1 2015年1月1日至2019年10月31日银川市空气中6种主要污染物浓度数据的时间序列图(单位:μg/m3)Fig.1 Time series diagram of the content data of six major pollutants in the air of Yinchuan City from Jan 1st, 2015 to Oct 31st,2019(unit:μg/m3)
1. 2 研究方法
本文研究方法分为三个步骤进行:①对1 765条样本数据进行数据清洗,处理样本数据中存在的缺失值;②利用主成分分析方法对气象数据进行降维处理并提取气象因素的综合评价指标;③构建基于PCA-BN的银川市空气质量预测模型。
1.2.1 数据清洗
首先对1 765条样本数据进行数据清洗,处理样本数据中存在的缺失值。由于样本数据中存在缺失值的数据量占样本数据总量的比例较小,因此对样本数据中连续缺失的数据做剔除处理,对于一个有数据缺失的缺失值, 采用相邻日期前后两项数据的平均值进行插补。将经过数据清洗后得到的1 677条数据作为新的样本数据,以样本数据中的70%作为训练数据集,30%作为验证数据集,构建PCA-BN模型。
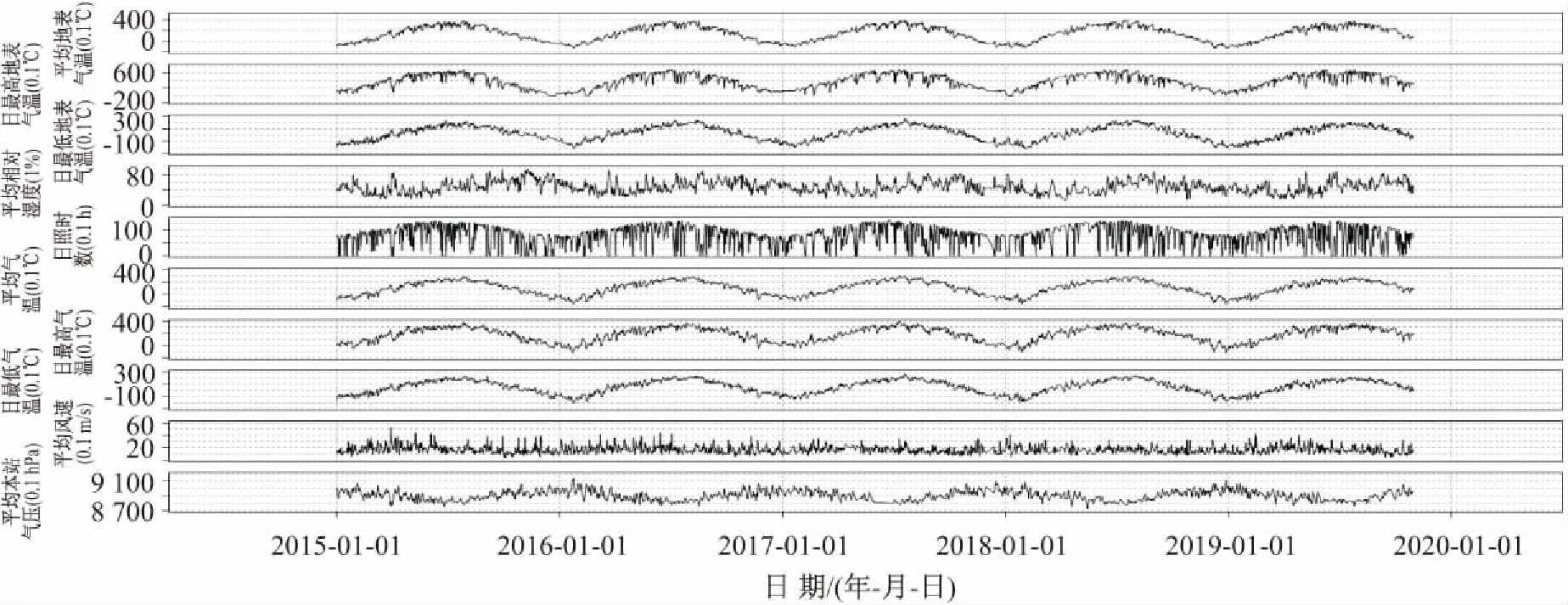
图2 2015年1月1日至2019年10月31日银川市10项气象指标数据的时间序列图Fig.2 Time series chart of the content data of ten meteorological indicators of Yinchuan City from Jan 1st, 2015 to Oct 31st,2019
1.2.2 主成分分析
主成分分析(Principal Component Analysis,PCA)方法常用于处理变量之间具有高度相关性的数据[7]。该方法是运用降维的思想去除冗余的信息,将多个变量转化为由多个变量线性表示的少数主成分的过程[8]。根据PCA原理,可分为如下几个步骤进行计算[9]:
(1) 对数据进行标准化处理:
(1)
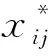
(2) 计算相关系数矩阵R=(rjk)m×m:
(2)

(3) 求解相关系数矩阵的特征值与特征向量。
(4) 提取主成分:主要根据特征根和累计贡献率的值来提取主成分,一般选取特征根大于1的主成分[10]。主成分zt的方差贡献率wt为
(3)

wt值越大,表明主成分Zt对原始变量信息的解释能力越强。前q个主成分的累计方差贡献率Wq为
(4)
Wq表示所提取的q个主成分能够解释原始变量信息量的多少。
1.2.3 贝叶斯网络
贝叶斯网络(Bayesian Networks,BN),又称信度网络,是一种结合了概率论和图论的不确定性知识表达与推理的方法。BN作为一种图形化模型,能够表达出因果关系和相关的不确定性知识,该模型由节点、有向弧和条件概率表(Conditional Probability Tables,CPT)组成[11-12]。由于BN要求各节点之间不能形成闭环,因此BN符合有向无环图(Directed Acyclic Graph,DAG)结构[13]。BN因其具有的简洁、直观、准确、方便的特点,在实际工程中得到了广泛的应用[14]。在BN中,贝叶斯公式为概率计算的基础,贝叶斯公式[15]如下:
(5)
其中P(Xi)>0,P(E|Xi)>0,P(Xi|E)>0。
式中:X1,X2,…,Xn为样本空间Ω中两两互斥的事件;P(Xi)为事件Xi的先验概率[16];P(Xi|E)为后验概率,表示在已知事件E发生的概率下,事件Xi发生的概率;P(E|Xi)为条件概率,表示在已知事件Xi发生的概率下,事件E发生的概率。
BN的学习分为BN的结构学习和BN的参数学习。其中,BN结构学习是根据数据经验和先验知识确定BN结构,在得到确定的BN结构的基础上,采用合理的参数学习方法确定BN拓扑结构中各节点之间的条件概率[17];BN参数学习是以BN结构为基础,如图3所示为一个简单结构的BN结构图,根据先验概率、后验概率以及条件概率等知识对构成BN结构的各节点进行定量分析,并得到各节点间相关关系的强弱[18]。

图3 简单结构的贝叶斯网络(BN)结构图Fig.3 Diagram of Bayesian Network (BN) with simple structure
如图3所示,节点X1、X2均通过有向线段指向节点Y,有向线的起点为子节点,终点指向父节点,利用参数学习方法可分别求得父节点Y与各子节点X1、X2的条件概率。
为了提高BN局部因果结构的效率并有效地对原始变量的特征空间进行降维,本文利用马尔科夫毯(Markov Blanket,MB)算法进行BN结构学习。马尔科夫毯的定义为:集合U为随机变量的全集,对于一个给定的变量X(X∈U)和变量集MB(MB∈U且X∉MB),若满足[19]:
X⊥{U-MB-{X}}|MB
则称最小变量集MB为变量X的马尔科夫毯。
本文所采集的数据为各项指标的日均值且数据量充足、较为完整,故采用最大似然法作为BN结构的参数学习方法。假定数据集C={C1,C2,…,Cn},节点Xi共有hi个取值,且节点Xi的参数为θi,节点Xi的父节点α(Xi)的取值共有qi个组合,则节点Xi的参数θi的对数似然函数表达式如下[20]:
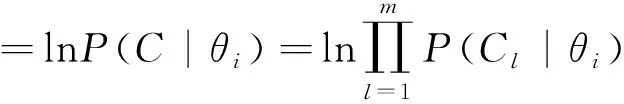
(6)
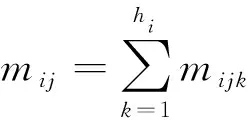
(7)
式中:mijk为数据集C中满足Xi=k且α(Xi)=j的样本数量。
2 研究结果与分析
2.1 PCA结果分析
本文利用PCA方法对银川市10项气象指标数据进行降维处理,得到KMO和Bartlett的球形度检验结果见表1。

表1 KMO和Bartlett的球形度检验结果
由表1可知,KMO的检验结果为0.790,大于0.500;Bartlett的球形度检验拒绝单位相关阵的原假设(Sig.<0.001),说明本文选取的10项气象指标数据适合进行主成分分析。
银川市10项气象指标数据经过PCA法降维处理后提取的3个主成分的方差百分比和累计方差贡献率,见表2。

表2 银川市10项气象指标数据经过PCA法降维处理后提取的3个主成分的方差百分比和累计方差贡献率
由表2可知,所提取的3个主成分解释了原10项气象指标数据信息量的91.563%,大于85%,说明提取的3个主成分是合适的。
银川市10项气象指标数据经过主成分分析后的碎石图,见图4。
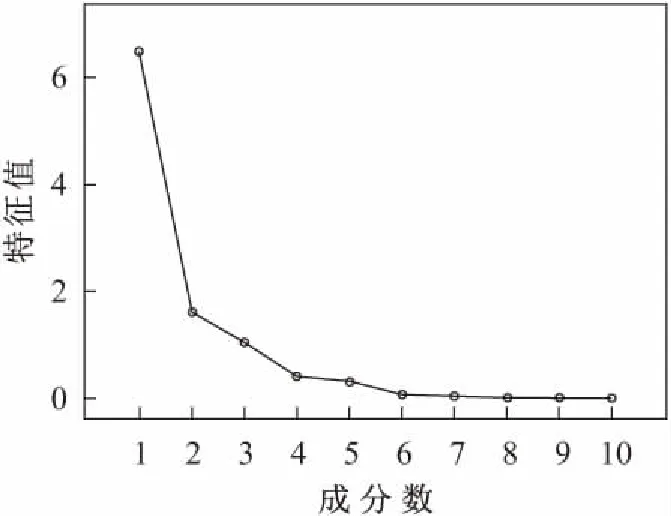
图4 银川市10项气象指标数据经过主成分分析后的 碎石图Fig.4 Scree plot in PCA analysis of ten meteorological indicators of Yinchuan City
由图4可见,第三个主成分之后,曲线变得平滑,没有出现明显的变化趋势,这从侧面说明PCA法将银川市10项气象指标数据降维处理后提取3个主成分是合适的。
由主成分因子负荷矩阵(见表3)可知,第一主成分主要包含原指标中各气温和平均气压指标,因此第一主成分可作为总体气温状况的综合描述指标;第二主成分主要包含原指标中平均相对湿度和日照时数指标,且平均相对湿度指标相较于日照时数指标在第二个主成分上具有更大的载荷,说明在第二主成分中平均相对湿度相比于日照时数具有更高的重要性,因此第二主成分可作为湿度状况的综合描述指标;第三主成分主要包含原指标中平均风速指标,因此第三主成分可作为风速状况的综合描述指标。
由表2和表3可知,第一主成分方差百分比较高,方差贡献率达到65.014%,说明气象因素中气温对空气质量有较大的影响。银川市10项气象指标的3个主成分序列图,见图5。
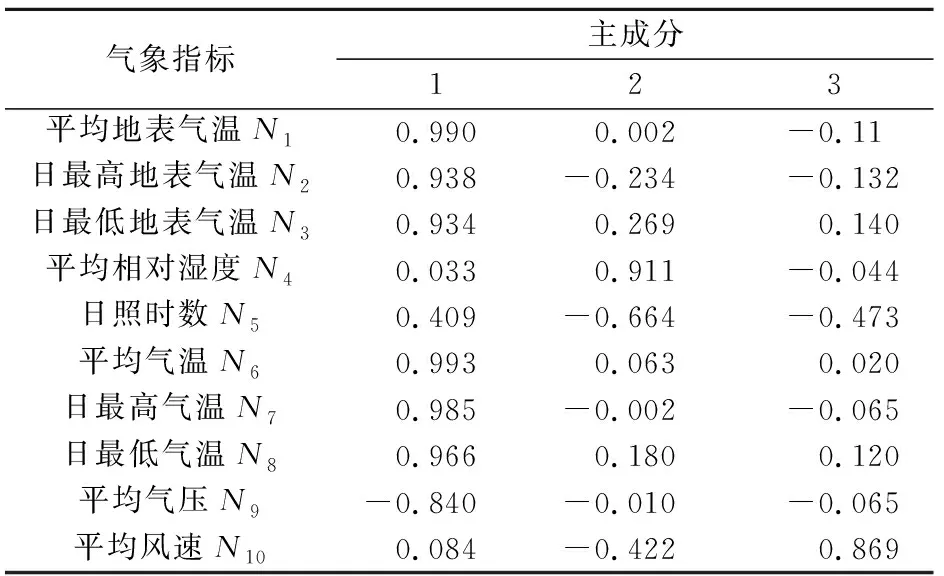
表3 主成分因子负荷矩阵

图5 银川市10项气象指标的3个主成分的序列图Fig.5 Sequence diagram of three principal components extracted from the ten meteorological indicators of Yinchuan City
2.2 构建PCA-BN模型
银川市原10项气象指标经过主成分分析后提取得到3项气象综合描述指标,不仅降低了气象指标的维数,并且反映了原气象指标的绝大部分信息量。以3项气象综合描述指标和大气中6项主要污染物浓度指标共9项指标数据作为输入,并对指标数据进行离散化处理,构建基于PCA-BN的银川市空气质量预测模型,即PCA-BN模型。
构建PCA-BN模型时,首先利用MB算法进行BN的结构学习。以质量等级为目标变量,先得到目标变量的MB;再根据目标变量的MB进一步确定所研究的预测变量的条件概率分布,由于目标变量的MB包含了目标变量的所有信息,则MB以外的变量可被视为冗余变量并排除了其余变量的影响[21];最后基于条件独立性测试判断两变量间是否相互独立,若相互独立,则删去连接两变量节点的线。
然后,利用最大似然估计进行BN的参数学习,确定每个变量的条件概率分布。PCA-BN模型中输入变量的重要性见表4,PCA-BN模型的网络结构图见图6,其中输入变量节点的颜色深浅表示预测变量重要性的高低。

表4 PCA-BN模型中输入变量的重要性
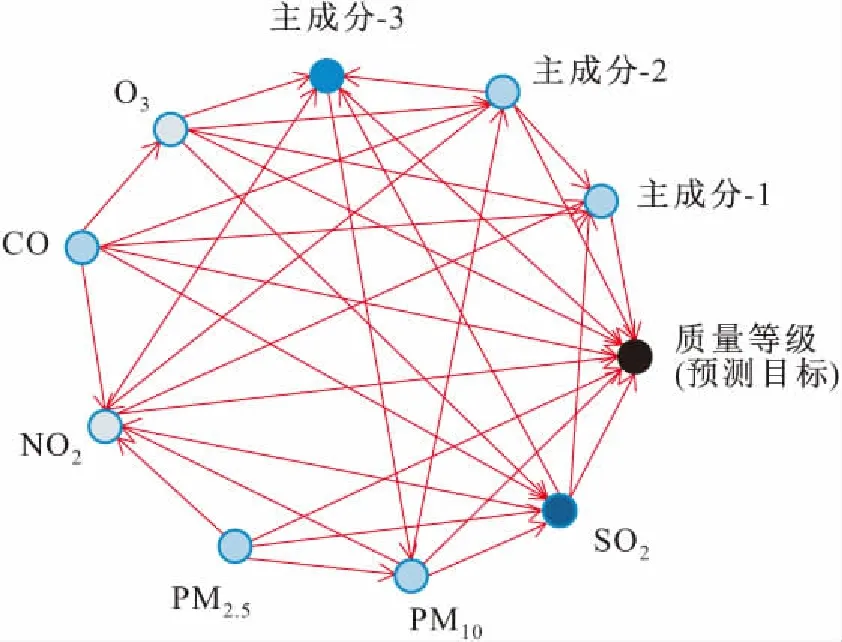
图6 PCA-BN模型的网络结构图Fig.6 Network structure diagram of the PCA-BN model
由表4和图6可知,PCA-BN模型中所输入的9项指标均会对银川市空气质量等级产生影响,且各项指标间也会有相互的影响关系。其中,SO2对于银川市空气质量的影响较大,故必须注意对于SO2污染源头的控制。
PCA-BN模型预测结果的准确率见表5。
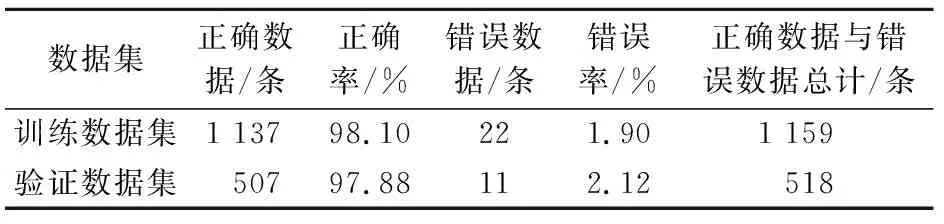
表5 PCA-BN模型预测结果的准确率
由表5可知,PCA-BN模型在训练数据集和验证数据集中的正确率接近,且预测结果的准确率达到97.88%。
PCA-BN模型预测结果的混淆矩阵见表6,其中行为空气质量实际值,列为空气质量预测值。
由表6可知,在验证数据集中,空气质量实际值为良的情况下,PCA-BN模型的预测值为轻度污染的个数为1个;空气质量实际值为轻度污染的情况下,PCA-BN模型的预测值为良的个数为2个,为中度污染的个数为3个;空气质量实际值为中度污染的情况下,PCA-BN模型的预测值为轻度污染的个数为4个,为重度污染的个数为1个;其余情况下均未出现预测错误。
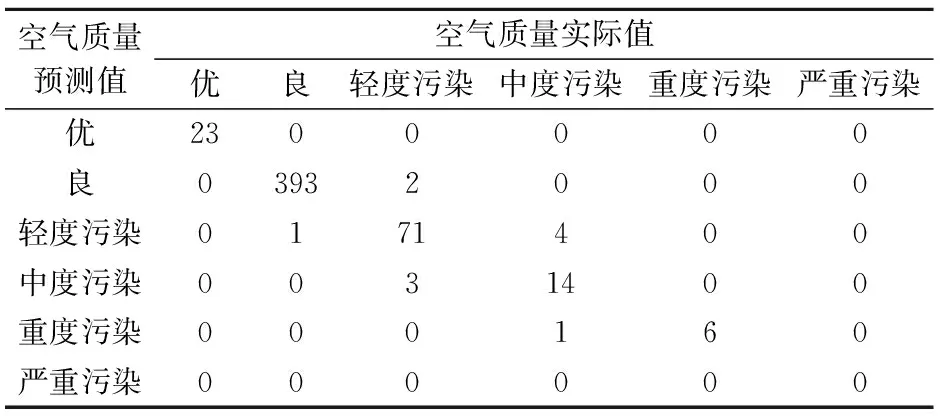
表6 PCA-BN模型预测结果的混淆矩阵
根据上述预测结果的准确率和混淆矩阵,说明PCA-BN模型在银川市空气质量的预测中有着较高的预测精度,具有一定的应用价值。
2.3 PCA-BN模型与随机森林模型预测结果的比较
为了进一步说明PCA-BN模型在银川市空气质量预测中的可靠性和可行性。本文利用随机森林(Random Forests,RF)模型并将空气中6种大气主要污染物浓度数据和同期的气象数据共16项指标作为输入,得到基于RF的银川市空气质量预测结果,并与基于PCA-BN模型的银川市空气质量预测结果进行了比较,其结果见表7。

表7 PCA-BN模型与RF模型预测结果的对比
由表7可知,RF模型和PCA-BN模型预测结果的准确率分别为88.03%和97.88%,PCA-BN模型对银川市空气质量预测结果的准确率有明显的提高,说明该模型在空气质量的预测中有一定的可行性和可靠性。
3 结 语
本文将PCA-BN模型引入银川市空气质量的预测中,结果表明:该方法预测结果的准确率达到了97.88%,并且有效降低了数据分析的复杂性。今后针对城市空气质量的预测还需要考虑更多的气象条件、区域环境、污染源排放、城市结构、城市发展水平等有可能影响到城市空气质量的因素,并提出合理的建议,以达到对空气质量状况更加准确的评价,促进城市空气质量的提升。
