基于核心素养的数学课堂教学实践

韩新方 李妍

[摘  要] 定积分是初等数学中建构完整知识体系不可或缺的内容，也是学生学习高等数学的认知基础. 为体现定积分应用的价值，文章基于对核心素养的理解进行教学设计，以解读并实践如何培养中学生的数学核心素养.

[关键词] 定积分应用;教学设计;数学核心素养

引言

随着《普通高中数学课程标准（2017年版）》的发布，“数学核心素养”一词便进入了中学教师的视野，并逐渐成了近期教学与研究的热点. 所谓数学核心素养，实质就是以数学知识为载体，使学生在数学学习和应用的过程中逐步树立正确的价值观念、必备品格，获得适应社会发展的关键能力[1]■. 可是对于大多数任课教师来说会有这样的疑问：如何在课堂教学中落实核心素养的培养？为此，笔者以“定积分的应用”这一节为例，探究如何在数学课堂教学中落实核心素养的培养.

“定积分的应用”教学设计

教学目标：（1）掌握利用定积分的几何意义求解平面面积的基本方法;（2）理解微元法的含义，会利用微元法求一般的立体图形的体积和表面积[2]■.

1. 问題设疑，引入新知

问题情境：有一椭圆花坛，经测量长度最长为2a米，宽度最宽为2b米，若对它进行绿化，需要多少平方米的绿植？

对于这个问题的处理，教师可以引导学生先由实际问题抽象出数学模型：以椭圆的中心为原点建立平面直角坐标系，则椭圆的标准方程为■+■=1. 借助椭圆的对称性，将问题转化为求位于第一象限内的曲边梯形的面积，或是x轴上方的曲边梯形的面积[3]■.

下面给出求解过程：

S椭圆=4■■dx=4b·■■dx.

由于被积函数是■的形式，因此采用三角换元法求解.

令x=acost，t∈0，■，则dx=d（acost）= -asintdt，根据牛顿—莱布尼兹公式有：

S■=-4ab■sint■dt= -4ab■sin2tdt=-4ab■■dt= -2ab（t-sin2t）■■=-2ab0-sin0-■+sinπ=πab.

发现：当a=b=r（常数）时，椭圆面积在形式上就转化为以常数r为半径的圆的面积公式. 可以发现当椭圆的长半轴长等于短半轴长，且两焦点重合时，椭圆就转化为圆，可以说圆是椭圆的“一般形式”.

设计意图：这一问题的设置基于学生的“最近发展区”，在激起学生求知欲的同时，达到引入新知以及温故知新的目的. 同时引导学生借助数学模型解决问题的过程，有助于培养学生数学抽象和数学建模的核心素养;在计算求解的过程中，又能够锻炼学生的数学运算能力. 最后，通过分析将圆与椭圆建立联系的过程，亦能很好地培养学生的逻辑推理能力和由一般到特殊的哲学素养.

2. 由浅入深，练习巩固

在上述“求椭圆花坛面积”的问题解决后，教师可以借由此题，和学生共同分析利用定积分的几何意义求解平面图形面积的过程，然后一起归纳、总结出求解步骤，在归纳的过程中提高学生的分析、总结能力，培养学生数学的抽象思维能力和归纳概括能力.

问题1：当函数图像与坐标轴的位置处于不同情况时[4]■，其面积公式是否有变化？

设计意图：由于学生已经知道当曲线完全位于坐标轴上方时的求解公式，但是在实际问题中，并不是所有的函数图像和坐标轴都有这样的位置关系，因此需要了解在不同情况下求解公式有什么不同的区别. 提出这一问题的目的主要是为了让学生自己思考，锻炼其发现问题和提出问题的能力，借此培养学生数学抽象的核心素养，渗透数形结合的思想方法.

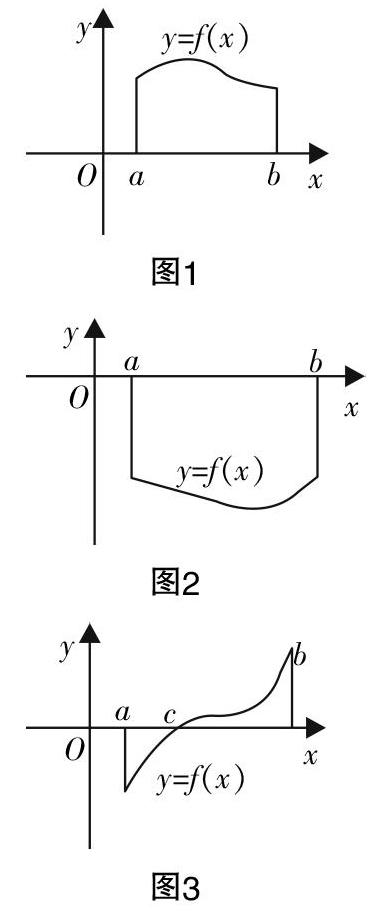
问题2：当函数y=f（x）与x轴的位置情况如下图所示（图1、图2、图3），应该如何求所围曲边梯形的面积？

解：由函数y=f（x）与x轴、直线x=a和直线x=b所围曲边梯形的面积S：

如图1所示，当f（x）>0时，S=■f（x）dx.

如图2所示，当f（x）<0时，S= -■f（x）dx.

如图3所示，当a≤x≤c时，f（x）≤0，当c≤x≤b时，f（x）≥0，S=■f（x）dx-■f（x）dx.

问题3：如下图所示（图4、图5、图6），如何求函数y=f（x）、函数y=g（x）与直线x=a和直线x=b所围曲边梯形的面积？

解：如图4所示，当f（x）>0，g（x）>0时，S=■[f（x）-g（x）]dx.

如图5所示，当f（x）<0，g（x）<0时，S=■[g（x）-f（x）]dx.

如图6所示，当f（x）>0，g（x）<0时，S=■[f（x）-g（x）]dx.

综上所述，可以得到S=■f（x）-g（x）dx.

设计意图：这部分内容的设置主要是为了引导学生从不同的平面图形中，抽象出相应的数学公式，以期利用其解决更广泛的数学问题. 锻炼学生用数学语言表达问题的能力时，培养学生思维的逻辑性和严谨性.

这一部分内容讲解结束后，设置相应的例题来让学生熟悉这些公式以及它们的适用情况. 可以通过让学生上黑板进行计算演示的形式提升学生的参与度，观察学生的掌握情况以及纠正他们所易犯的错误.

例1：计算由直线y=x-4，曲线y=■以及x轴所围图形的面积S.

解：（1）以x为积分变量：如图7所示，将所求图形面积分成两部分——S1和S2，为确定被积函数和积分的上、下限，需要求出两函数与坐标轴的交点以及两个函数的交点，则有S=S1+S2=■■dx+■■dx-■（x-4）dx=■x■■■+■x■■■-■（x-4）2■■=■.

（2）以y为积分变量：则需要将两函数转化为x=y+4和x=■，有S=■（y+4）-■dy=■y2+4y■■-■y3■■=■.

对于这个问题的第二种解法，需要任课教师稍加引导，让学生注意将积分变量转化后相应的函数解析式也需要进行变形. 同时比较两种解法，帮助学生体会通过转变积分变量，使得分割区域减少，进而大大减少运算量，也就是说，积分变量的选取需要依据实际问题[5]■.

3. 知识拓展，构建系统框架

在新课标中，定积分的知识作为供数理类、经济类和理工类学生所学习的内容，在知识层面上本就有一定的“拔高”性，因此在教学时可以做适当的拓展，保证定积分知识的完整性、连贯性，以及它对高中知识框架的补充作用. 也就是说，在高中阶段学生应该获得利用定积分的相关知识证明立体几何中常用公式的能力，并能够对高中的知识框架体系进行拓展、完善，为学习大学微积分知识打下良好的基础. 在这一过程中，如果运用定积分的定义来严格证明的话，不可避免的要用到极限的定义等现代数学知识，因此这里引入微元法[6]■来暂时回避这一难点，而又保持了一定程度的严谨性和逻辑性.

微元法：

（1）微元法的适用情况：①待求的数学量S是与变量x的变化区间[a，b]有关的量;②待求的数学量S对于区间[a，b]具有可加性;③部分量ΔSi的近似值可表示为f（ζi）Δxi.

（2）微元法的使用步骤：①具体问题具体分析. 选取一个合适的变量（比如x）作为积分变量，并确定它的变化区间[a，b]. ②分割小区间，求出对应于这个小区间[x，x+dx]的部分量ΔS的近似值.如果能表示成[a，b]上的一个连续函数在x处的值f（x）与dx的乘积，就把f（x）dx称为量S的元素，记作dS，即dS=f（x）dx. ③以所求量S的元素f（x）dx为被积表达式，得定积分S=■f（x）dx.

例2：求椭圆■+■=1绕x轴旋转一周得到旋转椭球的体积V1■[7].

分析：体积V1在区间[-a，a]上具有可加性，当用平面x=x0和平面x=x0+Δx截椭球时，则得到宽度为Δx的小薄片，将小薄片近似地看为小圆柱，有部分量ΔV1的近似值可表示为πb21-■.

解：选取x为积分变量，则它的变化区间为[-a，a]. 用平面x=x0和平面x=x0+Δx截椭球，可得到宽度为Δx的小薄片（也就是V1的部分量ΔV1），将小薄片近似地看为小圆柱，有部分量ΔV1的近似值可表示为πb21-■，有dV1=πb21-■dx. 所以有V1=■πb21-■dx，有V1=■πb2·1-■dx=■π■（a2-x2）dx=■πa2x■■-■x3■■=■πab2.

设计意图：借助例题帮助学生理解抽象的微元法，为后续运用微元法解决其他立体图形的体积和表面积的问题打下知识基础. 问题中的椭球是由本节课开篇得到的椭圆经旋转得到的，保证了这部分知识的连贯性，也为学生学习如何应用微元法将所求量转化为定积分，提供了严谨的参考步骤.

教学活动：让全班学生分为两组，动手计算当椭圆■+■=1绕y轴旋转一周时得到旋转椭球的体积V2，以及更一般的椭球（无论用垂直于哪个轴的平面截椭球，其截面均为椭圆）的体积V. 观察V1，V2和V，分析三者的关系.

提出问题：在平面中椭圆和圆具有“一般”和“特殊”的关系，那在空间中是否也具有这样的关系呢？

一般的椭球体体积为■πabc，球的体积为■πr3，也就是说当椭球中的a=b=c=r（常数）时，就会得到球的体积公式. 换言之，球是椭球的“一般形式”.

这一部分活动的设置可以让学生在动手计算的过程中，熟悉运用微元法的步骤，感受由特殊到一般和一般到特殊的辩证统一思维;同时培养学生发现问题的意识以及逻辑推理能力，促进其数学抽象和逻辑推理能力的发展.

而后，引导学生分析圆柱、圆台和圆锥均可由平面图形经过旋转或者由一般到特殊的關系得到，进而可利用上述椭球体积的求法求得其体积公式. 而对于棱锥和棱台，则只需要直接运用微元法将“小长方体”看作其微元计算即可. 这部分内容可以留给学生探究，培养学生类比推理和举一反三的能力，如果学生不能够发现类比项之间的关系，就需要任课教师对学生稍加引导. 至于立体几何表面积的公式证明，只需要将其分割得到的微元近似看作圆台，然后按照微元法的步骤求解即可.

课程至此，期待搭建出定积分应用的基本知识框架，为大学继续学习微积分的相关知识打下基础，也对“无依无据”的常用公式进行了严谨的证明，补全高中立体几何的知识，培养学生学习和掌握知识的逻辑性和严谨性. 此教学设计既加深了学生的知识层次，又培养了学生严谨的数学逻辑推理能力，起到“温故知新”的作用，同时让学生收获学以致用的喜悦和成就感，感受数学知识的应用价值，培养了学生的学习兴趣和学科自信. 但作为一节课的内容来说，以上内容显得容量稍大，因此任课教师可以做适当的调整，留一部分公式的证明作为课后的思考题.

结语

笔者认为，落实培养学生数学核心素养，意在以数学知识为载体，提升学生知识技能等各方面的综合能力. 对于学生来说，就是要丢弃单方面接受知识的习惯，学会自己发现问题、提出问题，并在教师的指导下解决问题，而且要通过数学知识的学习，培养思维的逻辑性和严谨性;对于教师来说，则需要做到让学生知道知识的来龙去脉，让所有的知识尽可能有依有据，所学知识框架尽量完整严谨;同时要在知识传授的过程中以学生为本位，运用多种教学方法以及教学工具来辅助教学，提升学生解决问题的能力，在学习的过程中使学生学会思考，具有思辨精神，成为对社会发展有用之人[8]■.

参考文献：

[1]  中华人民共和国教育部制定. 普通高中数学课程标准（2017年版）[S]. 北京：人民教育出版社，2018.

[2]  姜咏梅. 谈高职院校数学说课——以定积分的应用为例[J]. 科教文汇（下旬刊），2014（12）.

[3]  杨勇素. 初等数学中定积分的应用[A]. 中学教育科研2018年第4期（总第227期）[C]. 甘肃省兰州第一中学，2018.

[4]  罗文军. 例谈在数学课堂教学中落实核心素养——以“定积分在几何中的应用”为例[J]. 中学数学，2018（07）.

[5]  马树燕，王海萍. 浅谈定积分应用——平面面积部分的教学设计[J]. 科学咨询（科技·管理），2018（09）.

[6]  华东师大数学系. 数学分析（第4版）[M]. 北京：高等教育出版社，2010.

[7]  王培颖. 浅谈定积分在几何应用中的思想统一性[J]. 数学学习与研究，2011（23）.

[8]  巩小雪. 教学生“学会思考”的思考——从《定积分在物理中的应用》谈起[J]. 数学之友，2015（03）.