基于模糊逻辑评价方法的国际中转集拼中心选址决策
2020-09-26王红艳
王红艳


摘 要:为了研究如何在评价的基础上进行国际中转集拼中心的选址问题,文章结合实际的情况,分析了影响国际中转集拼中心选址的主要因素,建立起了由政治因素、运营因素、成本因素等三个方面的指标因素所组成的综合评价指标体系。并在此基础上,通过运用一种将主观和客观因素有机结合在一起进行评价的模糊逻辑方法,对多个国际中转集拼中心候选地进行多指标评价及排序。最后,通过对一个算例的计算,阐述文中所提出的研究方法的应用步骤及可实施性。
关键词:国际中转集拼中心;综合评价指标体系;语言变量;梯形模糊数
一、国际中转集拼中心选址的综合评价指标的选择
本文结合实际情况,建立一个国际中转集拼中心选址的综合评价指标体系,分别从政治因素、运营因素、成本因素三个大方面进行综合评价,每个方面又建立各自的次一级指标,具体指标因素选取如下:
政治因素中,是否有规范有序的行业法规、开放自由的金融政策、优惠的税收政策、以及该港口在国际航运市场中的地位,这些将会对集拼中心的选址问题产生重大影响。
运营因素方面,港口的泊位数量、航线的数量及覆盖情况是投资者选择的重要因素;同时,稳定且可观的货运量、高效的港口作业效率及可保证的服务品质,也将有利于国际中转集拼中心的选址;此外,货物运抵港口的交通运输是否便利、信息通讯网络是否发达可用、对紧急状况的处理能力是否有保障,也是选址问题所不能忽视的。
成本因素方面,国际中转集拼中心选址地的工程建设费用、设备的购进费用、员工的雇佣费用以及运营期间所产生的各种费用,也是选址问题所必须考虑的,且影响该业务实施的利润水平。
二、基于模糊逻辑评价方法的国际中转集拼中心选址具体实施步骤
1.确定国际中转集拼中心选址的综合评价指标体系
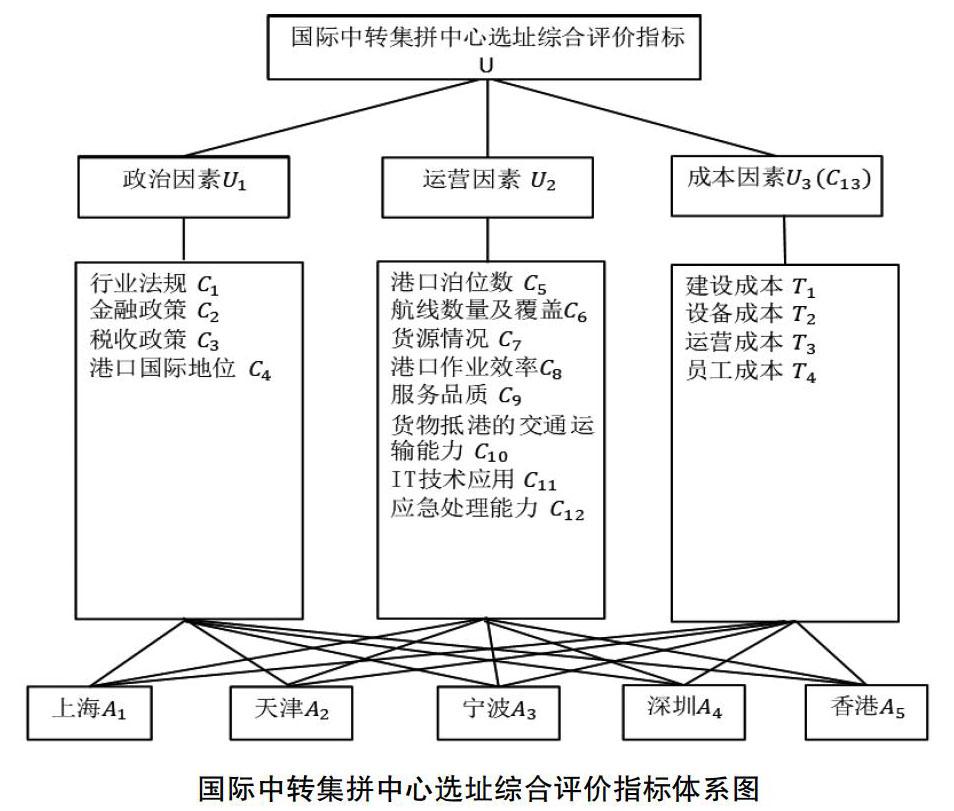
根据实际情况建立国际中转集拼中心选址综合评价指标体系,见下图1。假设因素集U表示评价指标,其中Uh(h=1,2,…,n)表示一级评价指标,Ci(i=1,2,…,n),Tj(j=1,2,…,n)表示二级评价指标,所以将国际中转集拼中心选址问题转化为用因素集U来对候选地址进行综合评价的问题。
2.各评价指标的分类处理
在对实际操作中的指标进行分析时可知,其中大多数为主观因素,而且它们难以用具体的数值进行描述,所以针对这类指标,本文采用梯形模糊数的方法进行无量纲化处理。根据文献,对各因素进行分类,其中Ci(i=1,2,…,n)为主观因素,Tj(j=1,2,…,n)为客观因素,然后采用语言变量值的方法对其进行描述,并将该自然语言变量值进一步用对应的梯形模糊数值进行赋值处理。
3.对专家给出的语言变量数据进行处理
假设邀请了q位专家参与对m个国际中转集拼中心候选地的n种属性通过问卷调查的形式进行评价,下附问卷调查表。则有专家集合D={D1,D2,D3,…,Dq},候选地址集合A={A1,A2,…,Am}。
(1)对于主观因素的处理:
第一步,由每位专家针对上述各主观因素给出基于语言变量的评价矩阵,通过以下计算获得相应的权重向量。他们分别为:
其中,X为各专家的语言变量评价矩阵,w为计算所得的相应的权重向量。
第二步,基于表2中的对应梯形模糊值,对应的梯形模糊数参数根据下面的公式计算所得:
将四个位置上的权重分别求出,得到基于一级语言变量值下不同主观因素所对应的梯形模糊值权重值wi=(ai,bi,ci,di);
第三步,然后根据每位专家给出的针对不同选址地情况下、不同的主观因素的语言变量评价矩阵,对应的参照表3中的梯形模糊值,利用同上述类似的计算方法,分别得到基于二级语言变量值下不同选址、不同主观因素所对应的梯形模糊权重值Smi=(ami,bmi,cmi,dmi)。
(2)对客观因素的处理:
第一步,与此同时也需要对各种客观因素进行无量纲化分析处理,现需要对综合评价指标体系中的n个定量因素,分别对应m个候选地址进行综合评价。对于第j(j=1,2,…,n)个客观因素,在候选地
第二步,结合实际情况,查找各定量因素的相关数据,编制不同候选地所对应的不同定量因素下的四位数字值,分别为dmj、emj、fmj、gmj,然后分别计算每个候选地的综合四位数值tmj。所依据的计算公式如下:
第三步,计算定量因素的相关参数:
第四步,通过下面的公式依次计算相应的梯形模糊适宜指数;
第五步,分别将每个候选地的四位模糊适宜指数相加。
4.结果的比较分析
比较上述过程最终得到的模糊适宜指数,取数值最大者对应的候选地作为最佳的国际中转集拼中心选址地。
三、应用算例
现选定上海、天津、宁波、深圳、香港五地为国际中转集拼中心建设的候选地,邀请4位专家对相关因素指标进行评估,然后通过采用综合评价指标体系对各候选地进行基于模糊逻辑评价方法的综合评价及比较。
1.国际中转集拼中心选址综合评价指标体系的建立
国际中转集拼中心选址综合评价指标体系图
2.对专家给出的语言变量数据进行处理
3.算例分析
通过以上公式的计算,我们得到最终的各个候选地的梯形模糊适宜数,由此可知,四位专家对这五个候选地的偏好顺序依次为:香港2.431,深圳2.157,上海2.042,宁波1.925,天津1.886,所以基于模糊逻辑评价方法的国际中转集拼中心的选址地应为香港最佳。
针对上述数据,我们可以看到香港和深圳凭借得天独厚的地理位置条件、高效的港口作业情况、充沛的集装箱中转货源、完善的税收制度,最终的梯形模糊适宜数较高,是国际中转集拼中心建设的最佳选择。对于国内最先挂牌自贸区的上海,依托国家行业政策的支持、良好的基础设施条件、开放的金融市场,吸引了越来越多的中转货运量,进一步促进了其国际航运中心建设的发展。此外,作为国内第二批挂牌的自贸区城市天津,在国家政策红利与“一带一路”建设的大环境下,天津港有望逐步加强其国际竞争力,吸引更多的中转货物量,为建设国际中转集拼中心奠定更好的基础。
四、结论
本文将已有的相关研究成果与实际情况相结合,建立国际中转集拼中心选址的综合评价指标体系,然后通过将专家所给出的自然语言变量转化为对应的梯形模糊逻辑数值,通过一系列的计算处理,最终得到各个候选地址的梯形模糊适宜数值,从而对各候选地址进行排序,得到最佳的国际中转集拼中心选址地。最后通过一个实际的算例,展现了该方法的实施步骤及可实施性,为相关部门解决国际中转集拼中心选址问题提供了一种可行的方法。
参考文献:
[1]查贵勇.我国发展国际中转集拼业务的思考[J].产业创新研究,2020(11):1-3.
[2]欧阳宇青.”一带一路”倡议下厦门港集装箱国际中转业务拓展研究[J].中国水运(下半月),2019,19(04):45-47.
[3]周一轩.自由貿易港建设背景下天津港向商贸物流港转型升级研究[J].产业创新研究,2018(01):20-24.
[4]丁桂花.上海港国际中转集拼业务创新试点中存在的问题及应对措施[J].水运管理,2016,38(10):17-19.
[6]Dogan Ozgen,Bahadir Gulsum.Combining possibilistic linear programming and fuzzy AHP for solving the multi-objective capacitated multi-facility location problem[J].Information Science,2014(268),185-201.
[7]吴海燕,龙门镖局团队.基于模糊聚类和层次分析法的区域配送中心选址决策应用[J].现代商贸工业,2019,40(12):39-42.
[8]陈磊,刘雪梅,朱文英,陈希昌.基于模糊聚类的物流中心体系选址决策研究[J].物流技术,2014,33(13):247-249+270.
