复杂系统仿真模型可信度评估方法对比
2020-09-26赖宇阳肖开琴方立桥张连怡
赖宇阳 肖开琴 方立桥 张连怡
摘要: 为准确评估复杂系统仿真模型的可信度,以某飞行器非线性动力学模型为研究对象,对比多种传统可信度评估方法和基于复杂性测度的可信度评估方法的准确性。结果表明:传统可信度评估方法可以从单一方面进行模型的可信度评估并得到可信的结果,而基于复杂性测度的可信度评估方法可以综合分析信息熵、复杂度和系统结构认知图等信息,客观定量地评价模型的可信度。基于复杂性测度的可信度评估结果可为其他评估方法的准确性判断提供依据。
关键词: 可信度; 评估; 非线性动力学模型; 复杂性测度
中图分类号: TP391.97 文献标志码: B
Abstract: To accurately evaluate the credibility of complex system simulation model, the nonlinear dynamic model of an aircraft is taken as the research object, and the accuracy of the credibility evaluation methods based on complexity measurement is compared with the traditional ones. The results indicate that the traditional credibility evaluation method can evaluate the credibility of the model from a single way and result in a credible results, and the evaluation method based on complexity measurement can evaluate the model credibility objectively and quantitatively based on the analysis of information entropy, complexity and system structure cognition map. The credibility evaluation results based on complexity measurement can provide basis for accuracy judgment of other credibility evaluation methods.
Key words: credibility; evaluation; nonlinear dynamic model; complexity measurement
0 引 言
仿真技術是科学研究的主要方法之一。仿真系统研究的规模越来越大,技术越来越复杂。模型可信度是复杂系统仿真的关键。目前,模型可信度评估方法有很多种。对于复杂系统,不同模型方法仿真的结果可能存在较大差异。准确评估模型的可信度是复杂系统仿真的基础。因此,研究模型可信度评估方法对复杂系统仿真具有重要意义。
广泛应用的模型可信度评估方法主要有统计学方法、时域分析法、频域分析法和信息学方法等。这些方法主要针对较简单的仿真系统。张淑贵[1]采用假设检验法对2种清洁硅片的工艺系统仿真进行可信度评估。赵善禄等[2]采用时频一致性检验法对武器装备系统的动态数据进行有效性检验。魏华梁等[3]采用灰色关联系数法对导弹系统仿真模型进行可信度评估。罗檬[4]和刘延珍[5]采用TIC法分别评估飞行器仿真模型和导弹系统仿真模型的可信度。王哲等[6]和王博等[7]采用最大熵谱估计法分别对飞机仿真模型和悬架系统仿真模型进行可信度评估。周玉臣[8]采用窗谱分析法评估制导控制仿真系统的侧滑角可信度。
基于复杂性测度理论的模型可信度评估方法是信息学方法的一种,部分学者将其应用于复杂系统仿真模型的可信度评估。[9]赖宇阳等[10-11]基于复杂性测度进行乘员约束系统仿真模型的可信度评估。刘树成等[12]基于复杂性测度评估变矩器流场仿真模型的可信度。
基于上述模型可信度评估方法,本文以某复杂系统动力学仿真模型为研究对象,进行模型可信度评估对比,旨在为复杂系统仿真模型可信度评估提供参考依据。
1 模型可信度评估方法
1.1 常用的模型可信度评估方法
统计学方法采用数理统计进行样本的有效性检验,包括参数估计法和假设检验法。参数估计法利用样本的均值、二阶中心矩和标准误差等参数,通过指定置信度水平划分置信区间,由概率统计得到模型的可信度。假设检验法适用于样本总体服从正态分布的问题。根据统计量的分布类型,假设检验法可分为U检验法(正态分布)、T检验法(T分布)和F检验法(F分布)等。
时域分析法根据样本的时间序列进行数据有效性检验,包括TIC法和灰色关联系数法。TIC法是一种动态性能可信度评估方法,其本质是利用加权原理构造一种误差范数形式。灰色关联系数法主要用于分析数据序列之间的几何接近程度,适用于初值敏感模型的可信度评估问题。
频域分析法主要比较功率谱密度的统计特性是否一致及其一致性程度。根据是否对平稳随机序列求谱,频域分析法可分为窗谱分析法和频响函数置信度准则(freqeuncy response assucance criterion, FRAC)2种方法。窗谱分析法属于非参数化方法,在进行谱估计值的相容性检验之前,直接利用快速傅里叶变换(fast Fourier transform, FFT)对数据序列求谱;在相容性检验阶段,采用类似假设检验的方法构造假设和统计量。窗谱分析法所选窗函数不同,检验结果也不同,常用的窗函数为汉宁窗函数。对于可直接获得功率谱密度的仿真和试验系统,一般采用FRAC方法进行数据的相容性检验。该方法可用于判断所有频响向量在幅值和相位上的一致性,是一种比较严格的模型可信度评估方法。
常用的信息学方法是最大熵谱估计法。该方法是应用最广泛的现代谱估计方法之一,其基本原理是按照系统概率空间熵最大的原则对未知信息进行预测外推,即通过已知信息得到最接近真实系统输出的随机过程。
1.2 系统复杂性测度理论
系统复杂性测度通过对仿真和试验2组原始数据包含的信息熵和变量间的信息结构进行计算和识别,得到仿真数据与试验数据的复杂性、变量之间关联性、系统拓扑结构稳健性等信息,并基于这些信息对模型进行多方面的可信度分析。
系统复杂性测度的计算分为相空间信息分析、整体信息结构认知和复杂性测度等3个部分。
第一部分:相空间信息分析。采用信息熵(香农熵)测度定量计算相空间信息,通过基于互信息测度的广义相关系数定量计算相空间变量之间的非线性相关性。
第二部分:整体信息结构认知。基于Zadeh不相容原理,按照一定的模糊水平分割相空间,将样本点的精确数值转换为等价模糊向量。在此基础上,抽取向量之间的模糊依赖规则,形成系统整体信息结构认知图。
第三部分:复杂性测度。系统的复杂度由系统变量的信息熵、互信息、广义相关性系数等进行描述。
1.3 基于复杂性测度的可信度评估
基于复杂性测度理论对复杂系统仿真模型进行可信度评估,需要依次进行单变量、双变量和多变量分析:首先,对仿真数据和试验数据中的变量逐个进行定量分析比较,完成单变量分析;其次,对相空间形态进行定性分析,对变量之间的相关性进行定量分析,确定变量之间的关联性和耦合度,完成双变量分析;最后,对系统整体信息结构认知图中多变量之间的关系进行定性分析,对复杂性可信度、关联性可信度、稳健性可信度等进行定量分析,三者的加权平均值即为整个系统仿真模型的可信度。
系统复杂性可信度计算公式为ICR=min(Csim,Ctest)max(Csim,Ctest)
(1)式中:Csim为仿真模型的复杂性测度;Ctest为试验系统的复杂性测度。
复杂性测度的计算公式为C=2TENξ
(2)式中:TE为系统信息熵,TE等于所有变量的信息熵之和减去任意两变量间的互信息熵;N为活动节点数;ξ为考虑系统图链接密度的修正因子。
系统关联性可信度计算公式为IRCR=mn
(3)式中:m为2个系统中相同连接度的节点数;n为试验系统图中所有活动节点数。
系统稳健性可信度计算公式为IRBCR=min(Rsim,Rtest)max(Rsim,Rtest)
(4)式中:Rsim为仿真模型的拓扑结构稳健性;Rtest为试验系统的拓扑结构稳健性。
拓扑结构稳健性计算公式为R = (Cr-Cm)2-(Cu-Cm)2Cr-Cm
(5)式中:Cr为系统临界复杂度;Cm为系统最低复杂度;Cu为系统当前复杂度。
2 复杂系统动力学模型可信度评估
以某飞行器动力学模型为研究对象,基于随机振动试验数据,对10~1 000 Hz频率范围内的随机响应分析结果进行可信度评估。试验用振动试验台见图1。
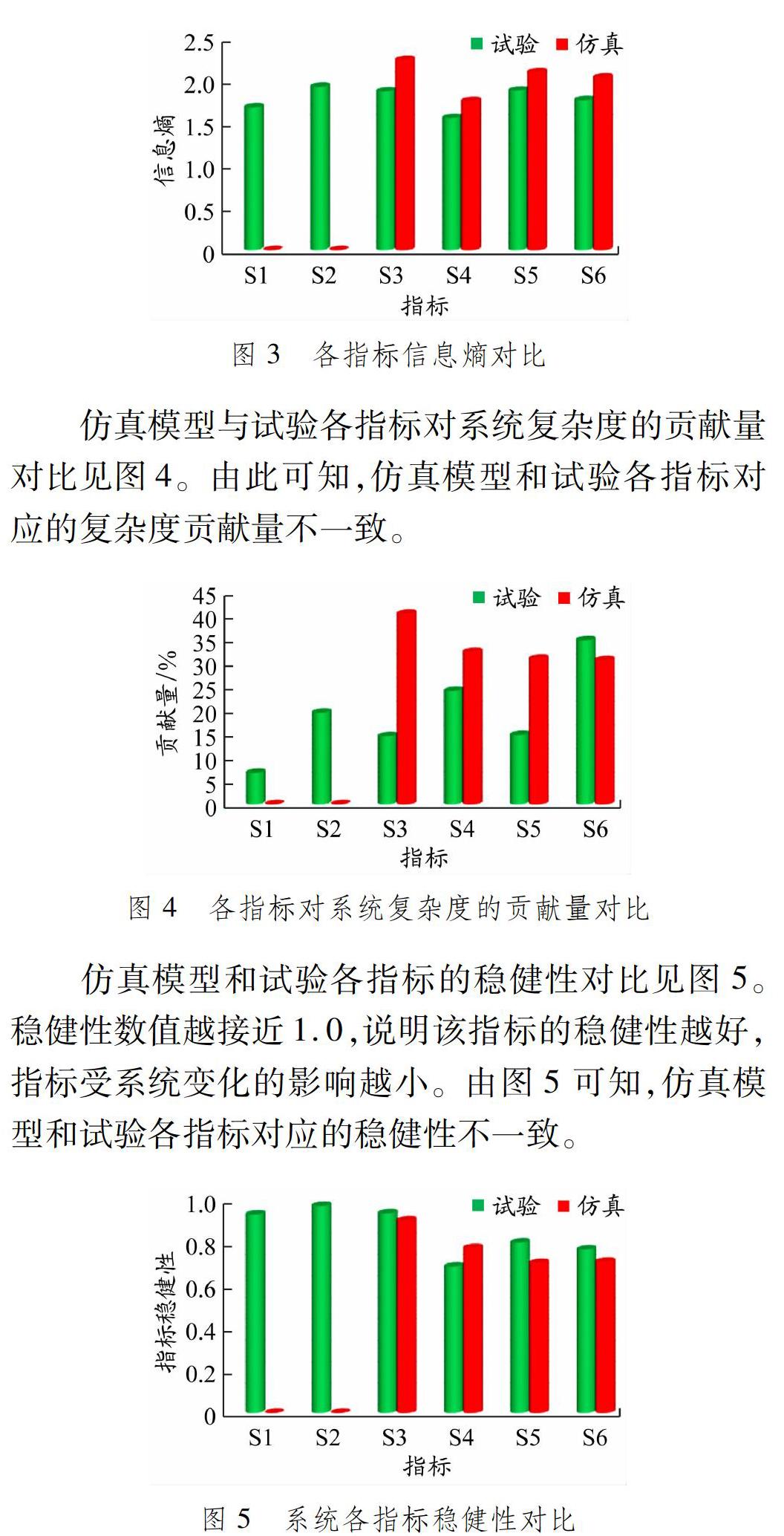
仿真和试验的加速度功率谱密度曲线见图2,其中S1~S6为指标编号,分别对应指标1~指标6。根据统计计算显示,仿真结果的均值和方差分别为33.64 g4/Hz2和0.68 g2/Hz,试验数据的均值和方差分别为22.96 g4/Hz2和0.15 g2/Hz。
2.1 传统可信度评估方法进行模型可信度评估
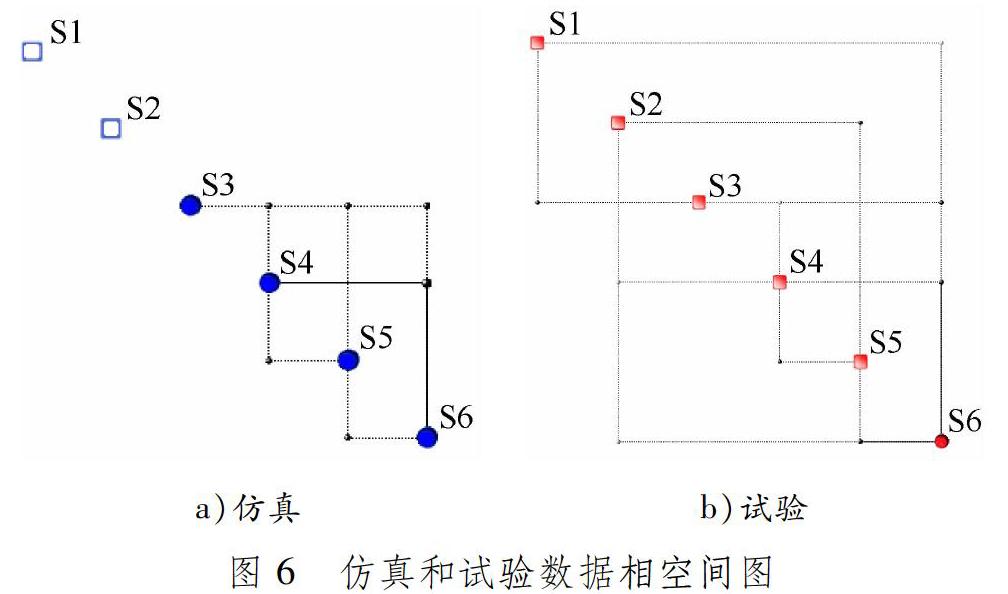
针对该飞行器动力学模型仿真结果和试验数据,采用传统可信度分析算法获得模型可信度评估结果,见表1。
U检验法、T检验法和最大熵谱估计法均依据数据的均值、方差等统计特性进行可信度评估,结合数据的统计特性可知对应算法的可信度得分理应较高。F检验法适用于服从F分布的试验数据,而本文中为正态分布数据,不能获得理想的可信度。窗谱分析法先用FFT对数据进行处理,再进行相容性检验,对于本案例而言属于过度操作,因此无法获得有意义的可信度得分。其他的可信度算法得分参差不齐,在缺乏数据的情况下,无法判断对应方法对本案例模型可信度评估的有效性。
2.2 基于复杂性测度理论进行模型可信度评估
复杂性测度方法可以识别数据的信息结构,得到数据的复杂性、变量之间的关联性和系统图拓扑结构的稳健性等信息,由此可以进行仿真模型复杂性校核可信度评估、关联性校核可信度评估和稳健性校核可信度评估,相应可信度评估结果可辅助案例模型的可信度评估方法选择。
2.2.1 单变量分析
各指标信息熵对比见图3。仿真模型的指标1和指标2信息熵为0,其余指标的信息熵均大于試验模型的信息熵;仿真和试验的系统信息熵分别为19.53和29.43,后者为前者的150.7%,这表示仿真模型不能完全反映试验的不确定性。
仿真模型与试验各指标对系统复杂度的贡献量对比见图4。由此可知,仿真模型和试验各指标对应的复杂度贡献量不一致。
仿真模型和试验各指标的稳健性对比见图5。稳健性数值越接近1.0,说明该指标的稳健性越好,指标受系统变化的影响越小。由图5可知,仿真模型和试验各指标对应的稳健性不一致。
2.2.2 双变量分析
仿真和试验数据的相空间图见图6。图中S1~S6表示指标编号1~6,正交直线相交的节点代表指标间具有广义的相关性。图6中仿真与试验关联节点的拓扑结构一致性较差,且仿真数据对应的总连接数少于试验数据对应的总连接数,说明本案例的仿真模型未能完全反映试验的关联规则。这也可以解释图3中各指标对2个模型复杂度贡献量不一致的问题。
指标3、4、5、6的广义相关性对比分析结果见图7,可见指标之间的非线性程度非常高。试验环境复杂,存在环境噪声或其他不确定因素,导致试验数据的离散性较强、非线性较高;仿真模型存在条件简化且未考虑复杂的环境因素,使仿真环境过于理想,因此所得仿真结果的非线性程度降低。同时,除指标4和指标6以外,仿真数据间的广义相关性均大于试验数据间的广义相关性,说明仿真模型将相应指标之间的关联性进行不必要的强化。
2.2.3 多变量分析
仿真和试验的系统图对比见图8。根据图中的连接密度和活动节点等信息,结合式(2),可计算得到仿真和试验数据的复杂性测度分别为13.81和24.03,后者为前者的1.74倍,说明本案例的仿真模型未能足够反映试验的复杂性。根据式(1)计算得到仿真模型复杂性可信度指标为57.47%。2个系统图中具有相同连接度的节点数为1个,试验系统图中所有活动节点数为6,根据式(3)计算得到仿真模型的关联性可信度指标为16.67%;仿真数据和试验数据的拓扑结构稳健性分别为62.5%和82.8%,根据式(4)计算得到稳健性可信度指标为75.48%。
定义仿真模型复杂性可信度指标、关联性可信度指标和拓扑结构稳健性可信度指标的均值为仿真模型系统复杂性测度的整体可信度指标,用M表示,根据前文数据可以计算得到M=49.87%。
通过仿真和试验数据的复杂性测度可以得到各指标对仿真与试验差距的贡献量,见图9。指标2对仿真与试验数据差距的贡献量最大,为25.84%;指标5的贡献量最小,为10.48%。对应图3中显示的仿真模型与试验模型中各节点的连接度可知,指标2所在节点处仿真数据与试验数据的连接度相差最大,而指标5所在节点处2组数据具有相同的连接度,相差最小。这2处结论可相互印证。
3 结 论
以某飞行器动力学模型为研究对象,基于随机振动测试数据,针对随机响应分析结果,分别采用传统模型可信度评估方法和基于复杂性测度的可信度评估方法,进行仿真模型整体可信度评估,结论如下。
(1)假设检验法和最大熵谱估计法均根据系统的均值和方差,结合相应的分布类型进行模型的可信度评估,在数据统计层面具有较高的可信度,应用于本文研究对象中可以获得较高的可信度得分。这2种方法的缺点是无法进一步表征系统的复杂性相关信息。
(2)窗谱分析法依赖于对数据的FFT,可用于未完成时频变换的系统模型的可信度评估。应用于本文的复杂系统仿真模型时,该方法不能保证可信度评估结果的准确性。
(3)TIC法得到的结果更为严谨,应用于本文复杂系统仿真模型的可信度评估,其得分与基于复杂性测度理论获得的可信度评估分数接近。
(4)复杂性测度理论从仿真模型的复杂性可信度、关联性可信度和稳健性可信度等3个方面全方位评估系统的可信度,可以深度挖掘系统信息。对于本文复杂系统仿真模型的可信度评估,该方法可提供直观可信的评估结果。
(5)复杂性测度理论可全面客观地分析模型的信息,所得可信度结果可以为其他类型模型可信度评估的准确性判断提供依据。
参考文献:
[1] 张淑贵. 假设检验在工程实践中的应用研究[J]. 中国设备工程, 2019(10): 121-122. DOI: 10.3969/j.issn.1671-0711.2019.10.080.
[2] 赵善禄, 李国辉. 基于改进证据理论的时频一致性检验方法研究[J]. 自动化技术与应用, 2019, 38(1): 70-74. DOI: 10.3969/j.issn.1003-7241.2019.01.017.
[3] 魏华梁, 李钟武. 灰色关联分析及其在导弹系统仿真模型验证中的应用[J]. 系统工程与电子技术, 1997(2): 55-61.
[4] 罗檬. 基于数据一致性检验的仿真模型验证方法研究[D]. 哈尔滨: 哈尔滨工业大学, 2017. DOI: 10.7666/d.D01333555.
[5] 刘延珍. 仿真数据智能化分析方法及工具研究[D]. 哈尔滨: 哈尔滨工业大学, 2009. DOI: 10.7666/d.D258907.
[6] 王哲, 李国辉, 赵善禄. 基于最大熵谱估计的某型飞行模拟器动态性能验证[J]. 现代计算机, 2017(34): 3-5. DOI: 10.3969/j.issn.1007-1423.2017.34.001.
[7] 王博, 王明月, 黄朝胜, 等. 基于最大熵谱估计的汽车悬架系统自由衰减振动研究[C]// 2014中国汽车工程学会年会论文集. 上海: 中国汽车工程学会, 2014: 1102-1104.
[8] 周玉臣. 数据一致性分析结果向可信度转换方法及工具研究[D]. 哈尔滨: 哈尔滨工业大学, 2014. DOI: 10.7666/d.D591429.
[9] MARCZYK J, DESHPANDE B. Measuring and tracking complexity in science[C]// Unifying Themes in Complex Systems. Berlin: Springer, 2010: 27-33. DOI: 10.1007/978-3-540-85081-6_4.
[10] 賴宇阳, 方立桥. 基于SV2的汽车乘员约束系统仿真模型可信度验证系统[J]. 计算机辅助工程, 2018, 27(1): 22-27. DOI: 10.13340/j.cae.2018.01.004.
[11] 赖宇阳, 叶芳, MARCZYK J. 基于复杂性测度的乘员约束系统仿真模型可信度验证方法[EB/OL]. [2020-03-09]. http://www.soyotec.com/nd.jsp? id=82.
[12] 刘树成, 魏巍, 闫清东, 等. 基于复杂性测度的变矩器流场仿真模型可信度分析[J]. 农业机械学报, 2012, 43(10): 19-24. DOI: 10.6041/j.issn.1000-1298.2012.10.004.
(编辑 武晓英)
