基于Abaqus和Isight的水下壳体声散射优化

赵晓腾 任春雨

摘要： 针对水下椭圆壳的声散射优化问题，以壳体声散射强度最小为优化目标，以截面特征参数为设计变量建立模型。采用有限元与无限元耦合的混合优化方法，利用Python和Abaqus二次开发求解远场声散射强度，并结合Isight对水下壳体声散射进行优化。根据优化结果改进椭圆壳截面几何参数，可有效降低其声散射强度。

关键词： 椭圆壳; 声散射; 耦合; 优化; 单频; 多频

中图分类号： U674.941; TB115.1   文献标志码： B

Abstract： As to the optimization of acoustic scattering from an underwater elliptical shell， the model is built by taking the minimum scattering intensity of shell as the optimization object， and taking section characteristic parameters as design variables. Python and Abaqus secondary development are used to solve far-field scattering intensity by the hybrid optimization method of the coupling of finite element and infinite element. The acoustic scattering of underwater shell is optimized by combing with Isight. The geometric parameters of elliptical shell section are improved based on the optimization results， and the acoustic scattering intensity is reduced effectively.

Key words： elliptical shell; acoustic scattering; coupling; optimization; single frequency; multi-frequency

0 引 言

水下航行器声隐身设计的重点在于改善结构的声辐射和声散射特性，目前主要利用优化方法达到该目标。近年来，关于结构声辐射优化问题的研究比较活跃。成嘉鹏等[1]利用水下双层圆柱壳结构的声辐射代理模型，实现圆柱壳的结构声学优化设计;ZHENG等[2]优化约束层阻尼贴片的位置、长度和黏弹性层的剪切模量，使简支挡板的辐射声功率最小;ZHAO等[3]对水下壳层结构双材料分布进行拓扑优化，使其声功率级最小;林长刚等[4]利用Isight和ANSYS軟件对SWATH船的支柱体板架结构参数进行声辐射优化，并通过声辐射传递函数计算，对优化后的结构方案进行有效性验证;MERZ等[5]基于梯度优化方法优化潜艇谐振变换器的虚拟刚度、阻尼和质量，使其辐射声功率降到最低;NIU等[6]应用离散材料优化公式实现复合板材纤维角度、堆叠顺序和材料选择的优化，可减小复合板的辐射声功率。在这些研究中，声辐射优化方面的工作较多，声散射优化工作相对较少。陈彤彤[7]采用遗传算法对不同情况下吸声涂层的参数进行优化，得到无界面和存在界面时使平面结构声反射系数最小的聚脲参数选择方式;FEIJO等[8]借助梯度算法对刚体形状进行优化，使刚体散射强度最小;DIVO等[9]采用遗传算法对刚体形状进行优化，使声源处的声学势能最小。分析这些工作可以发现，当前的声散射优化研究还仅限于刚体结构和单频问题，但在实际工程中，多数结构不能视为刚体，因此引用这些结论是不可靠的。为此，有必要开展关于弹性结构的声散射优化研究。

在算法研究方面，已有多种优化算法[10-13]被应用于结构的形状优化研究中，这些算法主要分为局部优化算法和全局优化算法2种。全局优化算法具有良好的全局搜索特性但计算量较大，局部优化算法具有良好的局部搜索特性但不够全面。[14]近年来，混合算法不断被提出并运用于结构优化问题中。PLEVRIS等[15]提出一种基于梯度的拟牛顿序列二次规划方法的粒子群混合优化算法，用于处理结构优化问题，该算法能较好地挖掘设计空间，并能检测出全局最优解的邻域;TAHK等[16]提出一种结合进化算法和梯度搜索技术的混合优化算法，并将其用于连续参数优化问题中。但是，这些混合算法在声学优化问题中使用很少。

针对弹性体声散射几何优化问题中存在的不足，本文以椭圆壳为研究对象，提出一种新的优化分析方法。首先，利用Python对弹性体的声散射分析进行参数化建模;然后，充分利用Abaqus软件强大的有限元和无限元分析能力，将二者耦合完成声目标强度计算分析;最后，基于Isight优化软件，运用混合优化算法完成单频圆柱刚体、多频圆柱刚体和弹性体截面几何参数的优化，使得壳体目标强度最小。

1 理论方法

1.1 有限元和无限元耦合声散射分析

Abaqus软件具有较强的声学分析能力。成嘉鹏等[1]利用Abaqus完成无限流域中双层圆柱壳声固耦合的一体化分析。吴健等[17-18]将Abaqus的有限元与无限元相结合，准确、有效地求解水下结构声辐射问题。基于前人的研究，本文将Abaqus的有限元与无限元相耦合，求解无限流域内结构的声散射问题。

选取平面波作用下弹性球壳在无限流域中的声散射问题为校验算例。水中弹性球壳外径a=1 m，内径b=0.9a，入射波为幅值1 Pa的平面波。球壳材料密度ρ=7 700 kg/m3，弹性模量E=2×1011 Pa，泊松比v=0.3;水的密度ρ=1 000 kg/m3，水中声速取c=1 500 m/s;计算背向距离R=1 000 m处的散射声压。

弹性球壳局部有限元网格模型见图1。内部（黄色）区域为有限元声场，网格划分时定义为声学单元;中间（橙色）区域划分为结构网格;外层（绿色）区域为有限元声场，网格划分时定义为声学单元。外部边界通过Skin定义为无限元边界，同时赋予其“声学无限元”属性，网格划分时将其定义为声学无限元单元。结构与内部水域接触面、结构与外部水域接触面通过Tie绑定约束，使水体与结构表面始终保持接触而不分离。此外，通过关键字Incident wave完成内部水域表面、结构内外表面和外部水域内表面相互作用设置，入射波设置为平面波。

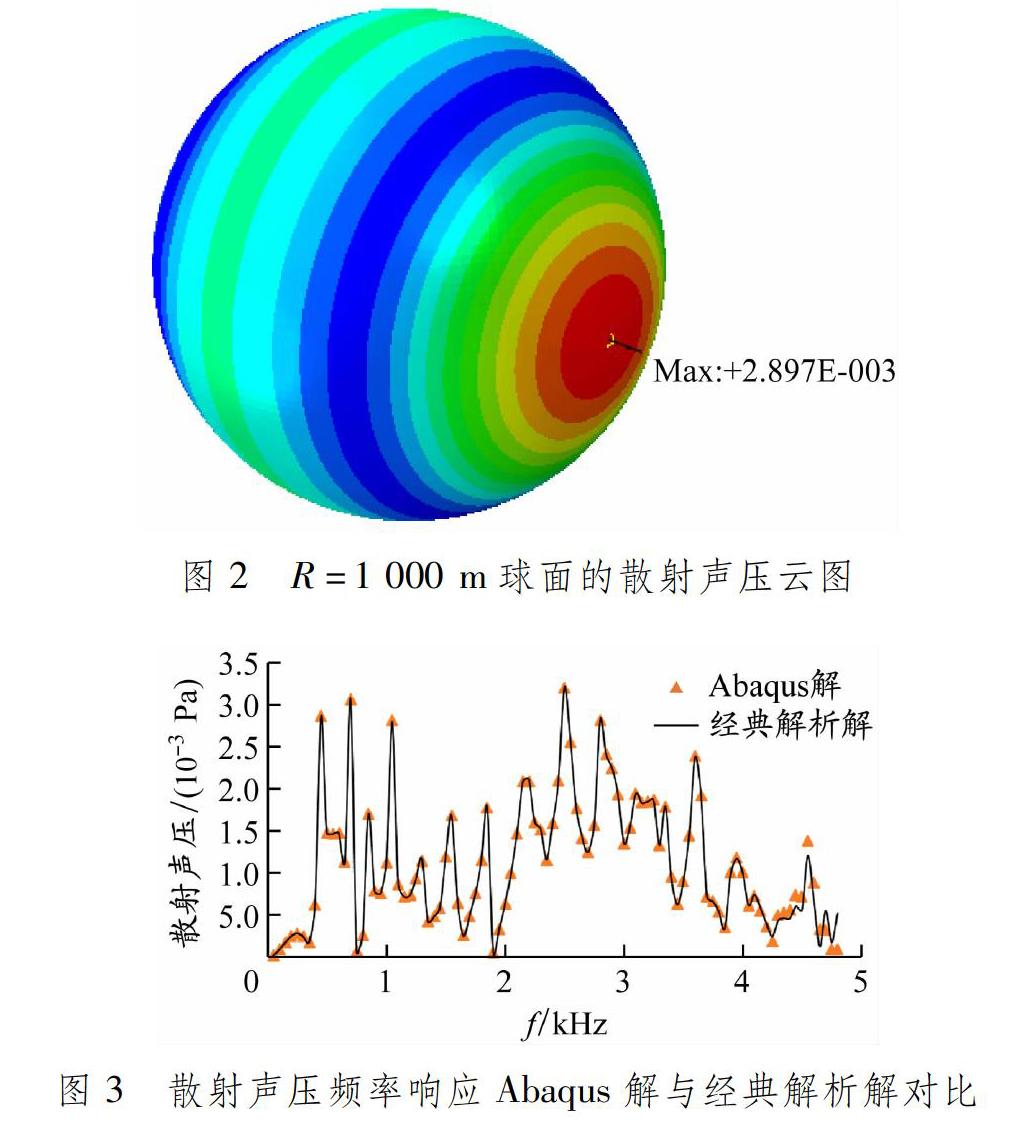
通过有限元与无限元的耦合处理，可求得声学无限单元表面的散射声压值。任意远处的散射声压分析通过远场分析插件Acoustic Visualization完成。当入射波为450 Hz时，R=1 000 m球面的散射声压云图见图2，此时背向散射声压最大。散射声压频率响应Abaqus解与经典解析解对比见图3，其中三角形标注的离散点为本文Abaqus软件仿真结果，曲线为文献[19]的经典解析解。由此不难看出，本文将有限元与无限元耦合的方法能准确求解弹性体的目标强度。

1.2 优化方法

传统优化设计采用试算法，即凭借经验进行优化，因此效果往往缺乏创新性。为弥补传统优化的不足，借助Isight优化软件提出一种新的优化思路。首先，利用Python将Abaqus求解结构声散射问题代码化，形成相应的py文件，其中包括结构参数化建模、赋予属性、划分网格，以及添加约束和相互作用等;然后，将py文件、Abaqus的bat批处理文件和dat结果文件输入Isight优化软件;最后，采用混合优化算法完成椭圆壳形状的自动分析和优化迭代，获得目标强度最小的形状方案。

混合优化算法是全局优化算法和局部优化算法的混合运用，具体就是先利用全局优化算法快速缩小最优解范围，再利用局部优化算法快速准确确定最优解。混合算法能避免单一算法收敛性较差（全局优化算法）或局部收敛（局部优化算法）的弊端。以混合优化算法为依据的截面几何结构优化流程见图4。在Isight中实现混合优化算法，其中：全局优化算法选择多岛遗传算法，子群大小为5，进化代数为5，交叉率为0.7，变异率为0.01;初始种群为参数的初始集合x，评价函数为优化数学模型的目标函数最小，其中目标函数中的声目标强度由Abaqus的有限元与无限元耦合分析得到;经过迁移、交叉、变异和选择等操作，求得使目标强度最小的全局最优解集合x*。局部优化算法选择梯度优化算法中的序列二次规则法，该算法收敛快，适用性较强[20]。最大迭代步数设置为10，相对步长为0.001，此时初始种群变为集合x*，评价函数与多岛遗传算法相同，当目标强度收敛至最小时求得局部最优解集x* *，x* *即为使目标强度最小的截面I和II的几何参数。

2 声散射优化分析

2.1 研究对象

选取椭圆壳为研究对象，椭圆壳声散射模型见图5。壳体总长为2.25 m，初始半径为0.25 m，厚度为0.01 m，密度为3 000 kg/m3，弹性模量为16 GPa，泊松比为0.3。壳体内部为真空，外部由椭球水域包裹，其长轴为1.20 m，短轴为0.70 m，水的密度为1 000 kg/m3，水中声速为c=1 500 m/s。在有限元模型中，有限元网格设置为四边形结构单元，共1 120个;水域网格为六面体单元，其中包括28 224个声学有限单元和4 704个声学无限单元。

2.2 单频和多频优化模型

以图5中截面I和II椭圆特征参数a1、b1、a2和b2为设计变量，且变量在取值范围内取离散值，取值间隔为0.01 m。通过调整椭圆壳的几何外形，降低散射体的背向声目标强度。

2.3 刚体和弹性体模型优化结果

为对比分析，将目标体视为刚体进行优化分析，得到刚性椭圆壳的优化结果。因为不规则目标声散射通常与声波入射方向存在密切关系，所以分别考虑平面波沿轴向入射和正横入射时的情况，给出典型的优化进程。刚性体椭圆壳声波正横入射混合优化进程见图6，图中曲线斜率代表优化速率，其他分析工况与此类似。

由此可见，梯度优化算法优化进程速率比遗传优化算法优化进程速率大，说明在全局优化得到较优解的基础上进行局部优化能快速准确得到最优解，而且收敛性较好。另一方面，虽然全局优化速率相对较小，但是前期全局优化算法的使用可以很好地避免优化陷入局部解，综合来看，混合优化算法能快速准确地解决该声散射优化问题。

声波频率为200 Hz时，弹性椭圆壳和刚体椭圆壳截面参数优化结果对比见表1。在声波轴向入射时刚体和弹性体优化趋势一致，但在正横入射时二者存在较大差异。轴向球冠方向入射可近似为球冠散射，在优化频段[200， 2 000] Hz和目标尺度范围（均值为0.25 m）内，ka（k为优化曲线斜率，a为球冠半径，此时a近似取0.25 m）为[0.2，2.0]。对于刚性体，目标散射仍在低频瑞利区（0

单频优化结果表明，弹性效应会影响弹性体的优化结果，特别是在正横入射情况下。因此，进一步利用多频优化模型开展弹性体声散射优化分析。为验证多频优化方案的可行性，先给出平面波正横入射时刚体优化的情况，优化前、后声散射强度的变化情况见图7。图7中[50， 450] Hz频带内的目标强度略增大，但[450， 2 000] Hz频带内的目标强度得到大幅降低，从整个频段来看，目标强度得到显著降低，这表明本文多频优化方案能有效改善目标散射在多频率点的优化问题。

在弹性体多频优化中，同样考虑平面波沿轴向和正横入射时的情况，截面参数优化结果见表3。由此可以看出，在弹性体轴向入射和正横入射时，二者的优化趋势存在一定差异。平面波轴向球冠方向入射可近似为球冠散射，正横入射可近似为椭圆柱面散射，而且后者还需要考虑谐振，导致二者存在一定差异。

为了解单频和多频优化效果，在弹性体正横入射情况下对比多频优化结果与200 Hz单频优化结果，二者存在较大差异。在此基础上，分别对200 Hz单频优化结果、多频优化结果和原始模型截面形式等3种结构进行声散射强度频率响应分析，声散射强度频谱见图8。由此可知：在200 Hz时单频优化后的声散射强度小于多频优化，但从整体频段上看，单频优化后的椭圆壳声散射强度在讨论频带内未能得到明显改善，而多频优化后的声散射强度比原始模型声散射强度显著降低。由此说明，在单频率点优化上，单频优化结果比多频优化结果更好，但对整体频段优化時，多频优化比单频优化更合适。

3 结 论

基于有限元与无限元耦合的混合优化算法，利用Abaqus和Isight对弹性椭圆壳和刚性椭圆壳进行声散射优化分析，得到以下结论：

（1）采用有限元与无限元耦合的混合优化方法、利用Abaqus软件分析弹性体声散射，可以为这类结构的声学处理提供新的思路和途径。

（2）对于多频声学优化，通过将采样频率点子目标函数加权求和，可获得最终目标函数的优化方向。

（3）在椭圆壳截面几何结构参数优化问题中，刚体和弹性体的优化结果和优化频段与平面波入射方向有关。

（4）同尺度下弹性体与刚体截面几何参数的优化结果具有差异性，优化结果可作为当前声散射优化问题的有效补充。

本文给出的优化思路和分析方法还可用于更广泛的结构声学优化分析中，包括壳体内部结构优化（例如壳体内部肋骨和平台）和柱壳外附体结构优化（例如水下航行器的舵和围壳）等。

参考文献：

[1] 成嘉鹏， 杨德庆， 易桂莲. 水下圆柱壳声学代理模型优化设计[J]. 噪声与振动控制， 2016， 36（3）： 1-5. DOI： 10.3969/j.issn.1006-1335.2016.03.001.

[2] ZHENG H， CAI C. Minimization of sound radiation from baffled beams through optimization of partial constrained layer damping treatment[J]. Applied Acoustics， 2004， 65（5）： 501-520. DOI： 10.1016/j.apacoust.2003.11.008.

[3] ZHAO W C， ZHENG C J， LIU C. Minimization of sound radiation in fully coupled structural-acoustic systems using FEM-BEM based topology optimization[J]. Structural and Multidisciplinary Optimization， 2018， 58（1）： 115-128. DOI： 10.1007/s00158-017-1881-3.

[4] 林长刚， 孙建刚， 余越， 等. 船舶加筋板架结构低噪声优化研究[J]. 舰船科学技术， 2019， 41（3）： 24-30. DOI： 10.3404/j.issn.1672-7649.2019.03.005.

[5] MERZ S， KESSISSOGLOU N， KINNS R， et al. Minimisation of sound power radiated by a submarine through optimisation of its resonance changer[J]. Journal of Sound and Vibration， 2010， 329（8）： 980-993. DOI： 10.1016/j.jsv.2009.10.019.

[6] NIU B， OLHOFF N， LUND E， et al. Discrete material optimization of vibrating laminated composite plates for minimum sound radiation[J]. International Journal of Solids and Structures， 2010， 47（16）： 2097-2114. DOI： 10.1016/j.ijsolstr.2010.04.008.

[7] 陈彤彤. 基于某材料的水下声隐身研究[D]. 哈尔滨： 哈尔滨工程大学， 2011. DOI： 10.7666/d.y2053066.

[8] FEIJO G R， OBERAI A A， PINSKY P M. An application of shape optimization in solution of inverse acoustic scattering problems[J]. Inverse Problems， 2004， 20（1）： 199-228. DOI： 10.1088/0266-5611/20/1/012.

[9] DIVO E A， KASSAB A J， INGBER M S. Shape optimization of acoustic scattering bodies[J]. Engineering Analysis with Boundary Elements， 2003， 27（7）： 695-703. DOI： 10.1016/s0955-7997（03）00022-5.

[10] FOURIE P C， GROENWOLD A A. Particle swarm optimization algorithm in size and shape optimization[J]. Structural and Multidisciplinary Optimization， 2002， 23（4）： 259-267. DOI： 10.1007/s00158-002-0188-0.

[11] BELEGUNDU A D， SALAGAME R R， KOOPMANN G H. A general optimization strategy for sound power minimization[J]. Structural Optimization， 1994， 8（2/3）： 113-119. DOI： 10.1007/BF01743306.

[12] TANG X G， BASSIR D H， ZHANG W H. Shape， sizing optimization and material selection based on mixed variables and genetic algorithm[J]. Optimization and Engineering， 2011， 12（1/2）： 111-128. DOI： 10.1007/s11081-010-9125-z.

[13] HASHIMOTO H， KIM M G， ABE K， et al. A level set-based shape optimization method for periodic sound barriers composed of elastic scatterers[J]. Journal of Sound and Vibration， 2013， 332（21）： 5283-5301. DOI： 10.1016/j.jsv.2013.05.027.

[14] GUDLA P K， GANGULI R. An automated hybrid genetic-conjugate gradient algorithm for multimodal optimization problems[J]. Applied Mathematics and Computation， 2005， 167（2）： 1457-1474. DOI： 10.1016/j.amc.2004.08.026.

[15] PLEVRIS V， PAPADRAKAKIS M. A hybrid particle swarm-gradient algorithm for global structural optimization[J]. Computer-Aided Civil and Infrastructure Engineering， 2011， 26（1）： 48-68. DOI： 10.1111/j.1467-8667.2010.00664.x.

[16] TAHK M J， WOO H W， PARK M S. A hybrid optimization method of evolutionary and gradient search[J]. Engineering Optimization， 2007， 39（1）： 87-104. DOI： 10.1080/03052150600957314.

[17] 吳健， 李泽成， 熊晨熙. 基于Abaqus的水下结构声辐射仿真方法[J]. 计算机辅助工程， 2015， 24（6）： 37-41. DOI： 10.13340/j.cae.2015.06.007.

[18] 吴健， 何涛， 王纬波. 基于Abaqus 的舷间充水双层壳体水下声辐射计算方法验证[J]. 中国造船， 2019， 60（1）： 175-184. DOI： 10.3969/j.issn.1000-4882.2019.01.017.

[19] HICKLING R. Analysis of echoes from a hollow metallic sphere in water[J]. Journal of Acoustical Society of America， 1964， 36（6）： 1124-1137. DOI： 10.1121/1.1919173.

[20] 吴加同， 石敏， 任春雨. 复合材料舵固有频率优化设计[J]. 中国舰船研究， 2018， 13（2）： 84-90. DOI： 10.3969/j.issn.1673-3185.2018.02.011.

[21] 饶玉成. 基于参数自适应的极大熵结构优化算法研究[D]. 北京： 北京工业大学， 2003： 10-11.

[22] 罗海林. 离散变量结构拓扑优化的遗传禁忌搜索算法研究[D]. 北京： 北京工业大学， 2006： 7-8.

（编辑 武晓英）