新高次四维超混沌系统的广义反同步*

郑 莉，孙常春

(沈阳建筑大学 理学院，沈阳 110168)

近十年来，混沌理论[1]得到了迅速发展.混沌系统的特殊性在于加入了确定性输入后，产生了类似随机的运动，即内随机性.这种内随机性不同于一般随机性，也不同于周期性，具有两种特点.经大量研究发现，混沌广泛存在于人类研究的各个领域.混沌现象不仅在流体力学、物理学、化学等领域被研究和应用，医学上已经证实，麻疹的流行、血细胞生成、心肺功能的相互作用等多种人体生物现象也都是呈混沌态的.同时在社会科学中，混沌理论也被用来探讨人口迁移和用电预测[2]等社会现象.已有学者提出，将混沌信号应用在人工智能中，人类将得到更高智慧的人工智能.目前对混沌理论的研究包括：提出特殊的新系统，如没有平衡点的系统[3]、多平衡点的系统[4]、具有无穷多平衡点的系统[5]、具有共存吸引子的系统[6]、高维系统[7]、高次系统、分数阶系统[8]、切换系统[9]或者兼具以上特征的多特征系统.对这些系统进行动力学分析，证明其混沌性，挖掘其新的特征并进行同步分析[10]和电路实现[11].在以往所提出的高次混沌系统中，含6次项的高次系统已经较为特殊，本文提出了含13次项的四维超混沌系统，其在x1-x2-x3三维空间中呈帽子形，在x1-x2平面投影为嘴唇形.

1 四维超混沌系统

1.1 超混沌系统概述

四维超混沌系统的表达式为

(1)

式中，a、b、c、d、e、f、g、h、l、m、n为系统中的未知参数.式(1)中包含了11项，其中5个1次项，3个2次项，1个3次项，1个6次项，1个13次项.

1.2 超混沌系统的相图及李雅普诺夫指数谱

当a=20，b=14，c=4，d=8，e=6，f=5，g=11，h=2.8，l=1.5，m=1，n=1且初始值取(0.01，0.01，0.01，0.01)时，系统(1)是混沌的，其相图如图1所示.

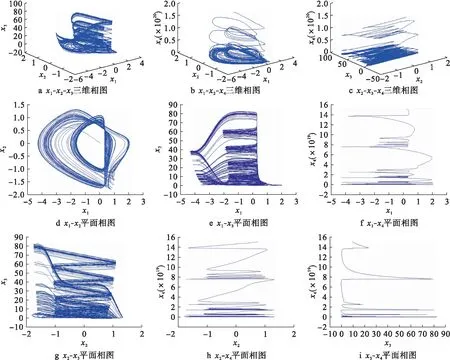
图1 系统(1)相图

选取初始值为(0.01，0.01，0.01，0.01)时，系统(1)在1 000 s以内的Lyapunov指数谱如图2所示.

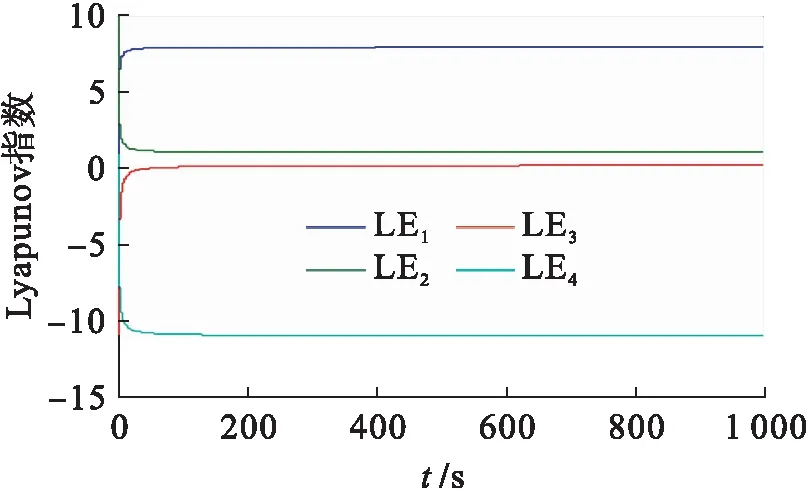
图2 系统(1)Lyapunov指数谱

式(1)状态方程的维数为4，状态方程的阶数大于2，且LE1>0，LE2>0，LE3=0，LE4<0，LE1+LE2+LE4<0，故系统(1)为超混沌系统.

2 广义反同步控制器设计及仿真实验

2.1 非线性广义反同步控制器设计

响应系统和驱动系统的轨道之间满足某一特定函数关系的同步，称为广义同步，本文给出设计非线性广义反同步控制器的方法.指定系统(1)为驱动系统，则响应系统为

(2)

令

(3)

将式(2)与式(1)相加，可得

(4)

令非线性控制器为

(5)

将式(5)代入式(4)，则有

(6)

e1(-ae2+ω1)+e2(de2+ω2)+

e3(-ge3+ω3)+e4(me1+ne4+ω4)

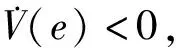
(7)

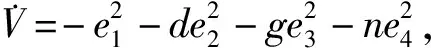
2.2 仿真实验

在Matlab平台下，取误差为10-6，x1(0)=0.01，x2(0)=0.01，x3(0)=0.01，x4(0)=0.01，y1(0)=0.02，y2(0)=0.02，y3(0)=0.02，y4(0)=0.02，在非线性控制器作用下，驱动系统与响应系统能迅速同步.图3为加入控制器时系统(1)和(2)的反同步误差曲线.

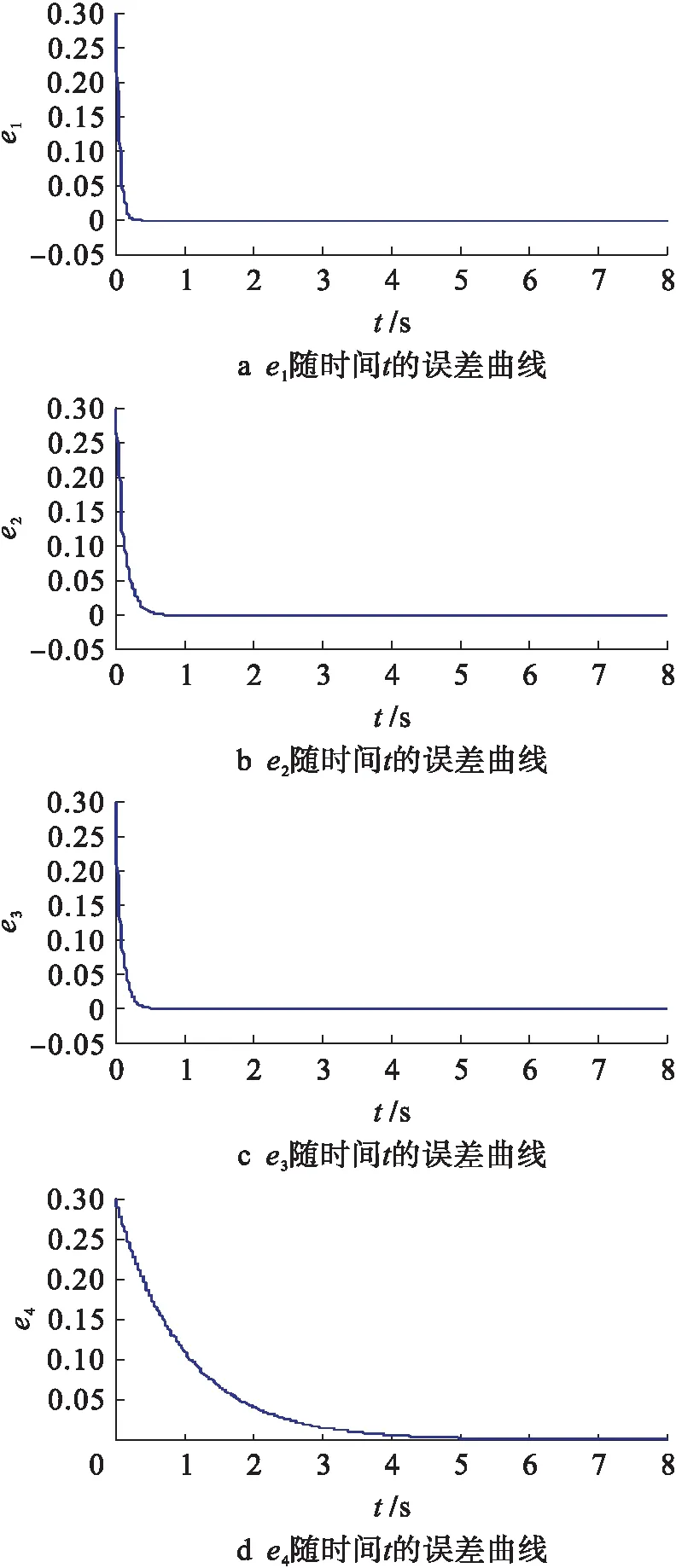
图3 加入控制器时系统(1)和(2)的反同步误差曲线

3 结 论

本文提出了含超高次项四维超混沌系统，在非线性反同步控制器作用下，驱动系统与响应系统能够迅速同步.因该超混沌系统具有一定的特殊性，在保密通信及图像加密中具有更高的实用价值.