神经网络梯度下降与粒子群组合的训练算法

郭松林， 王朝晖

(黑龙江科技大学 电气与控制工程学院， 哈尔滨 150022)

0 引 言

神经网络是当今人工智能研究的主流内容,在深度学习领域具有很强的潜力[1]。神经网络在迭代过程中主要采用的是梯度下降算法，随着科技的进步，梯度下降算法已经有诸多优秀的算法，如SGD、SGDM、CM、Adagrad和Adam等。

Adam算法是现今使用最多的深度学习算法，该算法容易跳过鞍点，能够自适应调节学习率。但是梯度下降算法会导致代价函数陷入局部最小，造成收敛慢或不收敛的情况。对梯度下降算法的优化[2]，采用遗传算法[3]、退火算法[4]、粒子群算法[5-6]等算法进行改进,均取得了有效的进展，但是，大多优化是对网络连接结构、网络初始值的优化，并未从根本上改善迭代中发生的局部最小问题。

笔者基于梯度下降算法，将粒子群算法与之组合构成新算法，其结合了粒子群算法不易陷入局部最小和Adam较强寻优的特点，以使模型收敛更快，精度更高。

1 神经网络

1.1 网络结构

神经网络包括输入层、隐含层、输出层。文中的网络模型采用多输入多输出结构，拓扑结构如图1所示，其中，x1，x2，…，x4为网络输入，b1，b2，…，b4为各神经元偏置，y1，y1，y3为网络输出。

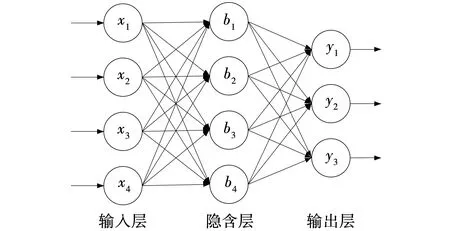
图1 网络拓扑结构Fig. 1 Network topology structure

式中，wij——隐含层权重，i=1，2，…，4，j=1，2，…，4。

通过隐含层的线性变换后，需要引入非线性激活函数g(θ),得到最终隐含层输出函数为

隐含层到输出层的映射关系为

与前一层的局部接受域相连，输出层表示某一输入数据的分类情况，即属于各个类别的数值大小。

1.2 非线性激活函数

在现代神经网络架构中，激活函数多种多样，目的均是为了将线性映射变为非线性映射，用来增强模型的拟合能力，常见的非线性激活函数是ReLU和Logistic表达式为

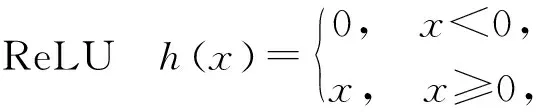
文中采用的非线性激活函数是ReLU，相比之下，梯度容易求解，运算速度快。而且神经网络在进行参数训练时，由于链式法则，偏导数在反向传播过程中绝对值会越来越小，几乎为0。如果采用Logistic激活函数，当输入绝对值很大的话会出现“饱和”的情况，即倒数趋近于0，而ReLU不会饱和，在激活的时候导数恒定为1，可以避免“梯度消失”。

1.3 softmax分类

softmax函数，也称归一化指数函数，目的是将有限项离散分布的数据进行对数归一化，使多分类的结果以概率值的形式展现出来。文中将softmax用于多分类任务中，将神经网络输出的多个数值映射到(0,1)区间内。

在n分类任务中，样本x属于第j个分类的概率为

(1)

由式(1)可知，指数函数的值域是非负数，将神经网络的结果映射到指数函数上，可以保证概率的非负性。各种预测结果的概率之和为1。

1.4 交叉熵损失

交叉熵是信息论中的一个概念，主要用于计算两类数据之间的差异性大小。在神经网络中，希望训练数据在模型上得到的数据值与真实数据值越接近越好，而这种数据间的差异性可以由交叉熵损失值表现出来，因此，文中选用交叉熵作为损失函数，用来度量真实值和预测值之间距离。

损失函数为

式中：y——期望输出,即有监督训练的标签；

o——实际输出,即经过模型运算给出的结果；

N——训练的总样本数。

2 BP-PSO组合算法

2.1 梯度下降算法

Adam是如今深度学习中使用最为广泛的一种随机梯度下降算法，它最大的特点是可以自适应调节学习率，对参数的每个分量使用不同的学习率进行更新，打破了所有参数使用同一学习率进行迭代的束缚。待训练参数的不同分量使用不同的学习率进行更新，可以减少震荡，提高收敛效果，进而识别出那些非常具有价值但易被忽略的微小特征。

Adam算法是基于动量法的一种拓扑。它在一阶矩估计的基础上加入了二阶矩估计[8]，计算公式为

mt=β1mt-1+(1-β1)gt，

式中：mt、ut——gt一阶矩和二阶矩的估计量；

β1、β2——衰减常数，β1、β2∈[0,1)。

对mt和ut的偏差修正为

Adam的参数更新公式为

式中：θ——待训练参数值,即网络中权重和偏置；

α——初始学习率；

ε——很小的正数，为了避免分母为0的情况，一般取10-8。

对于自适应学习率算法的性能问题，有关学者使用CIFAR-10数据集，对SGD、CM、Adagrad以及Adam 的实际性能进行比较，结果表明，Adam算法在测试集与训练集中的优化效率都是最高的。

2.2 粒子群算法

粒子群算法(PSO)是通过对飞鸟群觅食行为的研究总结得来，1995年，Eberhart和Kennedy提出PSO算法。这种通过研究某一物种行为特性的算法在求解优化问题中被广泛使用，它的主要特点是，单个生物的动作与行为往往比较单一，但是当站在整个生物种群的角度时，会发现往往会取得意想不到的结果。这与计算机单一且运算能力庞大的特性十分吻合。

粒子群算法拥有良好的全局寻优能力[7]，其利用一种粒子来模拟每一只鸟类个体，粒子群中的每一个粒子都表示处于解空间中的一个潜在的解，每个粒子所处的位置即为待优化问题的一个候选解，粒子的飞行过程即为个体的寻优过程。根据粒子的最优位置和种群的最优位置对粒子的速度进行实时调整，粒子的速度代表每次迭代粒子移动的快慢。

个体极值是每一个粒子单独搜寻得到的最优解，全局最优解是粒子群中最优的个体极值。每次迭代，更新每个粒子速度和位置，达到终止条件后得到全局最优解。

算法包括初始化，个体极值与全局最优解，更新速度和位置的公式，终止条件。

(1)初始化。迭代开始前，要对粒子群算法的超参数进行设置，包括最大迭代次数、粒子群中粒子的个数、粒子的初始位置和初始速度，整个搜索空间的范围。

(2)个体极值与全局最优解。定义适应度函数，用于求解每个粒子的极值，个体极值为每个粒子在适应度函数上找到的最优解，从这些所有粒子的最优解中对比寻找全局极值，该数值所对应的粒子为全局最优解。每次迭代完成后，需要更新个体极值与全局最优解。

(3)更新速度和位置的公式。在d维解空间中，第i个粒子的坐标位置为xi=(xi1,xi2,…,xid)，其移动速度为vi=(vi1,vi2,…,vid)，每个粒子当前极值为pi=(pi1,pi2,…,pid)，该种群当前的全局极值为pg=(pg1,pg2,…，pgd)，下一次迭代时粒子的位置和速度为

xi+1=xi+vi，

vi+1=wvi+c1R1(pi-xi)+c2R2(pg-xi),

式中：w——惯性权值；

c1、c2——加速因子；

R1、R2——均匀分布于[0,1]的随机数，且相互独立。

(4)终止条件。在达到设定的迭代次数或相邻迭代之间的差值满足最小界限时，迭代终止。此时选择粒子群中全局最优解对应的粒子作为最优解。

2.3 BP与PSO的组合算法

组合算法流程如图2所示。

图2 组合算法流程Fig. 2 Combined algorithm flow

首先，随机初始各个神经元的权重w和偏置b，并且确定粒子群算法中的粒子个数n和展开粒子群算法的空间大小。然后，将训练数据随机排序，输入神经网络开始进行梯度下降训练，可得经过训练后的各神经元的权值和偏置，由式(2)可计算当前损失函数大小。循环训练40步后，将更新后权值w和偏置b看作解向量代入式(3)，在梯度下降解的基础上用PSO算法进行60次寻优，这里寻优的解空间是以原解为中心，空间拓扑出来的一个邻域，该邻域的大小是算法新引入的一个超参数，与学习率类似，最后将PSO得到的最优粒子(即神经元的权重与偏置)重新代入梯度下降算法，以100步为周期进行下一次循环训练。

3 实验与结果分析

3.1 实验环境及配置

实验在Window10，64位操作系统上搭建Tensorflow作为深度学习框架，软件编程基于Python3.7.7的深度学习函数库，内置了深度学习和计算机视觉方面的很多通用算法。用来训练的CPU和GPU型号分别为Intel i5-7300HQ和Nvidia GTX1050。

实验共有数据150组，部分数据见表1，每组包括四个特征参数(花萼长、花萼宽、花瓣长、花瓣宽)以及与该特征向量对应的鸢尾花类别。类别分为三类，包括狗尾草鸢尾、杂色鸢尾、弗吉尼亚鸢尾，分别用数字0、1、2表示。

表1 鸢尾花数据集Table 1 Iris data set

每次训练之前，需将150组数据的顺序随机打乱，分割为训练集和测试集，其中，训练集为前120组，测试集为后30组。

3.2 模型训练过程

设定初始学习率lr为0.001，粒子群解空间space为0.01，迭代次数n为500，批batch大小为30，将120组数据分为4批进行训练，将每个批次计算出的损失值Loss累加求均值，这样计算的Loss更准确。

分别创建BP网络模型和BP-PSO网络模型，将两种方法作比较。开始训练网络，利用算法最小化交叉熵损失Loss，优化网络连接权值。每次训练完成后保存参数，将测试集数据输入模型中进行测试。

3.3 结果分析

训练过程中的交叉熵损失Loss以及模型准确率σ变化过程分别如图3、4所示。

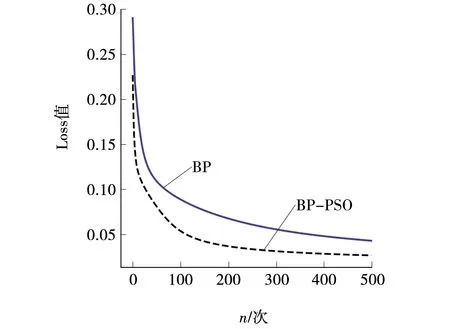
图3 交叉熵损失Fig. 3 Cross entropy loss

图4 模型准确率Fig. 4 Model accuracy

通过对比损失函数Loss可以看到，BP-PSO算法收敛的速度更快一些，在训练达到500步左右，BP-PSO算法Loss值就趋于稳定，损失值为0.024 93，而BP算法损失值为0.050 3，Loss值仍然处于较高值。组合算法损失值下降了49.54%，明显优于梯度下降算法。

模型准确率是在30组测试集数据上统计的平均值，BP算法在达到300步之后将准确率稳定到100%，而BP-PSO算法在迭代131步之后达到稳定，收敛速度提高了43.33%。

4 结束语

针对梯度下降算法容易出现的局部最小问题，提出了梯度下降法(BP)和粒子群算法(PSO)结合的组合训练算法，对神经网络中各神经元的权重和偏置进行寻优计算。通过实验研究表明，该组合算法可以达到更高的精度和更快的收敛速度。但是，由于该方法在原始梯度下降中引入了粒子群算法，导致网络模型中加入了额外的的超参数，如粒子群数量和收索空间的大小等，使调参问题变得更加复杂，这将成为作者今后改进和研究的方向。