图像特征匹配环境下SIFT算法的改进

程俊廷， 张俊峰， 胡 瑾

(1.黑龙江科技大学 机械工程学院， 哈尔滨 150022； 2.合肥财经职业技术学院 人工智能学院， 合肥 230000)

0 引 言

在建筑物三维重建的过程中，对采集的图像进行特征匹配，是至关重要的一个环节[1]。图像特征匹配既可以利用相对较少的图像比如两幅，也可以用更多的图像，比如三幅乃至更多，通过特定算法，对图像内容、关系、结构等进行相似性和一致性分析，从而识别出同名点的过程。特征点的匹配分为三个步骤：第一步为特征提取，第二步为特征描述，最后一步为特征匹配。特征提取就是从给定的图像中提取出关键点(或角点、特征点)等[2]。特征描述就是利用数学向量对提取到的关键点进行一系列的描述，其目的是为了保证向量和特征点之间一一对应的关系。特征匹配实际上就是计算特征向量之间二者的距离，最常用的是计算欧式距离。在进行图像特征匹配时，有Susan算法[3]、Moravec算法[4]、Forstner算法[5]等，但使用最广泛的算法是David.Lowe教授提出的尺度不变特征SIFT算法[6-7]，此算法具有相对较强的鲁棒性，当图像进行尺度大小缩放、多角度旋转、亮度变化时能够保持不变性[8]。SIFT算法在具备以上诸多优点之外，也存在容易对出现多个相似特征点共存时，出现误匹配的状况和计算复杂繁琐的缺点[9]。为了改善这些缺点，提出一种改进的SIFT算法，一方面通过降低描述子向量维度，降低计算量和复杂度；另一方面通过考虑匹配点的最近邻欧式距离，剔除误匹配点，提高特征点匹配准确度。

1 改进的SIFT算法

1.1 SIFT算法

目前，在建筑物三维重建过程中，图像特征匹配的主流算法是SIFT算法，SIFT算法实现图像特征匹配包括构建尺度空间、高斯差分、生成特征描述和特征向量匹配。

1.1.1 构建尺度空间

特征点检测是在尺度空间中完成的，从较远的地方采集建筑物的图像，尺度空间越大，图像越模糊，大尺度空间能还原建筑物表面的概貌，小的尺度空间能够还原建筑物表面的细节特征[10]。为了更详细的表示尺度空间，可以采用将图像的卷积和高斯函数二者结合进行表示

L(x,y,σ)=G(x,y,σ)I(x,y)，

(1)

式中：L(x,y,σ)——图像的尺度空间；

G(x,y,σ)——尺度空间大小可以变得函数；

σ——尺度；

I(x,y)——原始图像的尺度坐标。

1.1.2 高斯差分

为了能够提高提取尺度空间极值点的稳定性，文中采用高斯差分尺度空间(DoG)来检测部分区域的极值点。高斯差分函数为

D(x,y,σ)=(G(x,y,kσ)-G(x,y,σ))I(x,y)=

L(x,y,kσ)-L(x,y,σ)，

(2)

式中，k——放大因子。

1.1.3 特征描述子

为了保证图像在旋转时，描述子不变，首先需要定出方向参数。高斯差分尺度空间中检测出来的特征点梯度的数值以及方向计算为

m(x,y)=(L(x+1,y)-L(x-1,y))2+

(3)

(4)

特征点存在的尺度用L表示。目前，使用的SIFT算法，普遍选择以关键点为中心其邻域内16×16的窗口，在这基础上，进一步将窗口进行划分，变为16个4×4的子窗口，每个子窗口又含有8个方向的向量信息，故最终特征描述子有4×4×8共128维向量。

1.1.4 特征向量匹配

欧式距离是图像特征匹配的一个重要参数，当欧式距离小于特定阈值时，即认为匹配成功。欧式距离作为判定特征点相似度的一个重要依据，也有其局限性，当亮度发生变化时，会对欧式距离的结果造成偏差，导致匹配的准确度不高，往往结合特征向量的次近邻距离大小，来判定特征向量的相似度，整个匹配过程的公式为

(5)

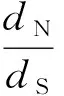
(6)

式中：dab——两特征点之间的欧式距离；

da(j)、db(j)——特征点的描述符分量；

dN——两点之间的最近邻距离；

dS——两点间的次近邻距离；

t——阈值。

在欧式距离小于给定阈值的基础上，如果dN/dS也小于给定的某个阈值t，即可认定点匹配正确。

1.2 改进的SIFT算法

为了简化计算，提高匹配的准确度，在进行特征匹配时，采用一种改进的SIFT算法。

1.2.1 描述子

描述子是用特征点周围16×16的邻域当作采样窗口，在此基础上，需要进一步划分种子区域，传统的SIFT算法种子区域有16个，每个区域内含有16个像素。文中采用的改进SIFT算法，降低描述子的采样窗口，将特征点周围15×15的像素当作采样窗口，再将窗口划分为3×3的种子区域，每个种子区域有5×5的25个像素点。

与传统的SIFT算法相比，改进的SIFT算法描述子有3×3×8的72维向量，向量维度下降率为43.75%，向量维度的降低，可以大大减小计算量和计算过程中的复杂度，改善时间性能。

1.2.2 匹配算子

传统的SIFT算法中，忽视了匹配点对的最近邻欧式距离与点对匹配正确率之间的关系。在研究了大量点对的匹配结果后，发现特征匹配正确率与dab、dN以及dN/dS有如下规律：

(1)增大图像视角，会降低特征匹配的正确率。

(2)在采集图像时，如果角度没有变化，当dab>0.4时，匹配点对的正确率几乎为0；当dab<0.4时，匹配正确率显著提升，且dab越小，匹配正确率越高。

(3)特征点匹配的准确率与dN/dS有一定的关系，即二者比值小于0.5时，匹配的准确率高；当比值大于0.5时，匹配准确率低。

结合上述三点规律，文中将dab，dN和dN/dS结合起来，作为特征点匹配准确率的依据。

在初始计算时，如果dN≥0.4，则直接舍弃该点。

若dN<0.4，开始计算dN/dS的值，并根据所得值进行讨论。若dN/dS≤0.5，则认为特征点匹配的准确率较高，将此类点归为集合A中，定义为A类点集；如果计算的比值大于0.5且小于0.8，则认为特征点匹配的准确率较低，将此类点集归为集合B中，定义为B类集合；若dN/dS≥0.8，则认为匹配错误，直接舍弃。

具体的匹配流程如图1所示。

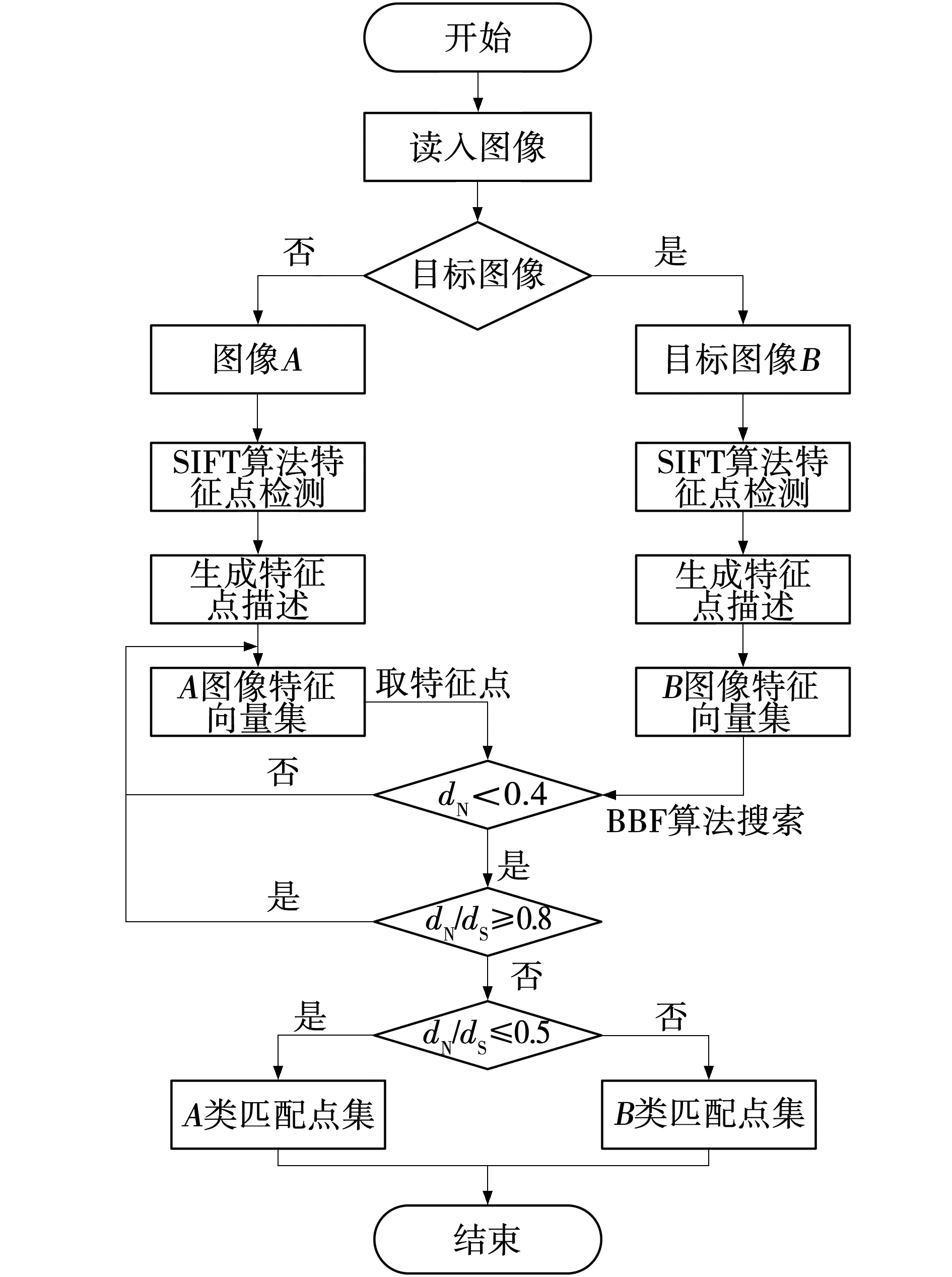
图1 初始匹配流程Fig. 1 Initial matching flow

2 实验对比分析

采用VS2018和OPENMVG搭建实验平台，配准SIFT算法与改进的SIFT算法的图像实验数据图如图2所示。采用传统的SIFT算法和文中的算法得出的结果如图3所示。

图2 实验数据Fig. 2 Experimental data graph

图3 匹配结果Fig. 3 Matching results

对两种算法的执行速度和匹配结束的效果进行对比分析，如表1和表2所示，其中初始匹配点数为n，特征点提取时间为t，初始匹配点对为m，初始匹配时间为t0，正确匹配点对为mt，误匹配点对为mf，误匹配率为e。

表1 两种算法相关运行时间对比Table 1 Comparison of relative running time of two algorithms

表2 两种算法匹配准确率对比Table 2 Comparison of matching accuracy of two algorithms

由表1可知，采用改进的SIFT算法，进行特征点提取时，所用的时间降低了46.87%，同时，初始匹配时间也降低了16.17%。节省了大量的时间，提高了匹配的效率，故改进的SIFT算法在时间性能上优于传统的SIFT算法。

由表2可知，采用传统的SIFT算法和本文改进的SIFT算法，从表2数据分析可得，采用改进的SIFT算法进行特征匹配，误匹配率减少了5.1%，匹配准确度更高。因此，改进的SIFT算法在匹配准确度上也优于传统的SIFT算法。

3 结束语

在原SIFT算法的基础上，给出了一种改进的SIFT算法进行图像特征点匹配。该算法通过减少SIFT算法描述子向量维度与改进SIFT算法匹配算子，来降低匹配过程所用的时间和提高特征匹配的准确率。通过对改进的SIFT算法和原SIFT算法的匹配结果进行分析，得出改进的算法提取特征点时，用时降低了46.87%，特征点匹配时，用时降低了16.17%，误匹配率降低了5.1%。因此，该算法在图像的特征匹配过程中具有广泛的应用价值。