高填方路堤沉降的预测方法
2020-09-24赵延林丁志刚
赵延林, 刘 旭, 丁志刚, 张 聪
(1.黑龙江科技大学 建筑工程学院, 哈尔滨 150022; 2.上海倍蒂建筑工程咨询有限公司, 上海 200000)
0 引 言
在重载铁路、山区公路及机场建设等工程中一般要进行高填方地基处理,高填方工程的工后沉降是评价工程质量的一个重要指标,目前,关于高填方工程的工后沉降预测还没有一种统一可靠的计算方法。
针对高填方工程的工后沉降预测问题,部分学者开展了相关的研究工作。叶观宝等[1]基于现场监测数据,通过第一层监测数据反演来预测下一层的沉降量,并得出了孔压系数与堆载速率之间的关系。王志亮等[2]通过对Asaoka法的研究,再进行曲线拟合,发现与实际监测拟合效果较好。刘宏等[3-4]通过各种曲线拟合与实际监测数据相结合,建立了工后沉降预测方程,并将监测数据与预测值进行对比分析,找出了最佳的沉降预测方法。姚仰平等[5-6]基于应力和时间对沉降的影响,提出了高填方蠕变实用算法。宋二祥等[7]在室内蠕变实验的基础上,提出了蠕变与干湿循环的联合计算法。邓聚龙等[8-9]通过灰色系统理论与人工神经网络模型理论,建立了沉降预测模型。
目前,高填方工程的工后沉降预测方法主要包括地基参数反演法[10]、曲线拟合法与系统理论分析法。反演法的理论和计算比较复杂,应用起来相对困难;曲线拟合法基于现场数据,考虑了各种沉降影响因素,预测结果具有较好的真实性与合理性;系统理论法过分依赖等时距数据,预测效果较差。
笔者结合实际工程的监测数据,提出一种基于双曲线模型与灰色理论模型的联合预测模型,该模型结合了两种模型的优点,以提高预测模型的计算精度。
1 工程背景
1.1 工程概况
青海公路扎龙沟至碾伯镇段长约59 km,以青海与甘肃交界处的互助县加定镇扎龙口村为线路起点,乐都区碾伯镇为线路终点,按照国家二级公路标准进行修建。路基宽度为8~10 m,设计时速60和40 km/h。该路段易发生滑坡、崩塌、泥石流等地质灾害,土类主要是季节性冻土、黄土,岩性主要为第四系粉土、碎石土、卵石等,地质条件较差,因而需要对路基进行高填方地基处理,平均回填高度30 m,回填材料为板岩。
1.2 沉降监测
扎龙沟至碾伯镇段的青海公路沉降监测是从2016年11月开始,至2017年11月结束,监测周期为1 a。此工程分5层回填,监测点按每层10 m一个点,每层布置6个监测点,纵向除最下面的一层,其余4层都要布置监测点,前两个月每月监测2次,后9个月每月监测1次。记监测天数为t,累计沉降为s最终的沉降量监测数据见表1。

表1 沉降监测数据Table 1 Settlement monitoring data
1.3 数据等时距处理
对工程中的沉降监测数据进行等时距处理,处理方法有拉格朗日插值、三次样条插值以及分段插值等方法。其中,拉格朗日插值法在每求一个新的沉降量时,都要重新计算插值函数,计算较繁琐;分段插值法是一种被分段的低次多项式插值函数,此方法光滑性较差;而三次样条插值法不仅具有二阶光滑性,而且数据处理过程简便,收敛性良好。故采用三次样条插值法对原始数据进行处理,得到的等时距监测数据见表2。

表2 等时距监测数据Table 2 Isochronous monitoring data
2 双曲线模型预测
2.1 双曲线模型
双曲线模型是结合工程沉降监测曲线进行拟合的一种沉降预测方法,它近似认为沉降值与时间成曲线函数关系。双曲线模型的基本方程为
(1)
式中:s0——t0时刻的沉降值;
st——任意时刻t时的沉降值;
t0——起始监测天数;
t——某一监测天数;
α、β——待定参数。
在式(1)中,令t-t0→ ∞,则可得出最终的沉降值为
s
(2)
2.2 模型预测分析
根据表2中的等时距沉降数据,计算各等时距对应的Δt/Δs值,应用最小二乘法,并通过Matlab软件进行编程计算,得到Δt/Δs与Δt的拟合关系曲线如图1所示,其对应的函数关系式为
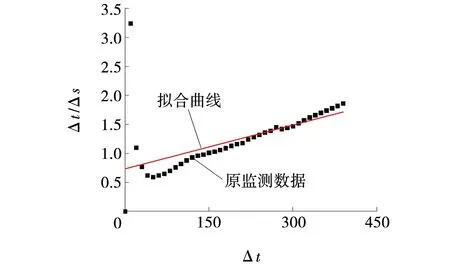
图1 Δt/Δs与Δt的拟合关系曲线Fig. 1 Relationship curve of Δt/Δs and Δt
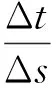
(3)
式中:Δt——某一监测天数至起始监测天数的时间段;
Δs——某一时间段对应的累计沉降值。
由式(3)得α=0.757 5、β=0.002 4,将其代入式(1),并取t0=0、s0=0,得到双曲线预测模型为
(4)
运用式(4)对0~380 d内的沉降进行预测,并将预测结果与实际监测值进行对比,如图2所示。从图2可以看出,双曲线模型的预测结果较为理想,但在第40~220 d,预测曲线与实测曲线存在一定的偏差,最大偏差为31.6%,在第320 d以后,预测曲线与实测曲线的偏差有增大的趋势。
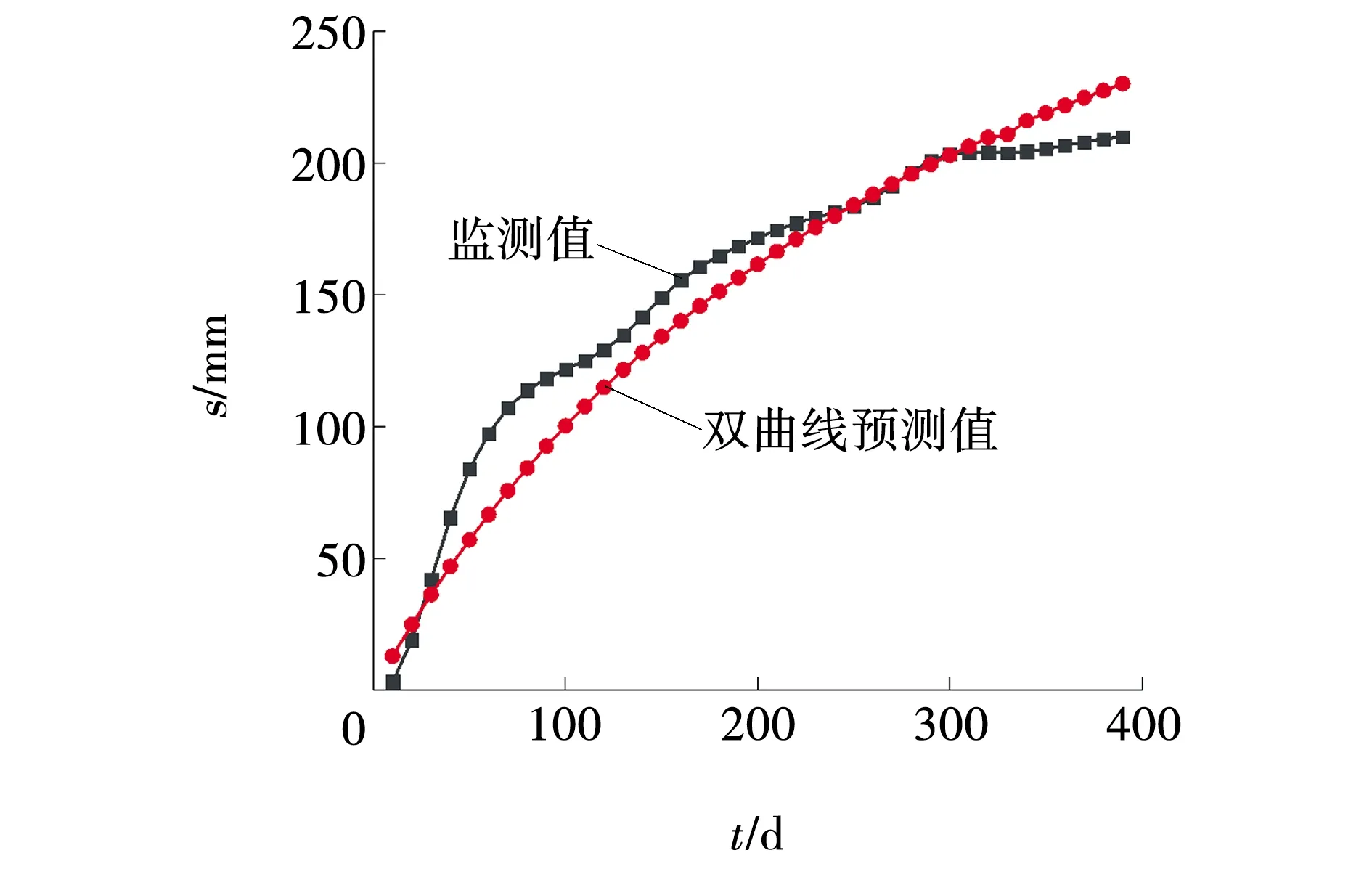
图2 双曲线预测值与实际监测对比Fig. 2 Comparison of hyperbolic prediction value and monitoring values
3 灰色理论模型预测
3.1 灰色理论模型
灰色理论模型是在少而散的数据基础上,通过提取有利的数据,使沉降数据变得规律化,进而有 效预测工后沉降的一种方法。
首先,按式(5)对工后沉降监测数据进行一次累加处理。
(5)
建立灰色微分方程为
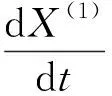
(6)
式中:a——数据发展系数;
u——数据的变化关系。
应用最小二乘法进行参数求解。
(7)
Y=[X(0)(t2),X(0)(t3),…,X(0)(tn)]T,
求解微分方程,得到沉降预测模型为
(8)
式中,k=1,2,…,n。
3.2 模型预测分析
依据表2中的等时距沉降数据,利用Matlab软件对式(5)与式(7)进行编程计算,得出灰色系统模型的计算参数为
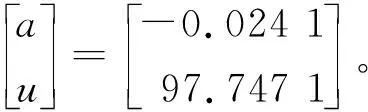
将计算参数代入式(8),得到灰色系统理论沉降预测模型为
X(1)(tk+1)==4 058.99e0.024 1k-4 055.90。
采用后验差检验法对预测模型进行精度验证,求得小概率误差P=0.973,方差比C=0.35,故模型精度为一级,可以进行预测计算。预测值与实测值的对比曲线如图3所示,由图3可知,虽然模型精度达到一级,但整体预测结果与实测结果偏差较大。
4 联合模型预测
由以上分析可知,双曲线模型对高填方工程的拟合预测效果较好,但该模型的预测精度取决于模型参数,而模型参数又取决于监测数据,因此,监测数据的优化筛选决定了双曲线模型的预测精度。灰色理论模型虽然拟合预测效果不好,但其在监测数据优化筛选方面拥有很大的优势。因此,将双曲线模型与灰色理论模型相结合,发挥各自的优势,可以有效提高预测模型的计算精度。
4.1 联合模型
应用灰色理论,按式(8)计算得出预测值X(1)={X(1)(ti)|i=1,2,…,n},按式(9)计算残差。
ε(0)(ti)=X(0)(ti)-X(1)(ti)。
(9)
按式(10)计算相对残差,并依此进行数据筛选。
(10)
设定相对残差qk值,取满足相对残差要求的连续数据作为联合预测的原始数据。在联合预测原始数据的基础上,应用双曲线模型进行沉降预测分析。
4.2 模型预测分析
结合表2的等时距沉降数据,应用灰色理论模型进行数据筛选,按式(8)~(10)计算残差与相对残差为
ε(0)(ti)=(0,-80.50,-59.55,-38.53,-22.58,
-11.58,-4.59,-0.67,1.11,1.70,2.02,
3.02,5.56,9.42,13.96,16.91,18.74,19.35,
19.26,18.87,18.20,17.06,15.28,13.16,
11.32,10.32,10.62,11.46,11.33,9.14,
5.12,0.21,-4.85,-9.47,-13.69,-17.76,
-21.90,-26.34,-31.31),
qk=(0,-4.250,-1.420,-0.590,-0.270,-0.120,
-0.040,-0.010,0.010,0.010,0.020,0.020,
0.040,0.070,0.090,0.100,0.100,0.100,
0.100,0.100,0.110,0.100,0.090,0.070,
0.060,0.060,0.060,0.060,0.060,0.050,
0.030,0.001,0.020,-0.050,-0.070,-0.090,
-0.110,-0.130,-0.150)。
设定相对残差qk值为(-0.1,0.1),从相对残差计算结果可知,70~200 d或210~360 d数据可作为最优原始数据,这里选取70~200 d的监测数据作为最优原始数据。通过最小二乘法,应用Matlab软件拟合出Δt/Δs与Δt的关系曲线如图4所示,其函数表达式为
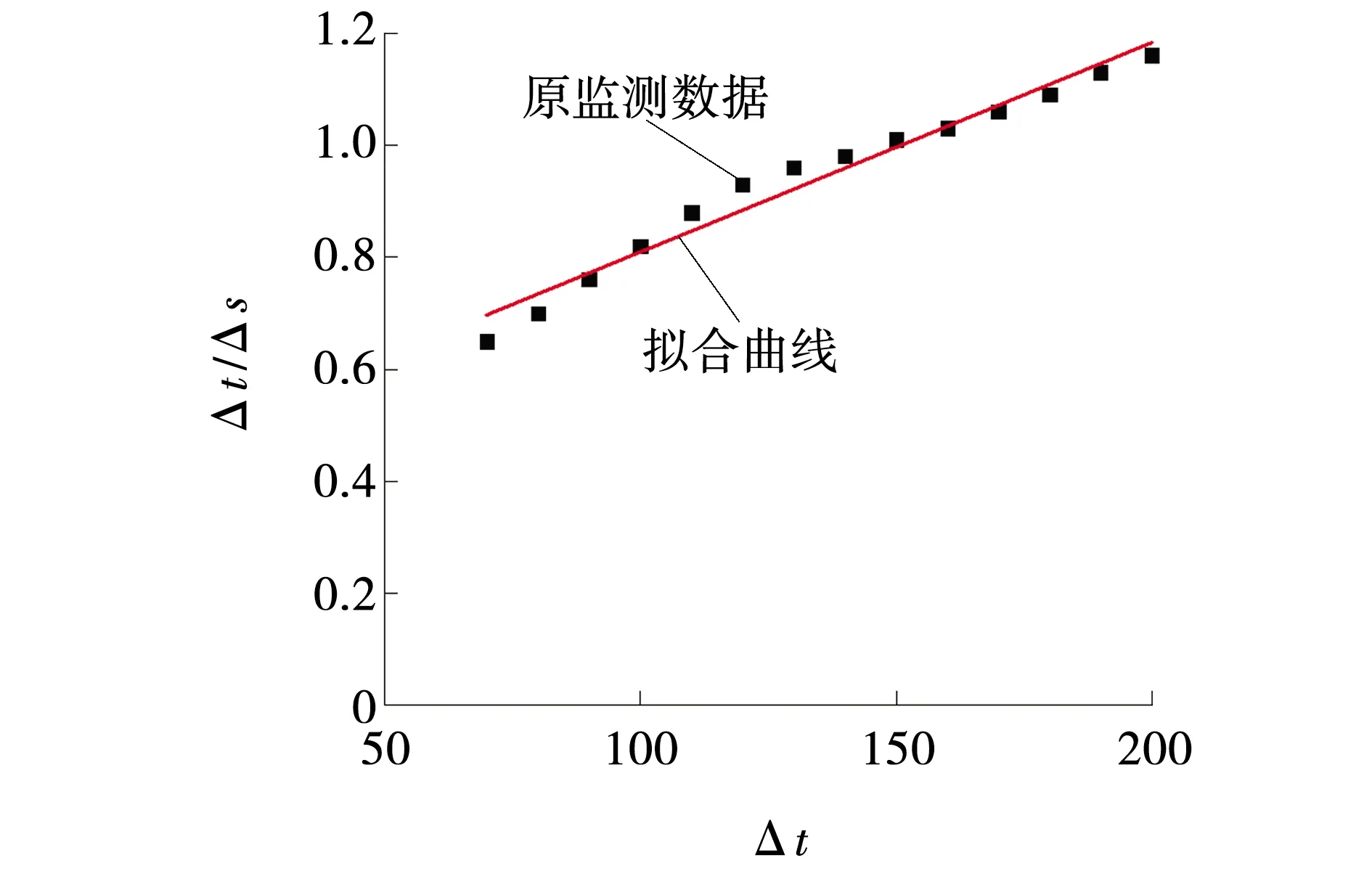
图4 Δt/Δs与Δt的拟合关系曲线Fig. 4 Relationship curve of Δt/Δs and Δt
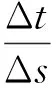
(11)
由式(11)可知,双曲线模型参数α=0.435 0,β=0.003 7。
取s0=3.09、t0=10,建立沉降预测模型为
按此模型对沉降数据进行预测,并将预测结果与监测数据、双曲线模型及灰色理论模型预测结果进行对比,如图5和图6所示。
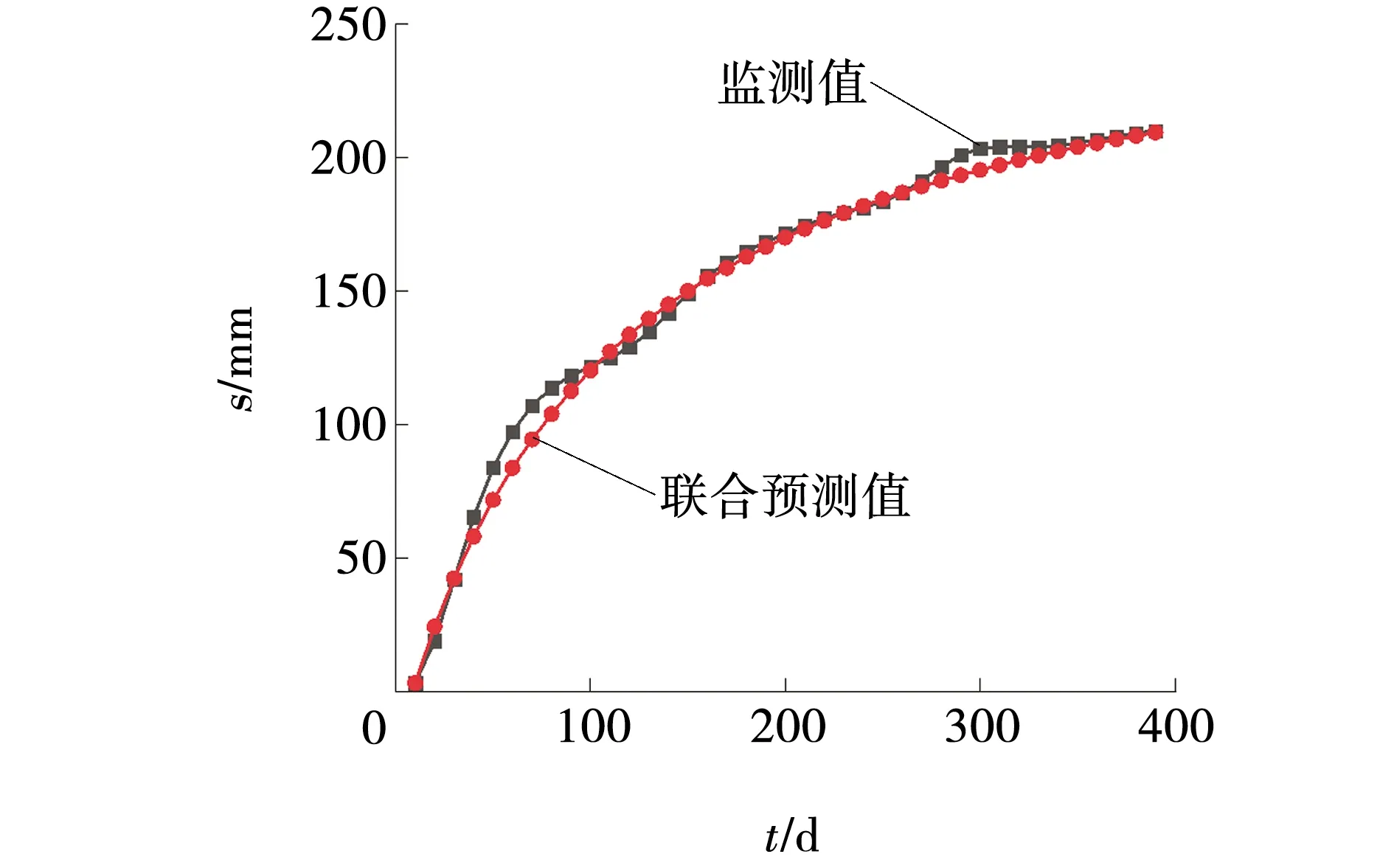
图5 联合模型预测值与监测值对比Fig. 5 Comparison of joint model prediction values and monitoring
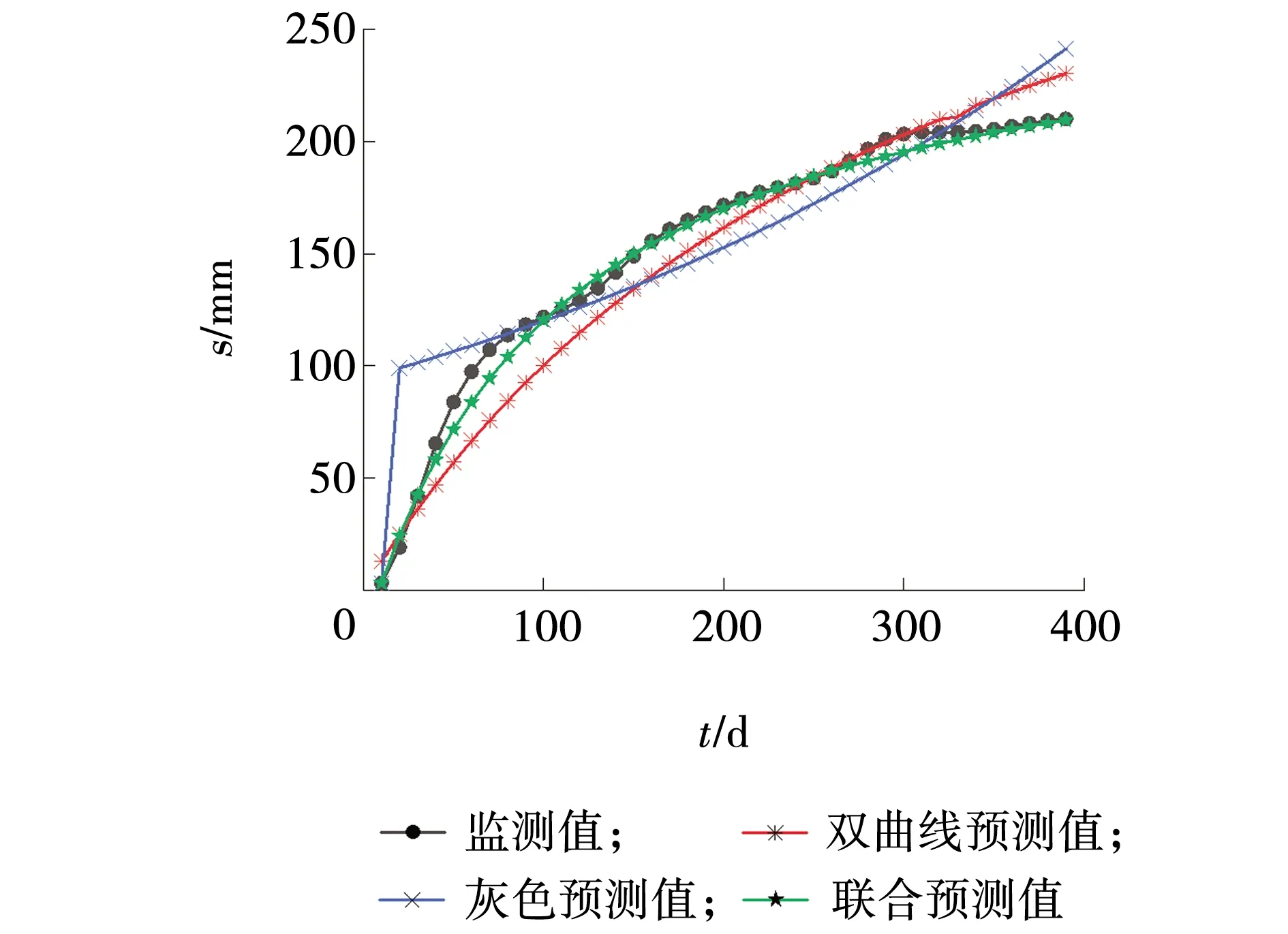
图6 各模型预测值与监测值对比Fig. 6 Comparison of each model prediction values and monitoring values
由图5、6可知,联合模型预测结果与监测数据拟合效果非常好,整体预测情况稳定,预测结果与监测数据的局部最大偏差仅为12.7%,与双曲线模型预测结果相比,整体预测精度有较大幅度的提升。
5 结 论
(1)双曲线模型的预测结果较为理想,但其预测精度取决于监测数据的优良性,当存在不良监测数据时,双曲线模型的预测精度会受到较大的影响。
(2)灰色理论模型的预测结果较差,但其在监测数据优化筛选方面拥有较大的优势。
(3)基于双曲线模型与灰色理论模型的联合模型可以充分利用两种模型的优点,大幅度的提高了工后沉降的预测精度。
