一种云存储完整性的格签名验证方法

常 亮， 王冠棋， 杨雪欣

(黑龙江科技大学 计算机与信息工程学院， 哈尔滨 150022)

云存储系统可以使用户以低廉的价格获取海量的存储能力，但数据的高度集中同样使其面临着严峻的安全挑战。当用户选择云存储模式时，用户一般并不会在本地保存数据副本。换言之，用户可能失去了对这些数据的物理控制。这些存储在云端的数据不仅可能会遭受来自其他用户的恶意攻击，甚至还可能遭到不可靠云服务提供商(Cloud storage service provider,CSP)的滥用，如窥视用户隐私、挖掘用户隐私、数据丢失瞒报、数据恶意篡改等。随着量子计算技术的发展，大素数因子分解难题和有限域上离散对数问题将变得不再困难，基于传统难题的RSA、DSA、ECDSA等签名方案也面临失去安全的风险。大数据时代为保证用户数据的安全性和完整性，迫切需要对传统数据完整性验证方案加以多方面更加安全的改进。为此，笔者提出了一种基于格的云存储完整性验证方法，通过效率分析和安全分析来验证其性能。

1 基本原理

1.1 PDP数据完整性验证方案

数据持有性证明方案(Provable data possession,PDP)采用随机抽样的策略，概率性的进行数据完整性验证。这是一个静态的基于RSA签名同态特性的概率性策略，进而开创了在不可信存储器上的数据完整性验证方案。典型PDP方案的逻辑架构如图1所示。

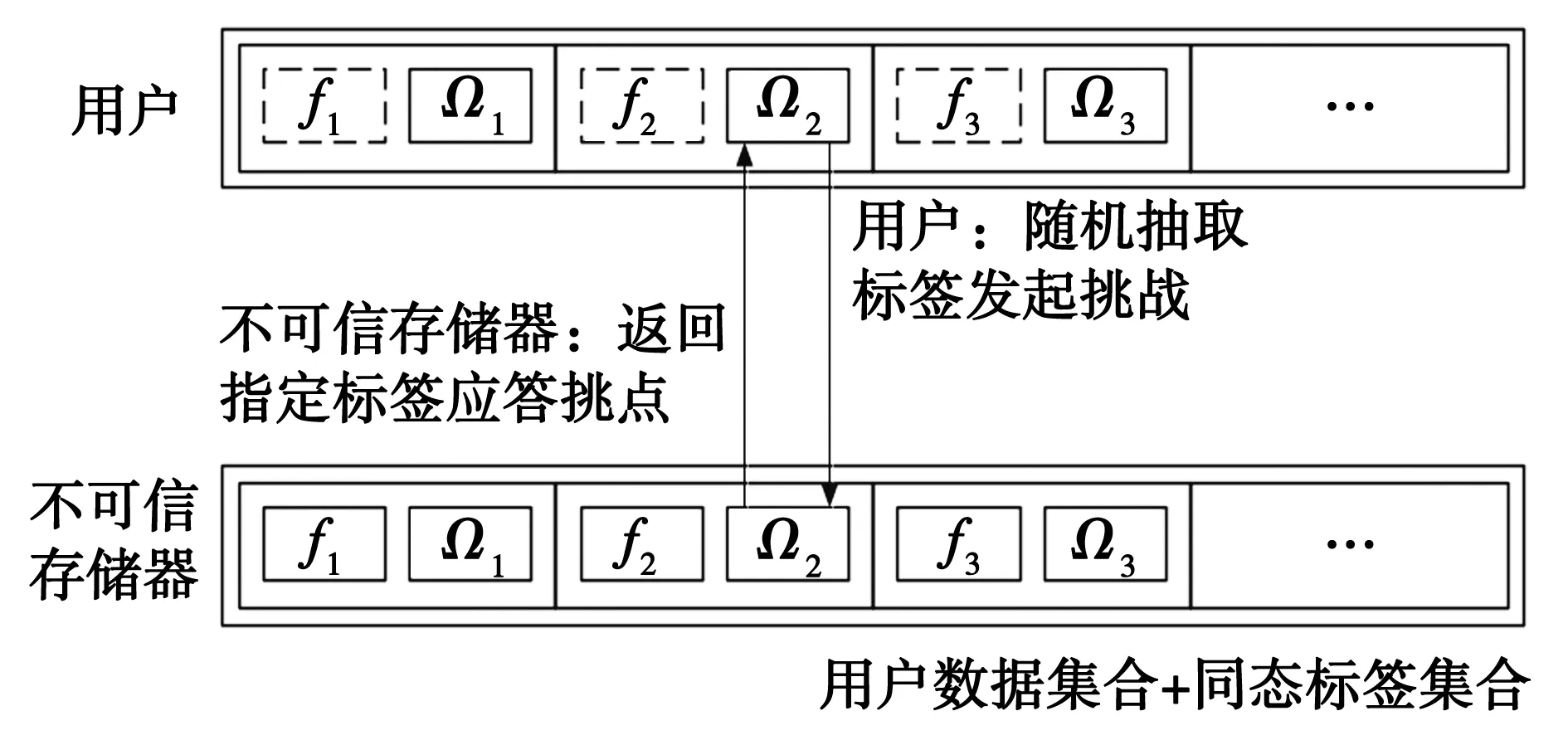
图1 PDP方案的基本架构Fig. 1 Basics PDP scheme architecture

1.2 格和格难题

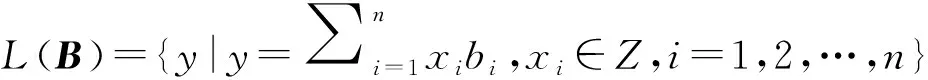
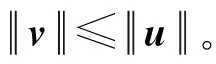
1.3 LWE问题

容错学习(Learning with errors，LWE)是格密码学的基础问题，其困难性可以归约成格的SVP和SIVP问题。LWE问题包括CLWE(LWE搜索)问题和DLWE(LWE判定)问题。

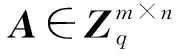
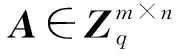
1.4 同态签名

设签名者所持有的公钥为pk，私钥为sk，对数据块m而言，分别对其任意数据子块m1、m2做对应的签名得σ1、σ2。若签名方案满足以下性质：

不可伪造性。只有持有密钥对(pk,sk)的签名者才能生成签名σ。

验证简化性。已知签名σ1、σ2，任取随机数k1、k2对数据块m′=k1m1+k2m2而言，验证者可以在不知道m1、m2的情况下，通过σ1、σ2和k1、k2计算并对数据块m′进行验证。

非扩展性。已知签名σ1、σ2，任取随机数k1、k2，对应的数据块m′=k1m1+k2m2而言，验证者在不持有私钥sk的前提下，无法通过线性结合的方式生成新的满足验证条件的签名σ′，则称该签名方案为一个同态签名方案，该签名为同态签名[3-4]。

公钥同态加密方案，一般由3个多项式时间算法构成。

(1)密钥生成KeyGen(1λ)→(pk,sk)：输入安全参数λ、输出公钥pk、私钥sk。

(2)明文加密Enc(m,pk)→c：输入明文m、公钥pk、输出密文c。

(3)密文解密Dec(c,sk)→m：输入密文c、私钥sk、输出明文m。

1.5 Merkel散列树

Merkle散列树(Merkle hash tree, MHT)是一种树形数据结构，可以花费较短的开销进行数据验证，其被广泛应用于云存储、P2P、比特币等需要进行快速验证的领域[5]。其叶子节点存储各个数据子块的哈希值，非叶子节点存储其子节点值之和的哈希值[6]。

当用户端对服务器端数据某个数据子块进行完整性验证时，服务器端返回Merkel树上对应数据子块的叶子节点存储的哈希值和相对的直至Merkel树根节点的辅助路径上的哈希值[7]。用户端只需对所返回叶子节点存储的哈希值和所返回辅助路径上的哈希值进行简单计算，并与用户端所持有的原数据块的哈希值进行对比，即可判定原数据块和对应数据子块的完整性[8]。

2 系统模型

2.1 基本结构

云存储数据完整性验证模型由三方组成：用户、云服务器提供商和第三方审计者[3]，如图2所示。

在上述三方架构模型中，用户首先对第三方审计者发起委托验证请求[9]。第三方审计者收到用户的委托验证请求，根据用户的委托验证请求生成相应的挑战信息，对云服务提供商发起相应的挑战-应答游戏请求,然后云服务提供商响应第三方审计者所发起的挑战，进行数轮挑战-应答游戏[10]。最后第三方审计者根据数轮挑战-应答游戏的结果，得到对应的用户数据完整性证明结果，并将该完整性证明返回给用户。

2.2 基本算法

基本算法主要由5个多项式时间算法组成，如图3所示。

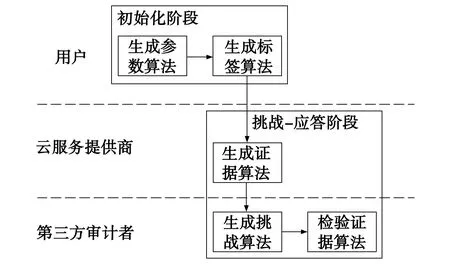
图3 基本算法流程Fig. 3 Basic algorithm model

(1)生成参数算法KeyGen，由用户执行，算法输入随机长度{0,1}串，输出公私钥对(pk,sk) 。

(2)生成标签算法Encode，由用户执行。算法输入公私钥对(pk,sk)和数据子块m，输出对应标签对Tm。

(3)生成挑战算法Challenge，由第三方审计者执行。算法输入待检测数据子块集合I(由TPA随机产生)，输出对应挑战信息chal。

(4)生成证据算法Prove，由云服务提供商执行。算法输入挑战信息chal，输出对应证明信息proof。

(5)检验证据算法Verify，由第三方审计者执行。算法输入证明信息proof，输出证明结果{0,1}。当证明信息有效时，即用户数据完整性得到证明时，输出1。反之，输出0。

3 验证方案

3.1 验证步骤

(1)初始化阶段。用户执行密钥生成算法KenGen，生成公钥pk、私钥sk。用户将所持有原数据块F分成若干个数据子块f，并执行明文加密算法Enc，对每个数据子块f用公钥pk加密，生成每个数据子块的验证标签。用户保存私钥sk，以执行密文解密算法Dec，对每个由数据子块生成的验证标签加以验证。根据各个数据子块f[i]所对应的数据子块签名σ[i]，自底至顶建立Merkel树，最终求得根节点的哈希值hr。随后，用户将各个数据子块f[i]和其对应的数据块签名σ[i]发送至CSP，并删除本地数据。

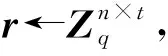
密文解密算法Dec,密文解密者对所接收密文C=(c1,c2)和所持有私钥sk=s，计算M′=c2-c1⊙sk=r⊙(A⊙s+e)+msg-(r⊙A)⊙s，以及M=M′mod2。由于随机误差项矩阵e是由服从离散高斯分布的偶数元素所构成，故模2操作后得到最终解密后的明文M=msg。

(2)挑战阶段。用户委托TPA周期性的对CSP发起完整性验证挑战。当用户委托TPA对CSP发起完整性验证挑战时，用户将欲校验数据完整性的数据子块的唯一标识符id和其对应签名Sig(id)作为审计请求发送至TPA。当TPA接收到用户发送的审计请求时，通过验证签名的方式来判断该请求是否来自合法用户。当确认用户合法后，TPA发起挑战。TPA随机抽取c个元素构造数据块索引集合I={s1,s2,…,sc}并将其发送至CSP，其中c∈[1,n]。

(3)应答阶段。当CSP接收到TPA发送的挑战信息后，自底置顶建立Merkel树。CSP根据数据块索引集合I={s1,s2,…,sc}寻找数据块所对应的叶子节点，并寻访该叶子节点至Merkel哈希树根节点的路径上所有兄弟节点，将其记录为对应的辅助路径集合{Ωi}，其中i∈{s1,s2,…,sc}。最后，CSP将数据块所对应的叶子节点签名Sig(ci)和辅助路径集合{Ωi}作为证据σ={Sig(ci),Ωi}返回给TPA。

(4)验证应答阶段。当TPA接收到CSP返回的验证证据σ={Sig(ci),Ωi}，i∈{s1,s2,…,sc}时，利用叶子节点签名Sig(ci)和辅助路径集合{Ωi}，计算对应的Merkel树根节点值。如果用户签名Sig(ci)通过公钥pk验证成功，并能通过叶子节点签名和辅助路径集合生成Merkel树根节点值，则证明用户数据完整性未被破坏。反之，则证明用户数据完整性遭到破坏。

3.2 正确性与安全性

当验证者持有私钥sk=s时，有c′=c2-c1⊙sk=c2-c1⊙s=r⊙(A⊙s+e)+msg-(r⊙A)⊙s，因⊙是环R上的同态运算，其满足结合律，故有c′=r⊙A⊙s+r⊙e+msg-r⊙A⊙s=r⊙e+msg。

因随机误差项e是n×t个偶数元素，加密消息msg是{0,1}的消息串，故做模2操作后，可得r⊙e=0，即c′=0+msg=msg，等式c′=msg成立，签名正确性得证。

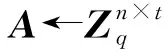
(3)挑战应答正确性。当用户数据块m=(m1,m2,…,mn)中任一数据子块mi遭到破坏时，其对应签名Sig(mi)也遭到破坏。因哈希函数具有单向性和抗碰撞性，故而CSP自底置顶建立的Merkel哈希树的根节点值root′与TPA所持有的哈希树根节点值root不可能一致。root′≠root不成立，挑战应答正确性可证。

3.3 效率分析

针对所提出的基于格的数据完整性验证方法进行仿真效率分析，选择数据子块大小为4 kB，数据子块总数n=100 000，选取基于BLS签名方案和ECDSA签名方案的数据完整性验证方案，作为参照对比。重复进行50次仿真实验，将结果取平均值，效率对比结果如表1所示,其中，参数生成开销为tc，签名开销为tq, 挑战-应答开销为tt。

表1 数据完整性验证方案开销对比Table 1 Parameters of experimental cost for different data integrity verification

4 结束语

结合格签名和Merkel树的数据完整性验证方法，其具有相对效率优势。该方法的高效性体现在格签名计算基于线性运算，优于基于BLS短签名和基于ECDSA椭圆曲线签名的模指数运算和对数运算，减少了签名的运算量，在参数生成开销和签名生成开销方面具有一定优势。该方法的安全性体现在格签名基于LWE困难问题，同时具有一定的抗量子攻击性，但较其他方案而言，仍存在密钥复杂时计算困难等问题，优化密钥长度和改进环R上同态运算还需要进一步研究完善。