低扬程水泵装置停泵过渡过程Simulink仿真

丁 聪

(上海勘测设计研究院有限公司，上海 200434)

1 概述

我国沿江滨湖地区已建许多大型低扬程泵站。停泵过渡过程的研究是大型轴流泵、泵装置、泵站重要研究内容之一[1-2]。泵站在起动、停机等水力瞬变过程中常出现最不利工况，在运行安全可靠性方面出现问题，因此，停泵过渡过程的计算是校核泵组运行安全性的重要内容。低扬程泵装置停泵动态特性计算需分析确定机组转动力矩平衡方程、流道的非恒定流方程、闸门水力损失表达式，并合理的引入水泵的全特性，最终建立停泵过渡过程的数学模型[3]。水泵的全特性较为复杂，为方便计算，可利用无因次新坐标参数化得到的Suter特性曲线。为有效减少Suter特性曲线拟合取值误差，可使用较成熟的移动最小二乘法进行特性曲线的拟合插值[4]。

建立的停泵过渡过程的数学模型为微分方程组，因此，停泵过渡过程的仿真求解实质为解微分方程。Matlab中的Simulink采用模块化思路搭建数学模型，可方便进行微分方程的求解，并较容易修改模块参数。因此，本文拟利用Simulink进行低扬程水泵装置停泵过渡过程的仿真计算。

2 停泵过渡过程数学模型建立

2.1 机组转动力矩平衡方程

停泵过渡过程中，低扬程泵机组的转动力矩平衡方程为[5]：

(1)

式中GD2为回转部分的飞轮力矩；n为机组转速；Mz为的阻力矩，包括水泵水力矩、水泵惯性附加力矩、泵组摩擦力矩、风阻力矩。

由于泵组摩擦力矩及风阻力矩较小，可忽略不计，仅考虑水泵水力矩、水泵惯性附加力矩。

水泵水力矩为水泵固有特性，详见2.3节。水泵惯性附加力矩可使用下式计算。

(2)

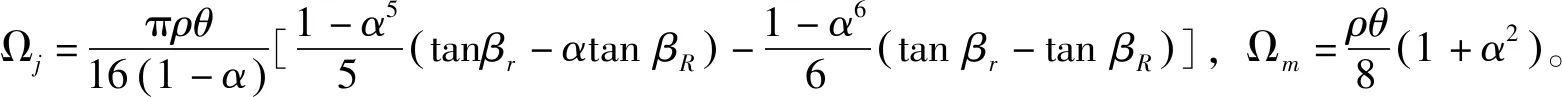
其中θ为泵叶片平面包角；α为泵叶轮轮毂比；βr为根部翼型安放角；βR为外缘翼型安放角。

2.2 水头平衡方程

低扬程水泵装置停泵时流道为满水状态。取进、出水池两个断面，依据伯努利方程可得：

(3)

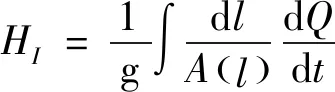
水头平衡方程可简写为[6]：

(4)

式中Hsta为出、进水池水位差，Hsta=Z2-Z1。

2.3 水泵水力特性

低扬程水泵装置停泵过程中水泵必然经历水泵工况、泵制动工况、水轮机工况。数值模拟停泵过渡过程必然要使用水泵的全特性曲线。水泵全特性曲线是以流量为横坐标、扬程和转矩为纵坐标绘制不同转速下的四象限特性曲线；或以相对速度为横坐标、相对流量为纵坐标，以两簇等相对扬程和等相对转矩曲线表示的性能关系。水泵全特性曲线形式比较复杂，不便于数值计算时使用。

Suter、Marchal和Flesh[7]根据泵的相似原理，提出x=π+arctan(v/β)、WH(x)=h/(β2+v2)、WB(x)=m/(β2+v2)新体系，将水泵全特性曲线变换为2条无因次曲线。

(5)

式中h=H/HN，β=n/nN，v=Q/QN，m=M/MN，为水泵扬程、转速、流量、转矩无量纲量。

由于停泵过渡过程中水泵特性连续变化，因此，为保证模拟精度需使用实测的连续的水泵性能曲线。但试验所得的特性曲线也均为离散点，若直接采用离散点插值计算，会大大降低模拟精度。移动最小二乘法(MLS)是一种基于点的近似方法，具有拟合精度高、通用性强的特点。因此，为较好地使用已知Suter特性曲线，使用移动最小二乘法(MLS)对Suter特性曲线进行拟合，其基本原理如下[8]。

设待求函数u(x)在域Ω内个节点xI(I=1，2，…N)处数值已知，即uI=u(xI)。计算点x的域Ωx内函数u(x)的函数uh(x)可项式表示为：

(6)

其中p(x)为式基向量，a(x)为向量，m代的项数。通常选取单项式作为基函数，此处选择二次基函数，即m=3，pT(x)=[1，x，x2]。LS是通过令uh(x)与节点的函数值uI之加权平方和最小构造近似函数，即使下式取最小值。

(7)

其中n为点x的求解域Ωx内含的节点数。w(x-xI)为点xI相权函数，此处取高斯函数。令：

W(x)=diag(w1(x)，w2(x)，…，wn(x))，

wi(x)=w(x-xi)，

B(x)=pTW(x)，

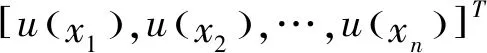
由式(7)取最小值解得系数向量a(x)。

a(x)=A-1(x)B(x)u

(8)

将式(8)代入式(6)中得：

uh(x)=∅(x)u

(9)

2.4 闸门关闭特性数学模型[9]

水流经过快速闸门属于淹没孔口出流，则流量可表示为：

(10)

式中k为闸门相对开度，k=Ak/Az=(t0-t)/t0，t0为全关需要时间，Ak为开启面积；Az为面积；μ为流量系数，μ=0.6-0.176e。

闸门的水头损失可表示为：

(11)

式中ζz为局部损失系数，ζz=1.2(k-2.63-1)。

2.5 停泵过渡过程数学模型

结合式(1)(2)(5)可得机组转动力矩平衡综合方程：

(12)

结合式(4)(11)可得停泵水头平衡综合方程：

(13)

3 停泵过渡过程Simulink模型搭建

Matlab软件的Simulink提供了各种数学模块，仅需根据仿真需要将不同模块组合搭建即可。但Simulink模块搭建有其自有的规则。为方便停泵过渡过程数学模型的搭建，需将式(12)进行变形。

(14)

根据停泵过渡过程数学模型表达式(13)(14)，搭建停泵过渡过程模型原理图(见图1所示)。

图1 停泵过渡过程模型原理示意

根据停泵过渡过程模型原理图在Simulink中进行模块搭建，搭建仿真模块如图2所示。

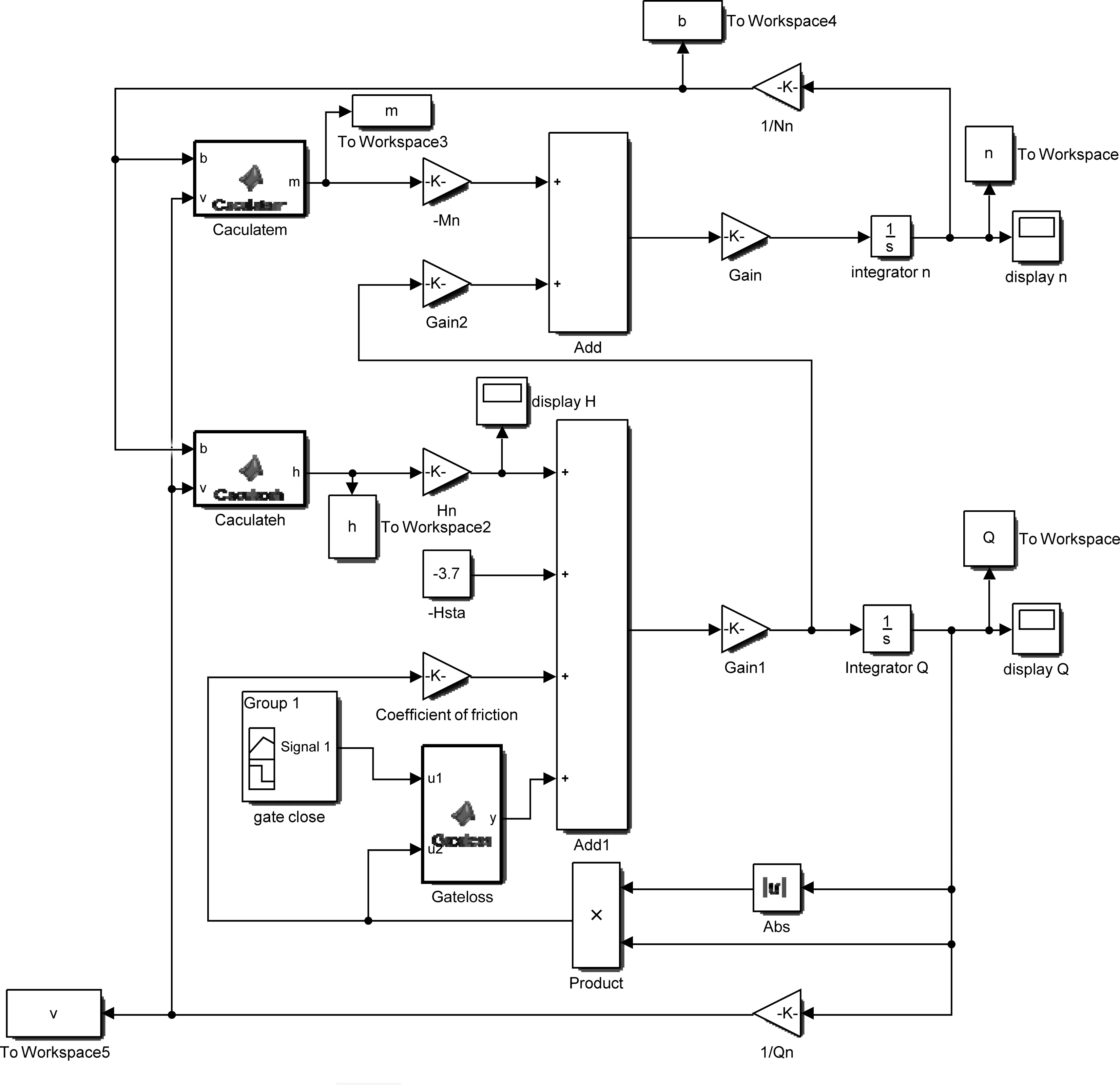
图2 停泵过渡过程Simulink模块示意

由于Suter特性曲线以流量、转速的无因次量为横坐标，而计算中需利用Suter特性曲线求取水泵扬程、转矩。因此，可理解为给定流量、转速，求取扬程、转矩，如此可利用Simulink模块中的自定义MATLAB Function进行计算，并可将移动最小二乘法(MLS)对Suter特性曲线拟合计算内置其中。

4 停泵过渡过程动态特性

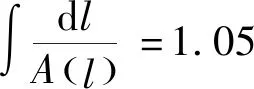
根据上述资料，计算得数学模型中的各项系数如下：

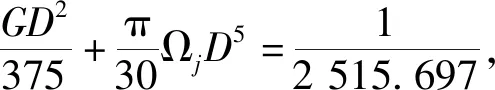
图3 闸门未关闭停泵过渡过程示意

在正转正流、正转逆流阶段，泵的流量、转速下降急剧，2.63 s左右泵开始倒流，转速降至0.423nN；85 s左右泵开始倒转，反转流量为0.769QN；泵组趋于稳定时反转流量为1.552QN，转速为1.426 8nN，转速已超反转1.2倍要求。因此，泵站停泵时需配备事故闸门，闸门应做到快速关闭。

考虑闸门关闭，假设闸门线性关闭，20 s内全部关闭，仿真计算的结果如图4所示。

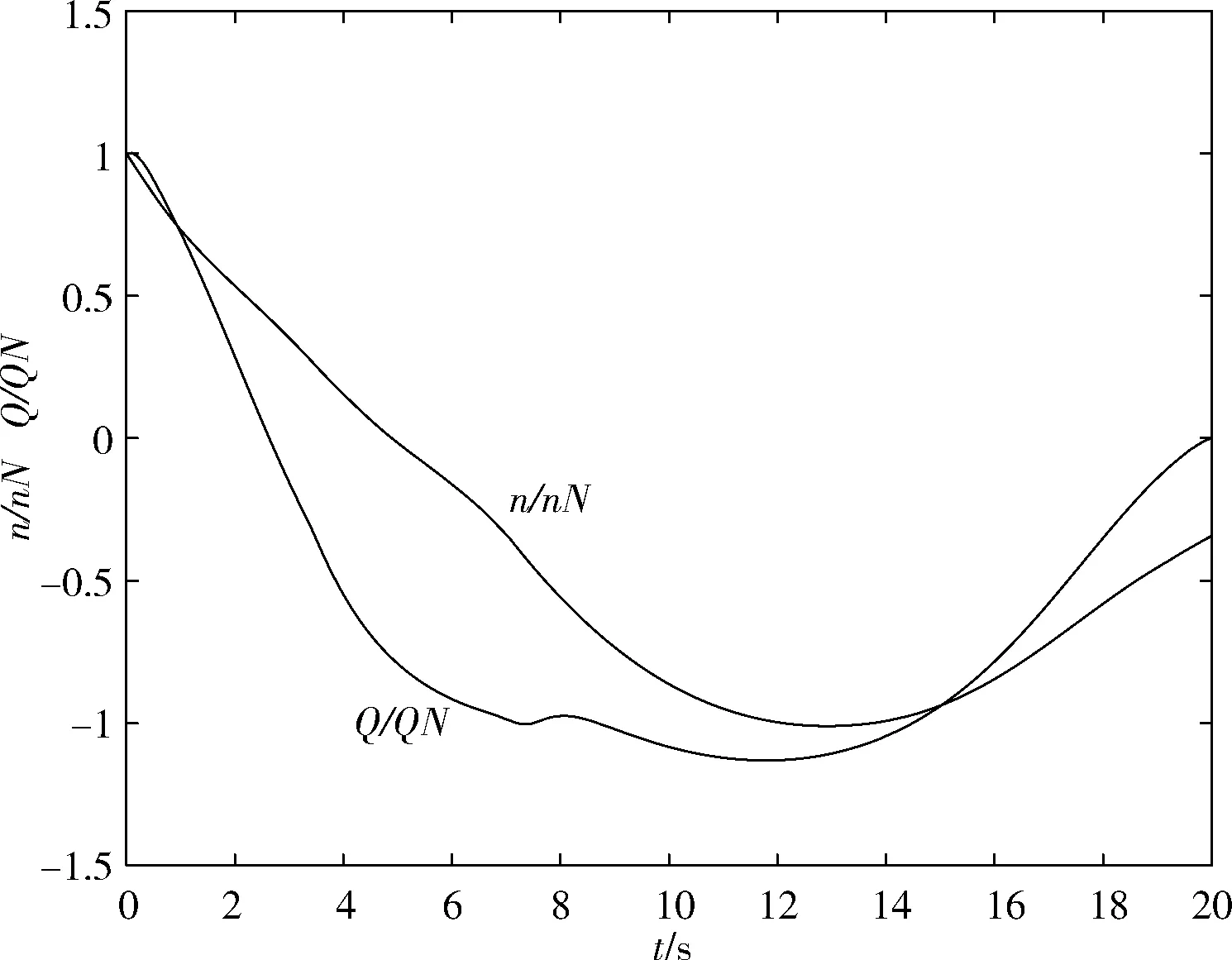
图4 闸门线性关闭停泵过渡过程示意

由于停泵初期闸门关闭较小，泵的流量、转速下降急剧。2.63 s左右泵开始倒流，转速降至0.423nN；85 s左右泵开始倒转，反转流量为0.761QN。但随着闸门孔口的减小，泵组反转流量、反转转速下降速度减缓，并开始减小，最终将趋于0流量和0转速。

若计算闸门不同关闭规律下的泵站停泵过渡特性，仅需对gate close模块进行修改。若想更换水泵叶轮，只需将MATLAB Function模块中的水泵Suter特性曲线进行更换。若模拟其他泵站的停泵过渡特性，仅需修改相应的水泵物理参数、流道特性参数以及泵站基本水位特性。由此可见，仅需简单修改Simulink模型中的模块参数便可完成不同闸门关闭规律的停泵特性计算，以及其他新工程的模拟计算。

5 结语

本文分析确定了低扬程水泵装置停泵过渡过程的机组转动力矩平衡方程、流道的非恒定流方程、闸门水力损失表达式，并采用移动最小二乘法，较合理地拟合了水泵Suter特性曲线。然后使用Simulink模块化搭建了泵站停泵过渡过程模型，并模拟了闸门未动作和闸门动作时的停泵特性。通过模型搭建及模拟计算可以发现，Simulink模块可方便搭建泵站停泵数学模型，并且简单修改模块参数，便可比较方案的合理性和完成新工程的计算。Simulink可方便地将模拟计算通用化。